Função horária da velocidade e da aceleração do MHS
Exercícios de vestibulares com resolução comentada sobre
Função horária da velocidade e da aceleração do MHS
1-(UFB) A função horária da elongação de uma partícula em MHS é x = 4.cos(p + pt) SI.
a) a função horária da velocidade
b) a velocidade máxima e a velocidade mínima
c) o gráfico da velocidade em função do tempo
d) a função horária da aceleração
e) a aceleração máxima e a aceleração mínima
f) o gráfico da aceleração em função do tempo
g) o gráfico da aceleração a em função da elongação x
2-(UFCE) A figura a seguir mostra uma partícula P, em movimento circular uniforme, em um círculo de raio r, com velocidade angular constante w, no tempo t = 0.
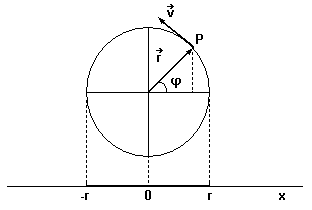
A projeção da partícula no eixo x executa um movimento tal que a função horária vf(t), de sua velocidade, e expressa por:
a) vf(t) = w r
b) ) vf(t) = w r cos (wt + j)
c) vf(t) = – w r cos (wt + j)
d) vf(t) = – w r sen (wt + j)
e) ) vf(t) = w r sen (wt + j)
3-(UFPB) Uma partícula material executa um movimento harmônico simples (MHS) em torno do ponto x = 0. Sua aceleração, em função da posição, é descrita pelo gráfico a seguir.
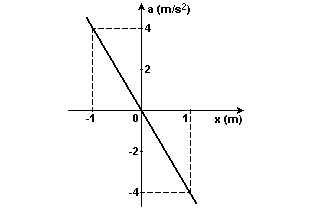
Nessas condições, a freqüência angular do MHS é:
a) 4 rad/s
b) 3 rad/s
c) 2 rad/s
d) 1 rad/s
e) 0,5 rad/s
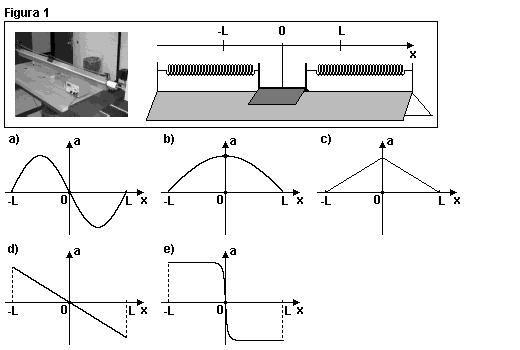
4-(UFF-RJ) Medidores de tempo são, em geral, baseados em osciladores periódicos. Um exemplo mecânico simples de um desses osciladores é obtido com um carrinho, preso a duas molas ideais, que oscila, sem atrito, entre as posições x = ± L em torno da sua posição de equilíbrio x = 0, conforme ilustrado na figura 1.
Assinale o gráfico que melhor representa a aceleração do carrinho em função da sua posição x.
5- (MACKENZIE-SP) Um disco de 20cm de diâmetro gira uniformemente em torno de um eixo O, sobre um plano horizontal executando 60rpm. Perpendicularmente ao plano do disco, existe um anteparo, conforme figura.
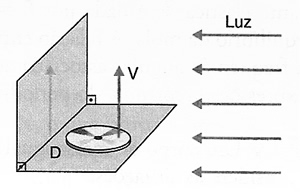
Ao fixarmos um objeto cilíndrico de pequeno diâmetro. Perpendicularmente ao disco, num ponto de sua periferia, o mesmo passa a descrever um MCU de freqüência igual a do disco Pede-se a máxima velocidade da sombra do objeto.
6-(MACKENZIE-SP) Uma partícula em MHS tem velocidade máxima 2,0pm/s. Se a amplitude do movimento é 20cm, seu período é de:
![]()
7-(PUC-SP) A figura abaixo representa uma senóide para t>0, indicando a velocidade do ponto P móvel na trajetória (0,x), em função do tempo.
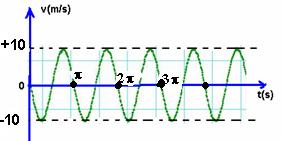
a) sua velocidade inicial e sua fase inicial
b) sua pulsação (velocidade angular) e sua amplitude
c) a maior distância que ele alcança da origem
d) a aceleração máxima por ele adquirida
8-(UFCE) Um carrinho desloca-se com velocidade constante, vo, sobre uma superfície horizontal sem atrito, conforme figura.
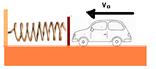
O carrinho choca-se contra uma mola de massa desprezível, ficando preso a ela. O sistema mola+carrinho começa então a oscilar em movimento harmônico simples, com amplitude de valor A. Determine o período de oscilação do sistema.
9-(Fuvest – SP) Dois corpos, A e B, ligados por um fio, encontram-se presos à extremidade de uma mola e em repouso. Parte-se o fio que liga os corpos, e o corpo ![]() passa a executar um movimento oscilatório, descrito pelo gráfico abaixo:
passa a executar um movimento oscilatório, descrito pelo gráfico abaixo:
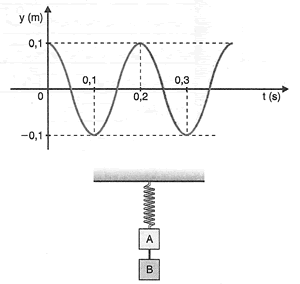
a) Determine a frequência, a amplitude e a pulsação do movimento de A.
b) Escreva a equação horária das posições Y do corpo A, conforme o gráfico.
10-(UNESP-SP) Um móvel com MHS obedece à função horária x=7.cos(p/2.t), onde x é medido em centímetros e ![]() em segundos. Calcule:
em segundos. Calcule:
a) O tempo necessário para que este móvel vá da posição de equilíbrio para a posição de elongação máxima.
b) A velocidade máxima e a aceleração máxima
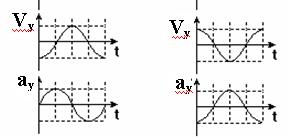
11-(UFMS) A figura 1 representa um sistema mecânico que ilustra o funcionamento de um motor a combustão, simplificado, com apenas três peças: virabrequim, biela e pistão. Essas três peças estão acopladas entre si, através de eixos articulados. Enquanto o virabrequim gira com velocidade angular constante, no sentido horário, a biela faz o pistão subir e descer num movimento oscilatório. A posição do pistão no eixo vertical y, é dada pela projeção do ponto de articulação entre a biela e o pistão sobre esse eixo.
Essa posição no eixo y, oscila entre as amplitudes +A e -A.
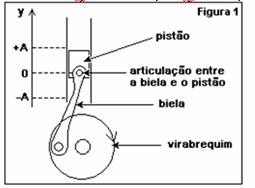
Chamemos de y, vy e ay, respectivamente, a posição, a velocidade e a aceleração do ponto de articulação entre a biela e o pistão.
Se iniciarmos a marcação do tempo t, quando a posição do ponto de articulação entre a biela e o pistão estiver na posição y = 0, como mostra a figura 1, assinale a alternativa que apresenta corretamente os gráficos correspondentes às posições y, às velocidades vy e às acelerações ay em função do tempo.
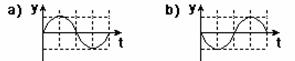
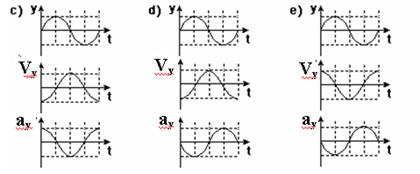
12-(UFPR-PR)
A peça de uma máquina está presa a uma mola e executa um movimento harmônico simples, oscilando em uma direção

horizontal. O gráfico a seguir representa a posição x da peça em função do tempo t, com a posição de equilíbrio em x = 0.
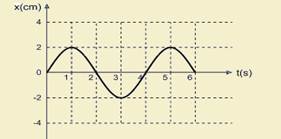
Com base no gráfico, determine:
a) O período e a frequência do sistema peça-mola.
b) Os instantes em que a velocidade da peça é nula. Justifique a sua resposta.
c) Os instantes em que a aceleração da peça é máxima. Justifique a sua resposta.
