Associação de molas – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Associação de molas

 

1- Período T da mola da figura 1  —  T = 2π√m/k

Como as molas estão associadas em paralelo, a constante elástica da mola equivalente, que, substituindo as duas produz o mesmo efeito será k_e = k + k  —  k_e =2k e seu período será T’ = 2π√m/2k  —  T’ = 2π√m/k.1/√2.

T/T’ = √2  —  T’ = T/√2  — racionalizando  —  T’= T√2/2  Resposta C

 

2-

a) Como as duas molas de constantes k₂ estão em para, a mola equivalente terá constante k_e1 =30 + 30 = 60N/m. Então teremos:

                                                                      

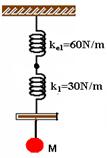
As duas molas acima estão em série, então a mola equivalente terá constante k_e, dada por: 1/k_e = 1/60 + 1/30  —  k_e = 20N/m,

que é a constante elástica total  equivalente do conjunto.

b) T = 2p√m/k  —  T = 2p√20/9 /20  —  T = 2.3.1/3  —  T=2s  —  f=1/T  —  f=0,5Hz

  

3-

As 3 molas de constantes k₂ estão em paralelo e serão substituídas por uma única mola de constante k_e1=3k₂.

As duas molas de constantes k₁ também estão em paralelo e serão substituídas por um única mola de constante k_e2=2k₁

Então, teremos:

                                                                     

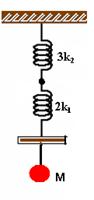
A mola resultante das duas acima, que estão em série, terá k_e, tal que: 1/k_e = 1/3k₂ + 1/2k₁  —  1/k_e = 2k₁ + 3k₂ / 6k₁.

K_e = 6k₁.k₂ / 2k₁ + 3k₂

O período desse sistema vale  —  T = 2pÖm/6k₁.k₂ / 2k₁ + 3k₂  —  T = 2pÖm(2k₁ + 3k₂)/6k₁.k₂

F = 1/T = 1/2p√6k₁.k₂ / m(2k₁ + 3k₂)

 

4-

a) A mola inteira (mola equivalente) tem constante elástica k’=10N/m sendo que 1/k’= 1/k + 1/k +1/k, onde k é a constante elástica de cada parte.

1/k’=3/k  —  1/12 = 3/k  —  k =36N/m

b) Paralelo  —  k­e=36 + 36 +36  —  k_e=108N/m  —  T=2π√m/k_e  —  T=2π√0,1/108  — T = 6.10^-2.π s

c) Série  —  k_e=12N/m  —  T=2π√m/k_e  —  T=2π√0,1/12  —  T= 18.10^-2.π s

 

5-

a) Peso de cada massa  —  P=mg  —  P=0,01.10  —  P=0,1N. Como as molas são ideais, suas massas são desprezíveis.

Observe que a mola 1 está sujeita à força F=0,3N (são as 3 massas que estão deformando-a)

F₁=k₁.x₁  —  0,3=0,1.x₁  —  x₁ = 3cm

A mola 2 está sujeita à F=0,2N (apenas duas massas estão deformando-a)

F₂=k₂.x₂  —  0,2=0,1.x₂  —  x₂= 2cm

Mola 3  —  F₃=k₃.x₃  —  0,1=0,1.x₃  —  x₃= 1cm

b) mola 1 – L₁= 23cm

    mola 2 – L₂= 22cm

    mola 3 – L₃= 21cm

c) 6 cm

Voltar para os exercícios