Impulso e Quantidade de Movimento – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Impulso e Quantidade de Movimento

01- A força que age sobre cada bola é a mesma (peso) e o impulso será maior para aquela que tiver maior tempo de contato com a mesa– R- B

02- R- A (veja teoria)

03- O impulso é numericamente igual à área do trapézio  —  I=(B + b).h/2=(25 + 10).30/2  —  I=525N.m  —  I=F.∆t  —  525=F.25  —  F=21N R- E

04- P=mg  —  360=m.10  —  m=36kg  —  Q=m.V=36.60/3,6  —  Q=600kgm/s R-C

05- t=0 – Q=12kgm/s  —  Q=mV_o  —  12=3.V_o  —  V_o=4m/s  —  E_co=m.V_o²/2=3.16/2  —  E_co=24J

t=6.10^-3s  – Q=0  —  Q=m.V  —  0=3V  —  V=0  —  E_c=mV²/2=3.0/2  —  E_c=0  —  ∆E_c=E_c – E_co=0 – 24  —  ∆E_c= -24J

06- Q=mV (função linear – 1^o grau)  —  E_c=mV²/2 (função quadrática – do 2^o grau)  R- C

07- Baixo – E_mb =mV²/2  —  topo – E_mt=mgh  —  mV²/2=mgh  —   V²/2=10.0,8  —  V=4m/s  —  Q=mV=60.4  Q=240=2,4.10²kg.m/s R- C

08- Supondo que, após o impulso contrário, ele continue se deslocando para a direita  —  I=Q – Q_o  —  40=mV – mV_o=2.15 – 2V_o  —  V_o=-5m/s (ele volta com velocidade de 5m/s  R- D

09-

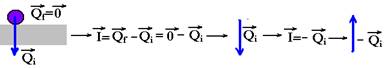
I= Q_i= Q_i= mV_i=0,01.3  —  I=3,0.10^-2N.s e para cima – veja figuras acima  R- A

10- a) 1⁰ trecho

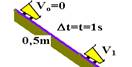
∆S=V_o.t + a.t²/2  —  0,5=0.1 + a.1²/2  —  a=1m/s²  —  V₁=V_o + a.t  —  V₁=0 + 1.1  —  V₁=1m/s

2^o trecho

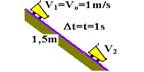
V₂=V_o + a.t  — V₂=1 + 1.1  —  V₂=2m/s

3⁰ trecho

 

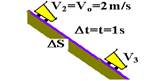
V₃=V_o + a.t=2 + 1.1  —  V₃=3m/s  —  Q₃=m.V₃=5.3  —  Q₃=15kgm/s

 

b) ∆S=V₀.t + a.t²/2=2.1 + 1.12  —  DS=2,5m

11- A energia mecânica da pedra na altura de 72m é só a energia potencial gravitacional – E_mi=mgh=10⁴.10.72  —  E_mi=72.10⁵J  —  como 90% foram dissipadas, sobraram  —  E_mf=10% de 72.10⁵=0,1.72.10⁵  —  E_mf=72.10⁴J que é o valor da energia cinética da pedra na parte inferior  —  72.10⁴=mV²/2  —  72.10⁴ = 10^4..V²/2  —  V=12m/s  —  Q=m.V=10⁴.12  —  Q=1,2.10⁵kg.m/s R- B

12- R –B (veja teoria

13- F.∆t=m∆V  —  F.0,01=0,12.(6)  —  F=0,72/0,01  —  F=72N  R- D

14- F.∆t=m∆V  —  F.10^-2=0,1.30  —  F=3.10²N   R- D

15- F.∆t=m∆V   —  F.∆t=m.V/2  —  F=mV/2∆t  R- D

16- F.∆t=m. ∆V  —  f­_m. 10^-3=m.4  —  f_m=4.10³m  —  P=mg=10m  —  f_m/P=4.10³m/10m  — f_m/P=400

17- E_c= m A energia mecânica da pedra na altura de 72m é só a energia potencial gravitacional – E_mi=mgh=10⁴.10.72  —  E_mi=72.10⁵J.

Como 90% foram dissipadas, sobraram  —  E_mf=10% de 72.10⁵=0,1.72.10⁵  —  E_mf=72.10⁴J que é o valor da energia cinética da pedra na parte inferior  —  72.10⁴=mV²/2  —  72.10⁴ = 10^4..V²/2  —  V=12m/s  —  Q=m.V=10⁴.12  — Q=1,2.10⁵kg.m/s R- B

E_c=mV_i²/2  —  4π²=2Vi² /2  —  V=2πm/s  —  I=mV – mV_o  —  I=2.2π – 0  —  I=4πN.s

18- Velocidade com que ele chega à cama a partir de uma altura de 3,2m  —  mgh=mV₁²/2  —  10.3,2=V₁²/2  —  V₁=8m/s  — 

Velocidade com que ele sai da cama atingindo h=2,45m  —  mV₂²/2=mgh  —  V₂²/2=10.2,45  —  V₂=7m/s

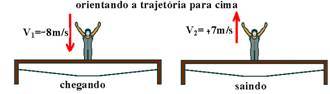
F.∆t=m(V₂ – V₁)  —  F.0,4=80(7 – (-8))   —  F= 1.200/0,4  —  F=3,0.10³N

19-Veja o esquema abaixo:

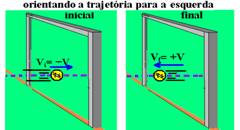
I = m.V_f – m.V_i  —  I = m.(+V) – m.(-V)  —  I = 0,3.5 – (- 0,3.5)  —  I= 1,5 + 1,5—  I=3,0kg.m/s  R- C

20- Pássaro- antes V_i=0 e depois ele adquire a mesma velocidade que o avião V_f=900/3,6=250m/s  —  F.∆t=m(V_f – V_i)  — F.0,001=2.(250 – 0)  —  F=500/0,001  — F=500.000N ou F=5,0.10⁵N

21– a)Queda livre de uma altura de 80m  —  V²=V_o² + 2.g.h  —  V²= 0² + 2.10.80  —  V=40m/s  —  ∆V=40m/s  —  F.∆t=m.∆V  —  F.0,05=50.40  —  F=40.000N

b) a=∆V/∆t=40/0,05  —  a=800m/s²   —  a_l=8.10  —  a_l=80m/s²  —  a/a_l=800/80  —  a/a_l=10   

22- Observe a figura abaixo:

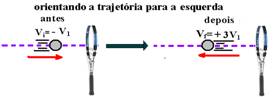
P=mg=10m  —  F=60.p=60.10m  —  F=600m  —  F.Dt=m(V_f – V_i)  —  600m.0,2=m(+3V₁) – (-V₁)  —  120=3V₁ + V₁  —  V₁=120/4  —  V₁=30m/s  R- C

23- R- B (veja teoria)

24- a) Veja pela expressão F.∆t=m.∆V, que m e ∆V são constantes (mesma xícara e mesma variação de velocidade) e assim, teremos:

F.∆t=constante, portanto se você aumentar o intervalo de tempo do choque, estará diminuindo a intensidade da força máxima que a xícara troca com o tapete. t

b) F.∆t=m.∆V  —  F.0,5=0,1.2  —  F=0,2/0,5  —  F=0,4N  —  F.0,01=0,1.2  —  F=0,2/0,01  —  F=20,0N

25-1- Verdadeira – quando ele deixa o degrau, está em queda livre e, nesse caso, a força resultante sobre ele é seu peso e a variação do seu momento linear (quantidade de movimento) é I=P.∆t=m∆V=∆Q.

2 -Verdadeira – cálculo da velocidade com que ele chega ao solo – queda livre com Vo=0 – Torricelli – V²=Vo² + 2.g.∆S  — V²=0² + 2.10.0,5  —  V=√10m/s – velocidade com que chega ao solo  —  durante o choque com o solo sua velocidade varia de √10m/s a zero e o módulo dessa variação é∆V=√10m/s enquanto que sua altura diminui de ∆S=3cm=0,03m , numa desaceleração a de  —  V²=Vo² +2.(-a).∆S  —  0²=(10)² -2.a 0,03  —  a=500/3m/s²  —  força que ele troca com o solo e que produz essa desaceleração  —  F=m.a=70.500/3  —  F»11.667N  —  peso correspondente à massa de 1ton=1.000kg – P=1.000X10 – P=10.000N  —  portanto – F>P

3- Verdadeira – é a força de contato, que os pés trocam com o solo.

4- Verdadeira – (veja teoria)

26- Dados: v_o = 0  —  v = 162 km/h = 45 m/s  —   m = 170 g = 0,17 g  — Δt = 10^-2 s  —  considerando que força aplicada pelo stick é a resultante, pelo teorema do impulso, vem:

I = ΔQ  —  F.Δt = m.(v – v_o)  —  F.(10^-2) = 0,17.(45)  —  F = 7,65×10² N  —  R- B 

27- Dados  —   m = 0,8 kg  — v_o = 93,6 km/h = 26 m/s  —   v = 280,8 km/h = 78 m/s  —  o enunciado afirma que antes da colisão a velocidade relativa entre a mola e o capacete é V_R=78 – 26=52m/s, e no instante após a colisão a velocidade relativa é nula  —  assim, a quantidade de movimento da mola após a colisão em relação ao capacete é nula  —  I=ΔQ  —  F.Δt=mΔV  —  F.Δt=m.(V – V_o)  —  F.0,026=0,8.(52 – 0)  —  F=1.600N

R- B

28- Observe na figura abaixo as forças que atuam sobre a polia  —  o dinamômetro indica a intensidade da força de tração no fio

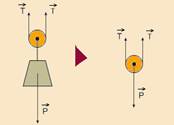
 ao qual está ligado  — T = 60 N  —  como o corpo C está em equilíbrio  —  2T = P  —   2(60) = m(10)  —   m = 12 kg  —  depois que o fio é cortado o corpo de massa 12kg cai em queda livre com aceleração a=g=10m/s² e, após 1s terá velocidade  —  V=V_o + gt  —  V=0 + 10.1  —  V=10m/s  —  nesse instante terá quantidade de movimento   —  Q=mV=12×10  —  Q=120kg.m/s  —  R- D

29- Em todo gráfico F x t, o impulso é numericamente igual a área compreendida entre a reta representativa e o eixo t, no caso a

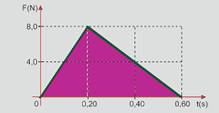
área do triângulo  —  I=b.h/2=0,6.8/2  —  I=2,4N.s  —  pelo Teorema do Impulso  —   o impulso da força resultante é igual à variação da quantidade de movimento (ΔQ)  —  I = ΔQ = m Δv  —  2,4 = 0,1 (v – 0)  —   v = 24 m/s  —  R- C

30- Observe pelo gráfico que, quando V=1m/s, E_c=1J  —  substituindo na equação E_c=mV²/2  —  1=m.1²/2  —  m=2kg  — quandoV=5m/s, a quantidade de movimento Q será  —  Q=mV=2.5  — Q=10kg.m/s

31- Considerando essa força como a resultante  —  I = ΔQ  —  como há apenas mudança de sentido e não de direção (movimento retilíneo), o impulso pode ser obtido pela área entre a linha do gráfico e o eixo t, como indicado na figura  —  como a força F tem

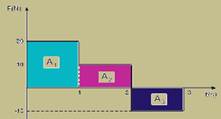
módulo constante em cada intervalo de tempo, o impulso também pode ser obtido pela expressão  —  I_F = F.Δt  — │I_FR│=│ΔQ│=m│V – V_o│ —  A₁ + A₂ – A₃=m(V – V_o)  —  1×20 + 1×10 – 1×10=10(V – 0)  —  10V=20  —  V=2m/s

32- Justificando as falsas:

01) Considerando que a força F à que se refere a afirmativa seja a força resultante e que ela seja constante, temos, pelo teorema do impulso  — I=ΔQ = FΔt  —  F=ΔQ/Δt  —  nesta expressão, observe que o coeficiente angular dessa função é F.

02) A quantidade de movimento no instante t = 0 é Q_o = m v_o  —  a quantidade de movimento somente será nula se a velocidade inicial for nula.   

R- (04 + 08 + 16)=28

33- Observe as figuras abaixo:

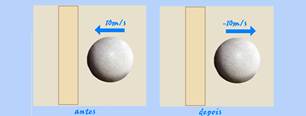
Teorema do impulso  —  I=ΔQ  —  F.Δt=mΔV  —  F.0,04=0,75{10 – (-10)}  —  F=1,5/0,004  —  F=375N  —  R- B

34- 01. Correta  —  veja teoria

02- Falsa  —  não é a variação da quantidade de movimento que tem sempre a direção e o sentido da velocidade mas sim, a quantidade de movimento.

04. Correta  —  veja teoria

08. Falsa  —  veja teoria

16- Falsa  —  veja teoria

R- (01 + 04)=05

 

35- Cálculo da aceleração do atleta  —  quando t=2s, V=2,2m/s  —  V=Vo + a.t  —  2,2=0 + a.2  —  a=1,1m/s2  —  força resultante sobre o atleta  —  F=m.a=85.1,1  —  F=93,5N  —  impulso sobre o atleta nesses 2s  —  I=F.∆t=93,5.2  —  I=187N  —  R- D

 

36- Leopardo  —  Ql=ml.vl=120.60=Q1=7.200kg.m/s  —  automóvel  —  Qa=ma.va=1.100×70=Q2=77.000kg.m/s  —  caminhão  —  Qc=mc.vc=Q3=3.600×20=72.000kg.m/s  —  cofre  —  velocidade com que ele chega ao solo  —  V2 = Vo2 + 2.g.h = 0 + 2.10.5  —  V=10ms  —  Qco=mco.Vco=300.10  —  Qco=Q4=3.000kg.m/s  —  R- C

37- Q=m.V=6.10-2.60  —  Q=3,6kg.m/s  —  Ec=m.V2/2=6.10-2.(60)2/2  —  Ec=108J

38- Um  ônibus   que  trafegava  inicialmente  a  54 km/h foi freado bruscamente, como forma de impedir um impacto iminente com o veículo

à sua frente. Um passageiro de massa igual a 60 kg, surpreendido pela manobra violenta, foi arr

– I. Correta  —  F=ma  —  a=∆V/∆t  —  F=m∆V/∆t  —  F.∆t = m. ∆V  —  F.0,3 = 60.15  —  F=900/0,3  —  F=3.000N.

II. Correta  —  ∆E_c=mV²/2 – m.V_o²/2=60.0²/2 – 60.15²/2=0 – 13.500/2  —  ∆E_c= – 6.750J.

III. Falsa  —  P_o=W/∆W/∆t=∆E_c/∆t  —  P_o=6.750/0,3  —  P_o=22.500W=22,5kW.

IV. Falsa  —  ∆Q=m. ∆V=60.(0 – 15)= – 900kg.m/s.

R- A

 

Voltar para os exercícios