Forças no Movimento Circular

Resolução comentada dos exercícios de vestibulares sobre

Forças no Movimento Circular

 01– F_C=m.W².R  —  F_C=1.000.(10)².20  —  F_C=2.10⁶N  R- A

02– A força de atrito estático será máxima quando o carro estiver na iminência  de escorregar para fora da pista e nesse caso F_atemáximo=μ_eN=m_eP=μ_emg  —  F_c=F_atmáx  —  mV²/R=μ_emg  —  , que é a máxima velocidade com que ele consegue fazer a curva sem derrapar  —  V=√m.R.g  —  (15)²=(√m.50.10)²  —  225=500m  —  m=0,45  R-C

03– R- E (vide teoria)

04– A velocidade mínima para que o carvão não caia ocorrerá quando a força de compressão no ponto superior for nula, ou seja, quando N=0  —  F_C=P + N  —  F_C=P + 0  —  F_C=P  —  m.V²/R=m.g   —  V=√(R.g)  —  V=√0,8.10  —  V=√8=2√2m/s  R- C

05– R-A (vide teoria)

06– a_C=V²/R  —  a_C=9/2  —  a_C=4,5m/s²  R- D

07– Como a curva é horizontal, a força resultante centrípeta que é radial e dirigida para o centro da circunferência deverá ser também horizontal. R- A

08– Colocando as forças:

a é o ângulo de inclinação das asas em relação ao plano horizontal  —   é a força de sustentação aplicada pelo ar e que é perpendicular às asas  —   é o peso.

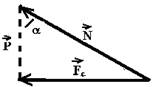
tga=cateto oposto/cateto adjacente  —  tga=F_c/P  —  tgaα=(m.V²/R)/mg 

   —   substituindo os valores  —  100=√(R.9,5.√3)  —  10.000=R.9,5.1,7  —  R=10.000/16,15  —  R=619,2m  R- A

09– Colocando as forças:

 

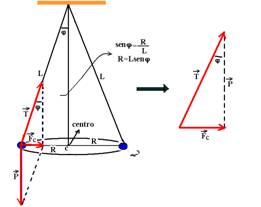
a) P=m.g  —  P=0,5.10  —  P=5N  —  Da figura da direita  —   cosφ=P/T  —  0,5=5/T  —  T=10N

b) Da figura da direita – tgj=F_c/P  —  tgφ=(mV²/R)/mg  —  tgφ=V²/Rg   —  R=Lsenφ  —  tgφ=V²/L.senφ.g  — em função da velocidade angular W=V/R  —  V=W.R  —  senφ/cosφ=W².R²/R.g  —  senφ/cosφ=W².R/.g  —  senφ/cosφ=W².Lsenφ/.g  — 

     —   substituindo os valores  —  W=√(10/1,25.0,5)  —  W=√16  —  W=4rad/s

10– Sendo o movimento circular a força resultante sobre a mosca é a centrípeta de direção radial, sentido para o centro da circunferência e intensidade Fc₌m_.V²/R. Como m e V são constantes,F_c e R são inversamente proporcionais, ou seja, quanto menor é o raio R, maior será a intensidade da força resultante centrípeta F_c. R- D 

11– Colocando as forças:

 

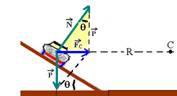
No triângulo hachurado  —  tgθ=cateto oposto/cateto adjacente  —  tgθ=F_C/P  —  tgθ=(mV²/R)/mg  —  V²=R.g.tgθ V=√R.g.tgθ  —  máxima velocidade que o carro deve ter para efetuar a curva sem atrito  —  V=√200.10.0,2  — V=20m/s que dividido por 3,6 nos fornece V=72km/h  R- B

12– A máxima velocidade com que o carro consegue realizar a curva sem perder contato com o solo ocorre quando a força de

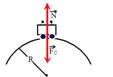
compressão  entre os pneus do carro e o solo é nula, ou seja, N=0  —  F_C=P-N  —  mV²/R=mg – 0  —  V²/R=g  —  V=√R.g   —  10=√R.10  —  (10)²=(√R.10)²  —  100=10R    —  R=10m  R- C

13– a força resultante centrípeta  , que é dirigida sempre para o centro da circunferência, no caso, para

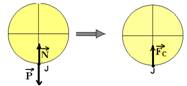
cima, é a diferença vetorial entre  e  , de intensidade  —  F_C=N – P  —   m.V²/R= N – m.g  —  N=m.g + mV²/R

N=50.10 + 50.100/2  —  N=3.10³N

14– Ponto A – lombada

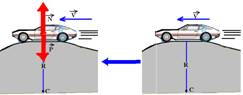
A força resultante centrípeta que é sempre dirigida para o centro da circunferência que é para baixo, ou seja, FC=mV²/R    — 

P – N=mV²/R   —   mg – N = mV²/R  —   N=2.10³.10 – 2.10³.100/100  —  N= 20.10³ – 2.10³  —  N=18.10³N   

Ponto B – depressão

 

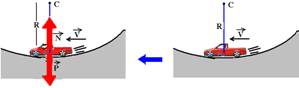
A força resultante centrípeta que é sempre dirigida para o centro da circunferência que é para cima, ou seja, F_C=mV²/R    — 

N – P=mV²/R  —  N=20.10² + 2.10³  —  N=22.10³N

Ponto C – horizontal  —  N=P  —  N=20.10³N

Observe que N_B>N_C>N_A

15–

01- Falsa – em qualquer movimento circular, uniforme ou não, existe sempre uma força resultante centrípeta.

02- Correta – vide 01

04- Correta, a força resultante centrípeta tem sempre direção radial e sentido para o centro da trajetória.

08-  Correta. Observe nas figuras abaixo que =.

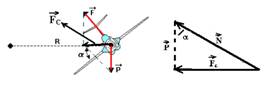
Tg45^o=F_C/P  —  1=F_C/10.000X10   —   F_C=100.000N

16- F_C=m.V²/R  —  100.000=10.000.V²/1.000  —  V=Ö10⁴  —  V=100X3,6=360km/h.

R: 02 + 04 + 08 + 16=30

16– Para que o astronauta permaneça na mesma posição “colado” à nave, ele deve ter a mesma velocidade angular W que ela e também o mesmo período T (tempo que ela demora para efetuar uma volta completa), que é de 20s.

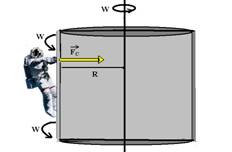
T=20s  —  W=2π/T  —  W=2π/20=p/10  —  W=π/10rad/s  —  F_C=m.W².R  —  F_C=70.(π²/100).10  —  F_C=7π²N

17– a) O “peso” do astronauta é percebido pela reação normal  das paredes da nave sobre ele, que é a própria força resultante centrípeta de intensidade N=mV²/R ou N=m.W².R, que nesse caso é seu próprio peso, ou seja, N=P=m.g.

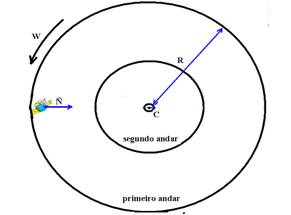
Primeiro andar – raio R  —  m.g=m.W².R  —  W=√(g/R)

b) ) O “peso” do astronauta é percebido pela reação normal  das paredes da nave sobre ele  —  N=F_C=m.W².(R-h)  — 

 

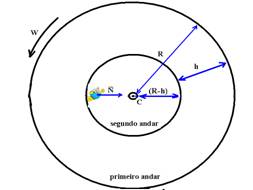
N=m.(√g/R)².(R-h)  —  N=m.g.(R-h)/R  —  Observe na expressão N=m.W².R que se a nave girar com W constante (que é a mesma para todos os andares) e como a massa do astronauta é a mesma, a “gravidade” N é diretamente proporcional ao raio R. Assim, a medida que o astronauta se aproxima do centro C de rotação do sistema a “gravidade” vai diminuindo até se anular no centro C, onde o astronauta tem sensação de ausência de peso (imponderabilidade).

18– a) A velocidade vetorial tem sempre o sentido do movimento e é sempre tangente à trajetória em cada ponto.

 

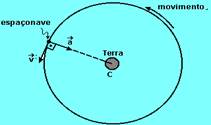
b) Do enunciado F_C=1,5GMm/R², mas sua intensidade também é F_C=mV²/R  —  m.V²/R=1,5.G.M.m/R²  —  V=√(1,5.G.M)/R

19– a) Como o ponto de entrada do freguês coincide com o ponto de saída, o tempo mínimo de permanência ocorre quando o restaurante efetua um volta completa, o que ocorre no período T  —  W=2π/T   —   p/1800=2π/T  —  T=3.600s ou T=1h

b) F_C=m.W².R=50.( p/1800)².20  —  F_C=50.(3,14)².20/11(1.800)²  —  F_C=3.10^-3N

20– a)

b) Somando vetorialmente com  obtemos a força resultante centrípeta , conforme a figura abaixo.

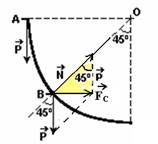
Do triângulo hachurado  —  tg45^o=F_C/P  —  1=(m.V²/R)/m.g  —  V²=R.g  —  sen45^o=F_C/N  —  √2/2=(m.V²/R)/N  —  √2/2=m.V²/R.N   —  √2/2=m.R.g./R.N  —  N=√2.m.g

21– a) Tração e peso. A tração sobre o fio no sentido do ponto fixo, enquanto que o peso é vertical para baixo, conforme a figura abaixo.

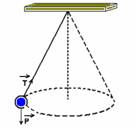
A soma vetorial da força de tração no fio e a força peso nos fornece a força resultante centrípeta.

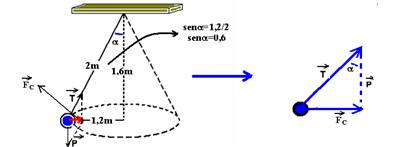
No triângulo da direita  —  tga=F_C/P=m.V²/m.R.g  —  1,2/1,6=V²/1,2.10  —  V=√9  — V=3m/s

senα=F_C/P  —  0,6=(m.V²/R)/T  —  0,6= m.V²/R.T  —  0,6=0,4.9/1,2.T  —  0,72T=3,6  —  T=5N

22– O período corresponde ao tempo que ele demora para efetuar uma volta completa  —  regra de três  —

60 voltas – 30s

1 volta   –   T

60T=30  —  T=1/2s  —  W=2π/T  —  W=(2π)/1/2  —  W=4πrad/s  —  Como não há movimento vertical, peso e normal se anulam e, na horizontal a tração no fio é a própria forca resultante centrípeta  —  F_C­=T=m.W².R=0,5.(4π)².1  —  T=0,5.16.10.1  — T=80N  R- B

23– a) 2,0^.10⁴.                    b) 2,6^.10⁴.                      c) 3,0^.10⁴.                     d)2,0^.10³.                     e) 3,0^.10³.

Como ele está em movimento circular existe uma força resultante centrípeta que é sempre dirigida para o centro da circunferência que é para cima, ou seja, F_C=mV²/R  ou  F_C=mW².R  —  N – P=mV²/R  ou N – P=mW²R.

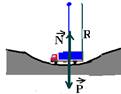
N – 2.10³.10=2.10³.(30)²/3.10²  —  N=2,6.10⁴N

24– R- B (vide exercício 13)

25– Como o movimento é circular e uniforme, a força centrípeta = e a aceleração centrípeta =  tem a mesma direção

(radial) e o mesmo sentido (para o centro da circunferência) e ambas são sempre perpendiculares ao vetor velocidade , que é sempre tangente à trajetória em cada ponto e tem o sentido do movimento. R- D

26– Nesse caso, a força centrípeta é o F_at que evita com que ele escorregue e saia pela tangente. A força de atrito estático será máxima quando o carro estiver na iminência  de escorregar para fora da pista e nesse caso F_atemáximo=μ_eN=m_eP=μ_emg  —  F_c=F_atmáx  —  mV²/R=μ_emg  —  , que é a máxima velocidade com que ele consegue fazer a curva sem derrapar e,

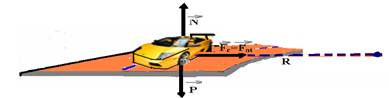
nesse caso, o coeficiente de atrito deve ser mínimo  —  20=√μ_e.100.10  —  400=1.000.μ_e  — μ_e=0,4  R- E 

27– Colocando as forças:

 

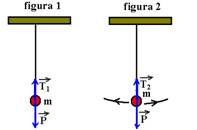
figura 1 – repouso – F_R=0  —  T₁=P    —    figura 2 – F_C=T₂ – P  —  T₂ – P = m.V²/R  —  T₂=P + m.V²/R  —  T₂>T₁

28– A velocidade mínima para que o sistema não caia ocorrerá quando a compressão no ponto A for nula, ou seja, quando N=0  —  F_C=P + N  —  F_C=P + 0  —  F_C=P  —  m.V²/R=m.g  —  V=√R.g  —  velocidade mínima do sistema (moto + motociclista) no ponto mais alto para fazer a curva e não perder contato com a superfície interna do globo, ou seja, não cair.

V=√4,9.10  —  V=7m/s  R- C

29– No ponto mais alto do morro as forças que agem sobre os dois carros são o peso  e a força de contato com o solo .

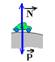
Na iminência de perder contato com o solo, N=0  —  F_C=P – N  —  P – N=m.V²/R  —  P – 0=m.V²/R  —  mg=mV²/R  — V=√R.g  —  verifique pela fórmula que essa velocidade não depende da massa  —  R- D

30– R- C (veja exercício 27)

31- a e b) Observe a figura abaixo  —  T – intensidade da força de tração no fio  —  P – intensidade do peso do acrobata  —  F_C

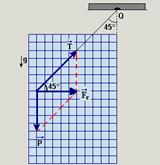
  – intensidade da força resultante centrípeta  —  sen45^o=P/T  —  Tsen45^o=P  —  T.√2/2=mg  —  cos45^o=F_c/T  —  F_c=Tcos45^o  — mV²/R=T.√2/2  —  mg=mV²/R   —  V²/R=g  —  V=√Rg=√4,9.10  —  V=7m/s  —  uma volta completa com velocidade de 7m/s  —  V=ΔS/T  —  7=2πR/T  —  7=2.3,14.4,9/T  —  T≈4,4s

c) Sabemos que T.cos45° = m.g  —  T.√2/2 = 60.10  —  T.0,71 = 600  —   T ≈845 N

Nas condições do teste de segurança  —  3.T = M_o.g  —  M_o = 3.845/10  —  M_o ≈253,5 kg 

32-  Observe a a figura da direita abaixo  —  R=4 + 10senθ=4 + 10.1/2  —  R=9m

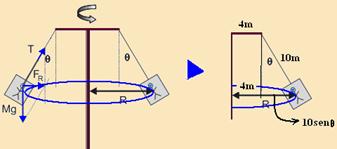
 Observe a figura da esquerda acima  —  na vertical  —  Tcosθ=Mg  —  Tcos30^o=1000.10  —  T=10.000/0.87  —  T=11.494N

A força resultante centrípeta F_R, horizontal, é a componente Tsen30^o  —  F_R=F_c=Tsen30^o=11.494.1/2  —  F_c=5.747N 
33- O chamado estado de imponderabilidade ocorre exatamente porque todos os corpos dentro da estação espacial e a própria estação espacial estão sujeitos a mesma aceleração  —  o que valida a alternativa A  —  como existe aceleração (gravitacional) da Terra sobre a estação e tudo mais que ela contém, o astronauta possui peso, o que invalida a alternativa B  —  alternativa c, absurda  —   o estado do astronauta, bem como de tudo mais da estação não é inercial, pois, como já dito, existe aceleração sobre os corpos em órbita  —  a velocidade do astronauta pode até ser momentaneamente maior ou menor que a velocidade da própria estação, se ele se desloca dentro dela. Como ele flutua, no mesmo local da estação, subentende-se que a velocidade dele é a da estação, o que invalida a alternativa E.

R- A 

34- O objeto solto bem como o próprio satélite está sujeito à força gravitacional terrestre e logo ambos têm peso  —  admitindo que o movimento do satélite e do corpo são circulares e uniformes, a aceleração centrípeta será a aceleração gravitacional  —  a alternativa c é falsa, pois se uma pessoa estiver solta dentro da nave ela não experimenta sensação de peso.

R- B 

35- Conforme o diagrama anexo, as forças que agem no carro são o peso  e a normal . Como o movimento é circular e uniforme, a resultante dessas forças é centrípeta (radial), .

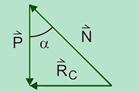
tga = R_c/P=ma_c/mg  —  a_c=gtgα  —  como a e g são constantes, a aceleração centrípeta (radial, dirigida para o centro) tem módulo constante. 

R- D

36- As forças que atuam sobre o (automóvel + motorista) estão indicadas na figura  —  a força resultante centrípeta é vertical e para

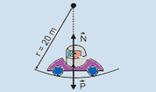
cima, pois é dirigida para o centro da circunferência  e tem intensidade F_c=mV²/R  —  N – P=mV²/R  —  N=860.10 + 860.(20)²/20  —  N=25.800N  —  R- D

37- O enunciado sugere tratar-se de um pêndulo cônico ou pêndulo composto  —  as figuras abaixo ilustram a situação descrita  — 

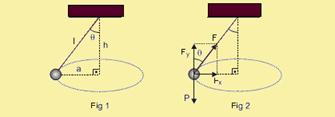
Na Fig 1  —  h²  +  a²  = l²  —  h² = l² – a²  —  h = (I)  —  senθ=a/l  —  cosθ=h/l  —  na Fig 2  —  a componente horizontal da tração (F_x) é a resultante centrípeta (F_c)  —  F_x = F_c  —  F sen q = mV²/a  —  F.(a/l)=mV²/a  —   F =mV²l/a²(II)  —  como o movimento se dá num plano horizontal, a resultante das forças verticais é nula  —  assim, a componente vertical da tração (F_y) equilibra o peso da esfera pendular (P)  —  F_y = P  —   F cos q = m g  —  F.(h/l) = m g  —  F = mgl/h(III)  —  igualando (II) e (III)  —  mV²l/a²=mgl/h  —  V²=a²g/h (IV)  —  operíodo (T) é o intervalo de tempo gasto em cada volta (DS = 2pR=2πa)  —   

v = ΔS/Δt=2πa /T (V)  —  substituindo (V) em (IV)  —  (2πa/T)²=a²g/h  —  4π²a²/T²=a²g/h  —  T²=4π²h/g  —  T=2π√h/g (VI)  –

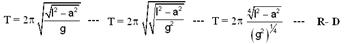
38- Observe a figura abaixo que mostra as forças que agem sobre a pessoa: 

 

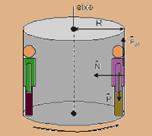
01) Correta  —   força normal  é sempre perpendicular a superfície de apoio, conforme ilustra a figura acima. Nesse caso ela é dirigida para o centro, portanto é uma força centrípeta.
02) Falsa  —  como a pessoa efetua movimento circular uniforme, na direção horizontal a normal age como resultante centrípeta  e, na direção vertical, a força de atrito  deve equilibrar o peso. O piso somente deve ser retirado quando a força de atrito estática máxima for maior ou igual ao peso, caso contrário a pessoa escorrega pelas paredes  —  N=mV²/R  —  F_at ³ P  —  m N ³ m g  —  inserindo nessa expressão a expressão anterior  —  μmV²/Rmg  —  μRg/V²  —  V√(Rg)/μ  —  nessa expressão, vemos que a massa da pessoa não interfere e que a velocidade mínima com que o piso pode ser  retirado depende apenas do raio do rotor da intensidade do campo gravitacional local e do coeficiente de atrito entre as roupas da pessoa e a parede do rotor.

04) Verdadeira  —  conforme demonstração no item anterior.

08) Falsa  —  o coeficiente de atrito depende apenas das características das superfícies em contato.

16) Falsa  —  conforme justificativa do item anterior.

R-(01 + 04) = 05

39- Dados  —   v = 216 km/h = 60 m/s  —   m = 6 kg  —   r = 72 m  —  a força que o piloto deve exercer sobre o conjunto cabeça-capacete é a resultante centrípeta  —  F_c=mV²/R=6.(60)²/72  —  F_c=300N  —  para que um corpo tenha esse mesmo peso, quando sujeito à gravidade terrestre, sua massa deve ser  —  P/g=300/10  —  m=30kg  —  R- B

40-  Dados  —  h = 2 m  —   g = 9,8 m/s²  —   D_ac = 1% g = g/100=0,098 m/s²  —  um habitante no interior da nave gira com a mesma velocidade angular (w) que ela  —    diferença entre as acelerações centrípetas nos pés  e na cabeça deve ser igual a 1% da aceleração da gravidade na Terra.

Pés  —  = g  —  cabeça  —    —  =g/10  —  =g/10  —  =g/10  —    —  w² = 0,049  —  w²r = g  —  0,049 r = 9,8  —   r = 9,8/0.049  —  r=200m

41- Dados  —  v_o = 0  —   m = 1.000 kg  —   H = 30 m  —   d = 20 m  —  r = 10 m  —  observe a figura abaixo  —  cálculo da

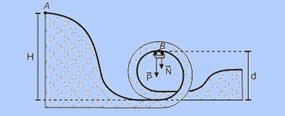
 velocidade no ponto B pela conservação de energia mecânica  —    —  mgH=mgd + mV²/2  —  V²=2h(H – d)  — 

V²=20.(30 – 20)  —  V²=200  —  no ponto B, a resultante das forças que agem sobre o carro são radiais, portanto a aceleração é centrípeta  —  a=a_c=V²/R=200/10  — a=20m/s²  —  no ponto B, a resultante é centrípeta e a força vertical que o trilho exerce no carro é a normal   —  no ponto B a força resultante centrípeta tem direção vertical e sentido para baixo (centro da circunferência)  —  F_c=N + P=ma  —  N=ma – mg  —  N=1.000(20 – 10)  —  N=10.000N

42- No ponto mais alto quando N=0  —  F_c=mV²/R  —  N + P=mV²/R  —  0 + mg=mV²/R  —  V=√rg  —  a_c=V²/r=rg/r  —  a_c=g  —  R- E

43- 01. Falsa  —  a intensidade da força de tensão em C é maior que o peso  —  existe uma resultante centrípeta vertical e para cima.

02- Correta  —  veja teoria

04- Falsa  —  veja 08

08- a menor velocidade e a menor energia cinética ocorre quando a tensão T é nula  —  T + P=mV²/R  —  mg=mV²/R  —  V=√Rg  —  V=√1.10  —  V=√10m/s  —  E_c=mV²/2=0,5.10/2  —  E_c=2,5J

16- Falsa  —  T + mg=mV²/R  —  T=0,5.10 + 0,5.900/2  —  T=225N

32- Falsa  —  F_R=F_c=mV²/R=0,5.900/1  —  F_R=450N

R- (2 + 8)=10

44- A aceleração centrípeta é dada pela expressão a_cp = v²/R. Substituindo os valores para a velocidade de módulo constante do carro, v = 10 km/h, e para o raio da circunferência, R = 5 m = 0,005 km, obtém-se que a_cp = 20.000 km/h².

R- E

45- W=4.360/2  —  W=720 ^o/s  —  R- B

46-

Leia atentamente as informações a seguir:

Carro em pista sobrelevada de ângulo θ com a horizontal, sem atrito em pista circular de raio R, contida num plano horizontal.

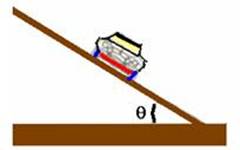
As duas forças que agem sobre o carro, independente do atrito são seu peso  e a reação do solo . Para que o carro complete a curva a força resultante centrípeta   deve ser a soma vetorial de  com  e deve ser radial e dirigida para o centro C  da pista circular de raio R (veja figura abaixo).

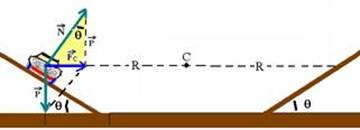
No triângulo hachurado  —  tgθ=cateto oposto/cateto adjacente  —  tgθ=F_c/P  —  tgθ=(mV²/R)/mg  —  V²=R.g.tgθ

velocidade que o carro deve ter para efetuar a curva sem atrito (ou que seus pneus percam contato (atrito) com a pista).

V=√(R.g.tgθ)  —  V²=R.g.tg30^o  —  100²=R.10.0,58  —  R=10000/5,8  —  R=1724,14m  —  R- D.

47-

a) Correta  —  a_c=V²/R  —  observe que a aceleração centrípeta é inversamente proporcional ao raio da pista  —  menor raio, maior aceleração centrípeta.

b) Falsa  —  W=V/R  —  a velocidade angular depende do raio da pista.

c) Falsa  —  A só poderia acompanhar B se eles tivessem a mesma velocidade angular (W=∆θ/∆t), ou seja, eles devem “varrer” o mesmo ângulo no mesmo tempo.

d) e e) Falsas  —  analise a expressão da força centrípeta  —  F_c=m.V²/R.

R- A

48-

Em todo movimento circular existe sempre uma força resultante com direção radial e sentido dirigido para o centro da circunferência, de intensidade Fc=mV2/R, denominada força resultante centrípeta  —  R- C

 

Voltar para os exercícios