Lei de Hooke e Associação de molas – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Lei de Hooke e Associação de molas

 01– A mola fica deformada de x=(22 – 10)=12cm  —  x=12cm 

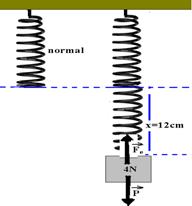
Numa deformação de 12cm  —  F_e = P = 4N  —  F_e = K.x  —  4 =K.12  —  K=1/3 N/cm

K é constante para qualquer deformação (lei de Hooke)  —  para F_e=P=6N  —  F_e=K.x  —  6=1/3.x  —  x=18cm  —  fica deformada de 18cm e seu comprimento será L=18 + 10 = 28cm

02– R- D – vide teoria

03– K=300N/m e é constante (obedece à lei de Hooke). A máxima deformação da tira de borracha é de 28cm (Dx=28cm=0,28m)  — 

F=K.Dx  —  F=300.0,28  —  F=84N  R-E

04– a) As forças que atuam sobre a caixa são o peso,  vertical e para baixo, a força normal, exercida pelo plano e perpendicular a ele, e a força elástica, exercida pela mola.

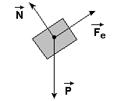
b) Como a caixa está em repouso, temos: F_R=0  —  P_P = F_e

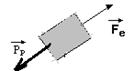
m.g.sen30^o = K.x  —  5.10.1/2 = 100.x  —  x=25/100  —  x=0,25m

05- Em 2  —  F=Kx  —  10=K.5  —  K=2N/cm  —  em 3  —  F=Kx  —  25=K.12,5  —  K=2N/cm  —  Sim, obedece, pois K é constante

06- Após o sistema entrar em movimento com aceleração , as molas já se encontram deformadas de x_A e x_B e a mola A sujeita à força de tração   —  

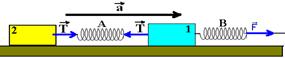
   bloco 2   —  F_R=m₂.a  —  T=8a I  —  bloco 1  —  F_R=m₁a  —  F – T =12a  II  —  resolvendo I com II  —   F=20a e T=8a   —  sendo as molas idênticas, elas possuem a mesma constante elástica K  — F=Kx_B  —  x_B=20a/K  —  T=Kx_A  —  8a = Kx_A  — 

x_A=8a/K  —  x_A/x_B=8a/K/K/20a  —  x_A/x_B=2/5 

07- a) balde e elevador em repouso  —  F_R=0  —  P=F_e  —  mg=Kx_o  —  x_o=mg/K

b) balde e elevador subindo com aceleração a  —  F_R=ma  — F_e – P=ma  —  K.(x_o + d) – mg=ma  —  a=(K.(x_o + d) – mg)/m

08- Quando o fio é cortado, a esfera desce 1m e pára momentaneamente e, nesse instante temos o esquema abaixo:

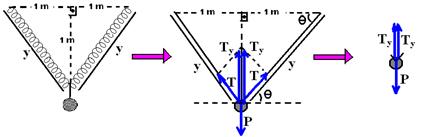
T – força de tração em cada uma das molas e o peso da esfera – P=mg=5,1.10  —  P=51N  — aplicando Pitágoras num dos triângulos retângulos  —  y²=1²+ 1²  —  y=√2=1,41m  —  observe que y é o comprimento da mola na posição normal (1m) e que Δx é sua deformação e que y=1 + Δx  —  1,41=1 + Δx  —  Δx=0,41m  —  observe também que senӨ=1/y=1/√2  —  senӨ=√2/2=1,41/2  —  senӨ=0,7  —  T_y=TsenӨ=0,7T  —  como a esfera está em equilíbrio, P=2T_y  —  51=2.0,7T  —  T≈36N  —  T=F_e=K.Δx  —  36=K.0,41  —  K=87,8N/m

09- a) F_e=Kx  —  0,40.10^-6=K.0,40.10^-6  —  K=1,0N/m

b) F_e=ma  —  a=25.10=250m/s²  —  Kx=m.250  —  1.0,5.10^-6=m.250  —  m=5.10^-7/250=0,02.10^-7  —  m=9,0.10‑9‑kg

10- Deformação da teia quando em equilíbrio Δx=0,01L  —  Δx=10^-2L  —  no equilíbrio P=F_e  —  mg=KΔx  —  70.10=10¹⁰.A/L.10^-2L  —  A=10^-6m²

11– Depois das oscilações iniciais terem sido amortecidas, as molas não se deformam mais e o conjunto se desloca coma aceleração constante a;

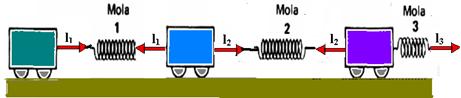
Bloco 3  —  l₃ – l₂=ma I  —   bloco 2  —  l₂ – l₁=ma II   —   bloco 1  —  l₁=ma III  —  III em II  —  l₂ – ma = ma  —  l₂=2ma  

Somando I, com II com III  —  I₃=3ma       R- C

 

Associação de molas

12– Período T da mola da figura 1  —  T = 2p√m/k

Como as molas estão associadas em paralelo, a constante elástica da mola equivalente, que, substituindo as duas produz o mesmo efeito será k_e = k + k  —  k_e =2k e seu período será T’ = 2pm/2k  —  T’ = 2p√m/k.1/√2.

T/T’ = √2  —  T’ = T/√2  — racionalizando  —  T’= T√2/2  Resposta C

13-  Como as duas molas de constantes k₂ estão em para, a mola equivalente terá constante k_e1 =30 + 30 = 60N/m. Então teremos:

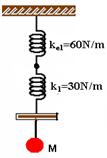
As duas molas acima estão em série, então a mola equivalente terá constante k_e, dada por: 1/k_e = 1/60 + 1/30  —  k_e = 20N/m,

que é a constante elástica total  equivalente do conjunto.

 

14- As 3 molas de constantes k₂ estão em paralelo e serão substituídas por uma única mola de constante k_e1=3k₂.

As duas molas de constantes k₁ também estão em paralelo e serão substituídas por um única mola de constante k_e2=2k₁

Então, teremos:

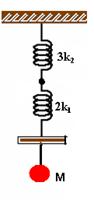
A mola resultante das duas acima, que estão em série, terá k_e, tal que: 1/k_e = 1/3k₂ + 1/2k₁  —  1/k_e = 2k₁ + 3k₂ / 6k₁.

K_e = 6k₁.k₂ / 2k₁ + 3k₂

O período desse sistema vale  —  T = 2p√m/6k₁.k₂ / 2k₁ + 3k₂  —  T = 2p√m(2k₁ + 3k₂)/6k₁.k₂

F = 1/T = 1/2p√6k₁.k₂ / m(2k₁ + 3k₂)

 

15- a) A mola inteira (mola equivalente) tem constante elástica k’=10N/m sendo que 1/k’= 1/k + 1/k +1/k, onde k é a constante elástica de cada parte.

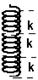
1/k’=3/k  —  1/12 = 3/k  —  k =36N/m

b) Paralelo  —  k­e=36 + 36 +36  —  k_e=108N/m  —  T=2p√m/k_e  —  T=2p√0,1/108  — T @ 6..10^-2.p s

c) Série  —  k_e=12N/m  —  T=2p√m/k_e  —  T=2p√0,1/12  —  T@ 18.10^-2.p s

 

16– a) Peso de cada massa  —  P=mg  —  P=0,01.10  —  P=0,1N. Como as molas são ideais, suas massas são desprezíveis.

Observe que a mola 1 está sujeita à força F=0,3N (são as 3 massas que estão deformando-a)

F₁=k₁.x₁  —  0,3=0,1.x₁  —  x₁ = 3cm

A mola 2 está sujeita à F=0,2N (apenas duas massas estão deformando-a)

F₂=k₂.x₂  —  0,2=0,1.x₂  —  x₂= 2cm

Mola 3  —  F₃=k₃.x₃  —  0,1=0,1.x₃  —  x₃= 1cm

b) mola 1 – L₁= 23cm

mola 2 – L₂= 22cm

mola 3 – L₃= 21cm

c) 6 cm

17- Soma (04 + 08) =12  Vide teoria

18- No momento em que o fio é cortado a massa mais próxima do teto ficará, neste instante, sujeita a uma força resultante de intensidade  igual a 2P= 2mg e, portanto, a uma aceleração descendente de 2g  —  o outro corpo neste instante estará sujeito ao seu próprio peso P=mg e logo a uma aceleração igual a g.

R- (01 + 08) = 09

19- A força de tração, o empuxo da água e o peso do corpo estão relacionados: E + T = P  —  d.g.V + T = P  —  T = P – d.g.V  —  T = 10 – 1000.10.0,0004 = 10 – 4 = 6 N  —  o trabalho é o produto da força pelo deslocamento  —  W=6.0,1 = 0,6 J  — 

R- C

20- a) Para instalar os 20 m de comprimento (L), o número n de passos de mola necessário é dado por  —  L = n × a + (n + 1) e  —  a = separação entre os anéis  —  e = diâmetro do fio (bitola)  —  L = comprimento do muro  —  20 = n 0,1 + (n + 1) 0,008  —  20 = 0,1n + 0,008n + 0,008  —  20 = 0,108n + 0,008  —  n ≈ 20 / 0,108  —  n ≈ 185  —  número de voltas N  —  N = n + 1 = 186  —  com as voltas compactadas e superpostas, a altura total é dada por  —  H = N e = 186 × 0,008 m ≈ 1,5 m  —  quantidade C de caixas necessárias  —  C ≥ 1,5/0,4 = 3,75  —  como o número de caixas deve ser inteiro  —  C_mínimo = 4

b) O comprimento inicial da mola vale L_o = 1,5 m e o comprimento final deverá ser L = 20 m  —  Lei de Hooke  —  F = k (L – L_o)  —  F = 5 (20 – 1,5) N = 92,5N  —  F = 92,5N 

21- Dados  —  x = 21 cm = 0,21 m  —  F = P = m g = 22,7(10) = 227 N  —  da lei de Hooke: F = k x  —  K=F/x=227/0,21  — 

K=1.080,95  —  K=1,081.10³N/m  —  R- E N/m 

R- E

22- Pela tabela  —  K=F_e/X=160/10=320/20=480/30=16N/cm  —  K=1.600N/m=1,6kN/m  —  R- B

23- As forças que agem sobre a bola e sua soma vetorial estão indicadas na figura  —  F_R=2F_ecosθ  —  cosθ=x/ℓ  —  F_e=-K(ℓ –

ℓ_o)  —  F_R=-2.K. (ℓ – ℓ_o).x/ℓ  —  F_R=-2K.(x –  (ℓ_o.x)/ℓ)  —  F_R=-2Kx(1 – ℓ_o/ℓ)  —  F_R=-2Kx(ℓ_o/√ (ℓ_o² + x²))  —  para chegar na aproximação do enunciado  —  ℓ_o/√ (ℓ_o² + x²) = ℓ_o/√ (ℓ_o² + x²)= ℓ_o/ℓ_o x  ℓ_o/√ (ℓ_o² + x²)=1/√(1 + x²/ ℓ_o²)  —  F_R=1/√(1 + x²/ ℓ_o²) ℓ_o/√ (ℓ_o² + x²)= (1 +  x²)=(1 + x²/ ℓ_o²)^-1/2=1 + (-1/2.x²/ ℓ_o²)  —  F_R=1 + (-1/2.x²/ ℓ_o²)=Ma  —  Ma= -2Kx{1 – (-1/2.x²/ℓ_o²) 1 + (-1/2.x²/ ℓ_o²)}  —  a= -Kx³)/Mℓ_o²  —  R- E

 

24-

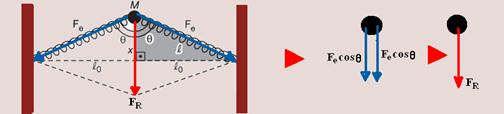
Como o sistema está em equilíbrio as intensidades da força P=mg e das forças elásticas F_e=k.d devem se igualar  —

P=2F_e  —  m.g=2.k.d  —  k=mg/2d  —  R- C.

25-

26-

 

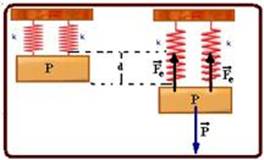
I- Falsa  —  quando a esfera atinge a mola, sua velocidade vai aumentando, enquanto houver resultante para baixo (P>F_e)  — a partir do instante em que as forças peso e elástica se anulam, a força elástica continua aumentando ficando maior que a força peso, a resultante agora é para cima, diminuindo a velocidade da esfera.

II. Falsa  —  a mola atinge sua máxima deformação quando a velocidade da esfera é nula (ela inverte o sentido de seu movimento e fica em repouso, para começar a voltar)  —  chamando esse ponto de C e colocando nele o nível zero de

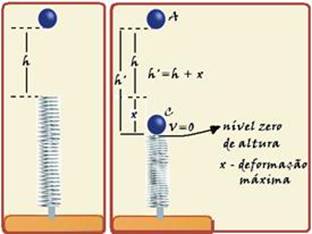
altura, a energia mecânica nele será  —  E_mC=mV²/2 + m.g.h + kx²/2=m.0²/2 m.g.0 + kx²/2  —  E_mC=kx²/2  —  E_mC=50x² (I)  —  no ponto mais alto (A) de onde a esfera e´abandonada (V=0), sua energia mecânica vale  —  E_mA=mV²/2 + m.g.h’=m.0²/2 + m.g.h=1.10.(6 + x)  —  E_mA=60 + 10x (II)  —  igualando (I) com (II)  —  50x² = 60 + 10x  —  5x² – x – 6=0  —  resolvendo essa equação  —  x=1,2m.

III. Correta  —  a velocidade é máxima quando F_e=P (veja I)  —  kx=mg  —  100.x=1.10  —  x=0,1m=10cm.

IV. Correta  — a velocidade é máxima quando x=0,1m (veja III)  —  chamando esse ponto de D e colocando nele o

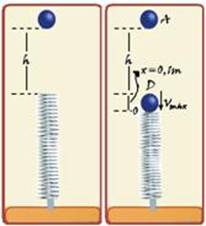
 nível zero de altura  —  E_mD=m(V_máx)²/2 + k.x²/2 + m.g.0=1.(V_máx)²/2 + 100.(0,1)²/2 + 0  —  E_mD=0,5 + 0,5(V_máx)² (I)  —  em A  —  E_mA=m.g.(h + x) + mV²/2=1.10.(6 + 0,1) + 0  —  E_mA=61J (II)  —  igualando (I) com (II)  —  61=0,5 + 0,5(V_máx)²  —  V_máx=√121  —  V_máx=11m/s.

V- Correta  —  como o sistema é conservativo, os atritos são desprezados e as forças são conservativas, a velocidade com que a esfera atinge a mola é a mesma com que ela deve retornar para atingir a mesma altura de h=6m  —  conservação da energia mecânica  —  A  —  E_mA=m.g.h=1.10.6=60J  —  quando atinge a mola (ponto B)  sua energia mecânica será  —  E_mB=mV²/2=1.V²/2  —  E_mA = bem  —  60 = V²/2  —  V=√(120)=2.(30)^0,5m/s.

R- D.

27- Como cada um dos tênis tem 3 molas, a pessoa em pé está apoiada sobre dois tênis, então você terá 6 molas associadas em paralelo  —  assim, cada mola suportará uma força de  —  P=m.g=84.10=840N/6  —  F=140N (força suportada por cada mola, que é a força elástica Fe)  —  Fe=k.x  —  140=k.4.10-3  —  k=140/4.10-3  —  k=35.103N/m  —  k=35kN/m  —  R- A

Voltar para os Exercícios