Força de resistência do ar – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Força de resistência do ar
01– R- A – vide teoria
02– R- C- vide teoria
03– D – vide teoria
04– Como ela cai com velocidade constante, está em equilíbrio dinâmico (força resultante nula). Assim, P=Fr=3,2.10-7N
Fr=K.V2 — 3,2.10-7=8.10-6.V2 — V=Ö(4.10-2) — V=2.10-1m/s R- B
05- O peso P do conjunto é o mesmo tanto para o pára-quedas aberto como fechado.
pára-quedas fechado – velocidade constante – F1=P — F1=K1.V12 — P=K1.V12 I
pára-quedas aberto – velocidade constante – F2=P — F2=K2.V22 — P=K2.V22 II
igualando I com II — K1.V12=K2.V22 — mas K2=100K1 — K1.V12=100K1.V12 — V22/V12=1/100 — V2/V1=1/10=0,1
06- a)
b) velocidade constante — Fr=P=mg=4.10 — Fr=40N Fr=K.V2 — 40=2,5.V2 — V=4m/s
07- a) A medida que o conjunto vai caindo a velocidade e a força de resistência do ar vão aumentando até que F fique igual a P.
A partir daí o conjunto entra em equilíbrio dinâmico e ele cai com velocidade constante. (a mesma que tinha quando F se igualou a P e a mesma com que ele chega ao solo).
b) F=P=mg=50.10=500N — F=500N F=b.V — 500=b.10 — b=50N.s/m
08- Como o exercício não se referiu a desprezar os atritos, existe ar e nesse caso a alternativa correta é a B
09- Calculando a constante K pelo gráfico — F=K.V — 4.10-4=K.2 — K=2.10-4Ns/m Após ter velocidade constante F=P
F=mg=10-4.10=10-3N — F=K.V — 10-3=2.10-4.V — V=10-3/2.10-4 — V=5m/s R-C
10- a) Como a caixa cai com velocidade constante, já foi atingido o equilíbrio e F = P =mg=0,2.10 — F=2N
b) Vamos calcular o intervalo de tempo Dt que a caixa demora para, em movimento vertical caie DS=2cm=2.10-2m, com velocidade constante V=10m/s.
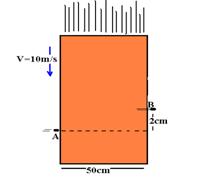
V=DS/Dt — 10=2.10-2/Dt — Dt =2.10-2/10 — Dt=2.10-3s. Mas, esse tempo é o mesmo que a bala, em movimento horizontal com velocidade Vb, demora para atravessar a caixa e percorrer DS=50cm=5.10=1m. — Vb=DS/Dt — Vb=5.10-1/2.10-3 —
Vb=250m/s
11- 1) Como a velocidade é constante a aceleração é nula (equilíbrio dinâmico).
2) Correta, pois como, nesse instante, a velocidade vertical de queda é nula a força de resistência do ar não existe e a força resultante sobre ele é a gravitacional (seu peso), puxando-o para baixo.
3) Sem ar, trata-se de uma queda livre com a=g=10m/s2. — V=Vo + g.t — V=0 + 10.10 — V=100m/s que multiplicado por 3,6 nos fornece 36km/h. Correta.
4) Errada, a força de resistência do ar é menor que a força da gravidade (peso) e vai aumentando até iguala-la e, a partir daí cai com velocidade constante.
12- a)A velocidade se torna constante a partir de t=10s quando y=325m (enunciado e gráfico). A partir daí, ele percorre DS=525-
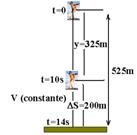
325=200 — DS=200m num intervalo de tempo Dt=14-10 — Dt=4s, com V constante de valor: V=DS/Dt — V=200/4 —
V=50m/s, que é a velocidade com que ele chega ao solo (velocidade limite).
b) R=K.V2 — R=P=m.g=75.10=750N — 750=K.(50)2 — K=0,3Ns2/m2
c) Quando sua velocidade for de 25m/s – V=25m/s e K=0,3Ns2/m2, a força de resistência do ar vale — R=K.V2 — R=0,3.252
R=187,5N — P=750N — FR=ma — P – R=ma — 750 – 187,5=75.a — a=7,5m/s2
13- R- D vide teoria
14- As membranas interdigitais das patas funcionam como pára-quedas aumentando a força de resistência do ar fazendo com que sua velocidade tenda a um valor limite, a partir da qual cairá com velocidade constante — R- A
15- FR=KV2 — K=FRV2=m.aV2=(m.V/t)/V2 — K=(m/t)/V — K=(kg/s)/(m/s) — K=kg/s x s/m — K=kg/m — R- D
16-Se você não domina a teoria desse exercício, atentamente as informações a seguir: Quando corpos se movimentam num fluido (ar ou água), além do peso que é constante surge também uma força, contrária ao movimento, que chamamos de força de resistência do ar (
), que depende da velocidade do corpo, de sua forma e da área de secção transversal em relação à direção do movimento nesse meio.
Assim, sobre um pára-quedista no ar, com o para quedas fechado, surgem sempre na direção do movimento (vertical), duas forças: seu peso (
) que é sempre constante, para baixo e a força de resistência do ar (
), que é variável e sempre para cima.
Sem pára-quedas ele deve manter sempre o corpo na horizontal para aumentar a resistência do ar.
No início da queda, quando a velocidade vertical é nula, = 
e sobre ele age apenas a força peso, acelerando-o para baixo (figura 1).
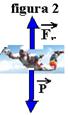
A partir daí, sendo > ele cai acelerando e sua velocidade vai aumentando e também, pois quanto maior a velocidade maior será (figura 2).
Chega um momento em que a intensidade de fica igual à intensidade da força peso e ele entra em equilíbrio dinâmico (força resultante nula 
) e sua velocidade vertical nesse instante é chamada velocidade terminal ou velocidade limite (que permanece a mesma até ele abrir o pára-quedas). Essa é a primeira velocidade limite . Observe que ela é maior para a pessoa mais pesada, pois para ela, como seu peso é maior, ele demora mais tampo para equilibrar a força de resistência do ar e sua velocidade será maior . Quando ele abre o pára-quedas, a área de contato com o ar aumenta, aumentando também a força de resistência do ar que fica maior que o peso (figura 4).
Como, agora, > ele desacelera diminuindo até que novamente eles se igualem = e o pára-quedista começa a cair novamente com velocidade constante (figura 5), que será novamente maior para a pessoa mais pesada, pelo mesmo motivo que o anterior.
Essa segunda velocidade limite que é a velocidade com que ele chega ao solo, sendo maior para o corpo mais pesado — R- E.
17- Primeira explicação — verdadeira — observe no gráfico que, entre t1 e t2 a velocidade é constante e, consequentemente a aceleração também será nula, assim como a força resultante, pois a força de resistência do ar anula a força peso.
Segunda explicação — verdadeira — quanto maior a velocidade, maior será a intensidade da força de resistência do ar.
Terceira explicação — falsa — como existe atrito com o ar o sistema não é conservativo e a energia mecânica não se conserva.
Quarta explicação — falsa — se a força resultante fosse para cima, a intensidade da força de resistência seria maior que a força peso e o pára-quedista subiria.
R- A.
18-
a) Observe a figura abaixo:
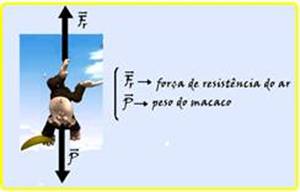
b) Durante a queda, a velocidade do macaco vai aumentando e, consequentemente a intensidade da força de resistência do ar (
) também, enquanto que o peso(
)é sempre o mesmo — a intensidade máxima da força de resistência do ar ocorre quando ela e o peso () se anulam e a força resultante sobre o macaco fica nula (
) — a partir daí o macaco cai sempre com velocidade constante, com P=Fr — . P=m.g=1.10 — P=10N — P=Fr — Fr=10N.
c) Quando o macaco atinge a vegetação ele tem velocidade de vi=30m/s e depois, ele pára (vf=0) — como o enunciado pede para desprezar o trabalho do peso (força gravitacional), a dissipação de energia mecânica se refere apenas à
variação de energia cinética — ∆Em=∆Ec=mVf2/2 – m.vi2/2=1.02/2 – 1.302/2 — ∆Em= – 450J — energia dissipada — ∆Ed=450J.