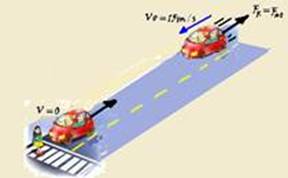
Força de atrito – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Força de atrito

 

01– Calculando as intensidades das forças de atrito:

estático  —  F_ate=μ_e.N==m_e.P=μ_e.mg=0,5.10.10  —  F_atr=50N – ele só entra em movimento se F for superior a 50N  —     dinâmico  —  F_atd=μ_d.N==m_e.P=μ_d.mg=0,3.10.10  —  F_atd=30N    

a) Se F=0, Fat=0, ele continua em repouso                

b) Se F=20N, F_ate=20N e ele continua em repouso    

c) Se F=40N, F_ate=40N e ele continua em repouso         

d) Se F=50N, F_ate=50N e ele continua em repouso, mas está na iminência de movimento.         

e) Se F=60N, ele entra em movimento e está acelerando com aceleração a tal que F_R=ma  —  F – F_atd=ma  — 

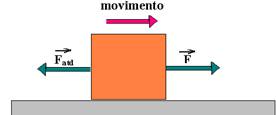
60 –   30=10a  —  a=3/10  —  a=3m/s² .

f) Como o bloco já está em movimento a força de atrito sobre ele é o dinâmico ou cinético e vale 30N.  —  F_r=ma  — 35 – 30=10.a  —  a=5/10  —  a=0,5m/s². Ele acelera com a velocidade aumentando de 0,5m/s em cada segundo.

g) Como F=30N e F_atd=30N, a força resultante sobre ele é nula e ele está em equilíbrio dinâmico, movendo-se em MRU.

h) Nesse caso a força resultante sobre ele é o F_atd=30N que o está freando com  —  F_atd=ma  —  30=10.a  —  a=3m/s² e sua

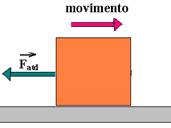
velocidade vai diminuindo de 3m/s em cada segundo, até parar.     

02– Pelo gráfico observamos que quando F=15N, a força de atrito estático é máxima e vale F_ate=15N. Qualquer força acima desse valor coloca o bloco em movimento. Quando F=30N, ele já entrou em movimento e o F_at sobre ele é o dinâmico e vale F_atd=10N (vide gráfico)  —  F_R=ma  —  30 – 10=5.a   —  a=4m/s²    —   F_ate=μ_eN=μ_eP=μ_emg  —  15=me.5.10  —  μ_e=15/50  —  μ_e=0,3

R- A

03- A única força que age sobre a caixa, na direção horizontal é a força de atrito dinâmico que é a força resultante, freando-o até parar.

V= V_o + a.t  —  0 = 10 + a.5  —  a= -2m/s² (negativo, pois está freando)  —  em módulo a=2m/s²  —  F_R=ma  —  F_atd=ma  — μN=ma  —  μP =ma  —  μmg=ma  —  μ=a/g  —  μ=2/10  —  μ=0,2  R- B

04– As forças verticais  e se anulam, sobrando apenas a força de atrito dinâmico que é a força resultante sobre ele.

 

V_o=72km/h/3,6=20m/s  —  Torricelli  —  V² = V_o² + 2.a.DS  —  0² = 20² + 2.a.50  —  a=-400/100  — a=-4m/s²  —  em módulo  —  a=4m/s²  —  F_R=F_atd=m.a  —  F_atd=10³.4  —  F_atd=4.10³N  —  V=V_o + a.t  —  0=20 + (-4).t  —  t=5s  —  F_atd=μ_dN=m_dP=μ_dmg — 4.10³=μ_d.10³.10  —  μ_d=4.10³/10⁴  —  μ_d=0,4

05- Calculando a intensidade da força de atrito dinâmico que age sobe cada bloco

A  —  F_atA=μ_A.N_A  —  F_atA=μ_A.P_A  —  F_atA=μ_A.m_A.g  —  F_atA=0,2.6.10  —  F_atA=12N       

B  —  F_atB=μ_B.N_B  —   F_atB=μ_B.P_B  —  F_atB=μ_B.m_B.g  —  F_atB=0,3.4.10  —  F_atB=12N  

Colocando as forças na direção do movimernto que é horizontal:

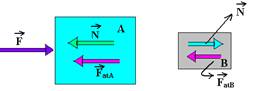
Bloco A  —  F_RA=μ_A.a  —  F – (N + F_atA)=m_Aa  —  60 – N – 12=6.a  —  48 – N=6.a  I

Bloco B  —  F_RB=m_B.a  —  N – F_atB=m_B.a  —  N – 12=4.a  II

Somando membro a membro I com II  —  36=10.a  —  a=3,6m/s²  —  N – 12=4.a  —  N=12 + 4.3,6  —  N=26,4N  R- A

06– Colocando as forças

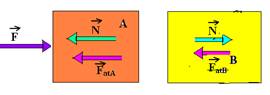
P_A=P_B=P

F_atA=μ_A.N_A  —  F_atA=μ_A.P  —  F_atA=0,5.P     

F_atB=μ_B.N_B  —   F_atB=μ_B.P  —  F_atB=0,5.P  

Bloco A —  F_R=m.a  —  F – (N + F_atA)=m.a  —  10 – N – 0,5P=m.a I

Bloco B  —  F_R=m.a  —  N – F_atB=m.a  —  N – 0,5P=m.a II  —  somando I com II  —  10 – P=2m.a  —  a=(10 – P)/2m III

Substituindo III em II  —  N – 0,5P = m(10 – P)/2m  —  N=0,5P + 5 – 0,5P  —  N=5N R-D

07– F_atA=μ.m_A.g  —  F_atA=m.2.10  —  F_atA=20m   —   F_atB=μm_Bg  —  F_atB=m.1.10  —  F_atB=10m

a) Colocando as forças:

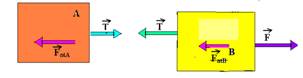
 Como os blocos estão com velocidade constante, estão em equilíbrio dinâmico e a força resultante sobre eles é nula  —bloco B  —  F_R=0 —  F – F_atB – T=0  —  18 – 10m – T=0  I   —   bloco A  —  F_R=0  —  T – 20m=0  II  —  somando I com II  —  18 – 30m=0  — m=0,6

b) T – 20m=0  —  T=20.0,6  —  T=12N

08– a) Fat_A=Fat_B=Fat_C=μMg   

Como a velocidade é constante o sistema está em equilíbrio dinâmico e a força resultante sobre cada bloco é nula, assim, a=0.

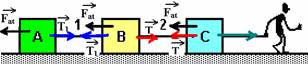
b) bloco B  — F_r=0  —  T=F_at + T₁  —  T= μMg + T₁ I      —   bloco A  —  F_R=0  —  T₁=Fat  —  T₁=μMg  II   — substituindo II em I  —  T=μMg

09– a) Como o caminhão e o caixote estão com velocidade constante (equilíbrio dinâmico) a força resultante sobre o caixote é nula e, se F_R=0, F_at também será nula.

b) A força resultante que age sobre o caixote, na direção do movimento é a força de atrito F_at que ele troca com a carroceria.

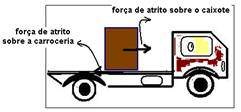
Sobre o caixote  —  F_r=m.a  —  F_at=m.a  —  μmg=m.a  —  0,25.10=a  —  a=2,5m/s²  —  a=2,5m/s²  —  V=V_o + a.t  —  0 = 20 – 2,5.t  —  t=20/2,5  —  t=8s

10- A intensidade da força de atrito estático entre as caixa e a carroceria vale F_ate=μN  —  F_ate=μP  —  F_ate=mg  —  F_ate=0,1.500.10  —  F_ate=500N (acima desse valor as caixas se movem).

No movimento acelerado  —  V=V_o + a.t  —  30=0 + a.20  —  a=1,5m/s²   —  F_R=m.a  —  F_R=500.1,5  —  F_R=750N ( como F_R>F_ate, as caixas se movem para trás e ficam juntas na parte traseira do caminhão).

No movimento uniforme, elas estão em equilíbrio dinâmico e F_R=0. Assim, elas não se movem e ficam juntas na parte traseira.

No movimento retardado  —  V=V_o + a.t  —  0=30 – a.40  —  a=3/4m/s²  —  F_R=m.a  —  F_R=500.3/4  F_R=375N (menor que 500N, portanto elas não se movem e ficam na parte traseira do caminhão) R- A

11- A força de atrito sobre cada bloco é a mesma e vale f

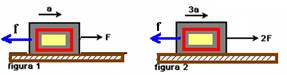
figura 1  —  F_R=m.a  F – f=m.a I    —    figura 2  —  F_R=m.a  —  2F – f=m.3.a II  —  multiplicando I por (-1) e somando membro a membro I com II  —  F=2ma III    —    substituindo III em I  —  f=ma IV    —    dividindo membro a membro IV por III  — 

f/F = 1/2

12- R- C (vide teoria)

13– a) Considerando os dois blocos como um corpo só de massa 3kg  —  F_R=m.a  —  4,5=3.a  —  a=1,5m/s².

b) colocando as forças de atrito que os blocos A e B trocam entre si e que constituem par ação e reação (mesma intensidade,

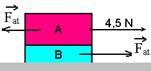
mesma direção e sentidos opostos) e aplicando F_R=m.a apenas no bloco B  —  F_R=F_at=1,2.1,5  —  F_at=1,8N  —  agora, aplicando F_R=m.a apenas sobre o bloco A, teremos  —  F_R=m.a  —  4,5 – F_at=1,6.1,5  —  F_at=1,8N  —  F_at=μN  —  F_at=μP  —  F_at=μmg  —  1,8=μ.1,8.10  —  μ=1,8/18  —  μ=0,1

14- a) F_R=(2,0 + 3,0).a  —  2=5.a  —  a=2/5  —  a=0,4m/s².

b) colocando as forças de atrito que os blocos trocam entre si

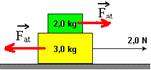
Bloco de baixo  —  F_R=m.a  —  2 – F_at=3.0,4  —  F_at=0,8N

15- A força de atrito é a mesma nos dois casos:

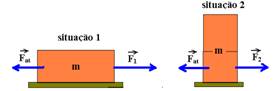
O F_at em cada situação é o mesmo, pois F_at=mP e m e P são os mesmos.

situação 1  —  F_R=m.a  — F₁ – F_at=ma  —  F₁=F_at + ma I    —-    situação 2  —  F_R=ma  —  F₂ – F_at=ma II  —  Observe em I e em II que F₁=F₂, portanto F₂/F₁=1 R- B

16- Cálculo da aceleração do sistema  —   F_R=m.a  —  12=(1 + 2,5 + 0,5).a  —  a=3m/s² (aceleração dos três blocos).

Forças que atuam no corpo C:

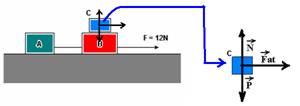
Peso de C, aplicado pela Terra, de intensidade p=mg  —  P=0,5.10com módulo 5,0 N.

Força normal para cima, aplicada por B sobre C, de intensidade N=5,0N (C está em equilíbrio vertical).

Força de atrito que B aplica sobre C  —  F_R=m.a  —  F_at=0,5.3  —  F_at=1,5N

Observação: As forças  e podem ser somadas vetorialmente e se tornarem uma única força de B sobre C que chamamos de

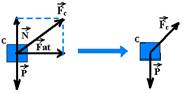
 força de contato  e que tem intensidade (F_C)²=(1,5)² + (5)²  —  F_C=5,2N

17- a) Quando o cartão é puxado pela força , horizontal e para a direita, ele aplica sobre a moeda uma força de atrito cinético (dinâmico) , puxado-a também para a direita.

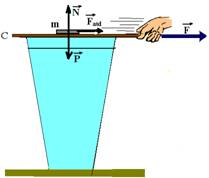
Sobre a moeda, além de ´(horizontal e para a direita) agem também as força verticais:  (peso da moeda) e (força normal exercida pelo cartão).

b) O Princípio da Inércia afirma que todo corpo em repouso, por inércia, tende a permanecer em repouso, mas somente se a força resultante sobre ele for nula e, no caso da moeda esse princípio não é válido, pois existe atrito ().

Vamos calcular a força de atrito estático  —  F_ate=μN  —  F_ate=μP  —  F_ate=mmg  —  F_ate=0,15.0,01.10  —  F_ate=0,15N (para qualquer valor de F maior que 0,15N, a moeda entra em movimento, ou seja, destaca-se do cartão.

Assim, se F for maior que 0,15N a moeda poderá cair dentro do copo e se F for menor ou igual a 0,15N, a moeda acompanhará o cartão e não se destacará dele.

18- Como entre o bloco A e o bloco B não há atrito, a força resultante, na direção do movimento, sobre o bloco A será  —  F_R=F_A= M_A.a_A  —  24=1.a_A  —  a_A=24m/s²

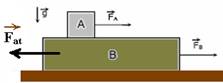
Entre o bloco B e o solo existe atrito que vale F_at=μN  —  F_at=μ (P_A + P_B)  —  F_at=0,2.50  —  F_at=10N  — bloco B  —  F_R=m_B.a_B  —  F_B – F_at=4.a_B  —  12 – 10=4.a_B  — a_B=0,5m/s²

Assim, a aceleração relativa entre A e B é de a=24 – 0,5  —  a=23,5m/s².

19-Colocando todas as forças que agem sobre o bloco e sobre a parede

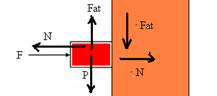
  equilíbrio na vertical  —  F_at=P=mg=3.10  —  F_at=30N  —  equilíbrio na horizontal  —  F=N  —  F_at=μN  —  30=0,2.F  —  F=30/0,2  —  F=150N  R- D

 

20-No equilíbrio estático na iminência de movimento, a força de atrito estática é dada por μeN, e se equilibra com o peso P. Na situação do exercício, a força normal N é tal que N = F. Assim, μeN = P implica em μe = P/F. Se μe < 1, logo 0 < P < F. R- A

21– Colocando todas as forças que se relacionam com a pessoa, a parede e o solo.

 

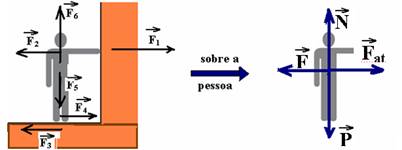
F₁ e F₂  —  forças trocadas entre a pessoa e a parede de intensidade 120N  —   F₃ e F₄  —   forças de atrito trocadas entre os pés da pessoa e o solo  —  F₅  —  peso da pessoa trocada com o centro da Terra e F₆, força normal que a pessoa troca com o solo.

Como a pessoa está em repouso, a força resultante é nula e as forças verticais e horizontais se anulam  R- D

22- Calculando a intensidade da força de atrito  que age sobre a pessoa  —  F_at=μN  —  F_at=μP  —  F_at=μmg  —  F_at=μ80.10  —

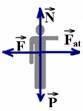
 F_at=800μ  —  mas, F_at=F=120N (equilíbrio horizontal)  —  120=800μ  —  μ=120/800  —  μ=0,15  R- A

23- Colocando as forças que agem sobre cada bloco na direção do movimento

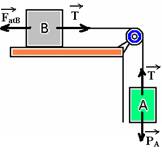
Observe que, como os blocos estão em equilíbrio  —  P_A=T e T=F_atB. Assim, F_atB=P_A    R- A

24- Colocando as forças sobre cada bloco na direção do movimento

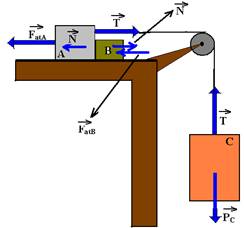
F_atA=μm_Ag  —  F_atA=0,2.3.10  —  F_atA=6N  —  F_atB=μm_Bg  —  F_atB=μm_Ag  —  F_atB=0,2.2.10  —  F_atA=4N  —  P_C=m_C.g  — P_C=7.10  —  P_C=70N

bloco C  —  desce  —  F_R=m_Ca  —  P_C – T=m_C.a  —  70 – T=7.a  I  —  bloco B  —  F_R=m_B.a  —  N – 4=2.a  II  —  bloco A   — F_R=m_A.a  —  T – N – 6=3.a  III   —   somando membro a membro I, II e II  —  70 – 10=12.a  —  a=5m/s²

A força de contato entre A e B é N  —  substituindo a=5m/s²  em II  —  N – 4=2.5  —  N=14N  R- B

25- Colocando o bloco de massa m sobre o bloco de massa 10kg e todas as forças que influem na tendência de movimento:

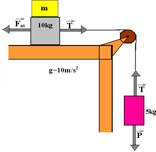
Como o sistema está em repouso, a força resultante sobre cada bloco é nula  —  bloco de massa 5kg  —  F_R=0  —  P=T=5.10  —  T=50N  —  blocos apoiados na superfície horizontal  —  F_at=T  —  μN=50  —  m(P_10kg + P_m)=50  —   0,2.(10 + m).10=50  — 

20 + 2m=50  —  m=30/2  —  m=15kg    (para qualquer m<15kg colocada sobre 10kg, o sistema se moverá no sentido horário).

26-   —  força que o bloco A troca com o bloco B  —   – peso do bloco B  —   – força de atrito que o bloco A aplica no bloco B, impedindo-o de escorregar.

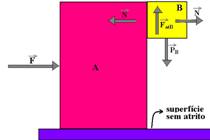
bloco B  —  equilíbrio vertical  —  F_atB=P=mg=0,4.10  —F_atB=4N  —  F_atB=μN  —  4=0,9N  —  N=4,4N

cálculo da aceleração de B em movimento horizontal para a direita onde a força resultante é  —  F_R=m_B.a_B  —   N=m_B.a_B  — 4,4=0,4.a_B  —  a_B=11m/s²  —  mas, para o bloco B não cair e acompanhar o bloco A eles devem ter a mesma aceleração, ou seja,

a_A=11m/s²  —  bloco A  —  F_r=m_A.a_A  —  F – N=m_A.a_A  —  F – 4,4=5.11  —  F=59,4N(para qualquer F>59,4N, o bloco B não cairá).

27- R –D Como o movimento é retilíneo uniforme, a força resultante sobre o caixote na direção do movimento (horizontal) é nula e , na vertical, a força peso e a reação normal da esteira se anulam. 

28- a) – peso da caixa  —  – força normal que a caçamba aplica sobre a caixa  —   – força de atrito trocada entre a caçamba e a caixa.

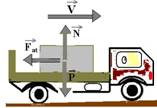
b) Essa força pedida é a força de atrito F_at  —   Cálculo da aceleração do caminhão por Torricelli  —  V²=V_o² + 2.a.DS  —  0²=(20)² – 2.a.100  —  a=2m/s²

Se a caixa não se mover em relação ao caminhão eles terão a mesma aceleração de 2m/s²e a força resultante  na direção horizontal vale  —  F_R=m.a  —  F_at=m.a  —  F_at=30.2  —  F_at=60N

29- Colocando as forças

 

 

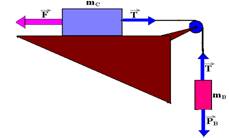
m_B  —  sobe com a=2m/s²  —  F_R=m_B.a  —  T – 50=5.2  —  T=60N  —  bloco C se move para a esquerda com aceleração de 2m/s²  —  F_R=m_C.a  —F – T=m_C.a  —  F – 60=10.2  —  F=80N

30- Colocando as forças e decompondo em  e em  :

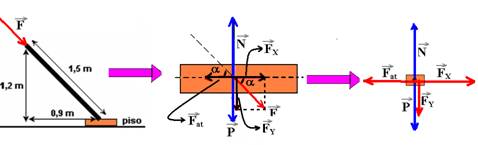
senα=1,2/1,5=0,8  —   cosα=0,9/1,5=0,6  —  F_X=Fcosα=F.0,6  —  F_X=0,6F  —  F_Y=Fsenα=F.0,8  —  F_Y=0,8F  —  P=mg=0,4.10  —  P=4N  —  estando o sistema em equilíbrio estático, F_X=F_at e N=P + F_Y  —  F_X=F_at  —  0,6F=μN  — 0,6F=μ (P + F_Y)  —  0,6F=1/8.(4 + 0,8F)  —  0,6F=4/8 + 0,8F/8  —  0,6F=0,5 + 0,1F  —  0,5F=0,5  —  F=1N (para qualquer valor de F<1N, a vassoura não se deslocará).

31- Como F_at=μN, e como m é constante, das alternativas, a única força capaz de diminuir a força de com pressão N da caixa com o chão é a C

32- Colocando as forças e decompondo em  e 

 

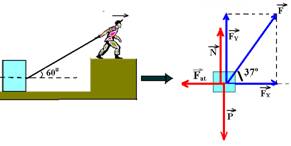
P=mg=42.10  —  P=420N  —  F_X=Fcos60^o=F.0,5  —  F_X=0,5F  —  F_Y=Fsen60^o=F.√3/2  —  F_Y=0,85F

No equilíbrio estático temos, na horizontal F_at=F_X e na vertical, P=N + F_Y  —  N=P – F_Y  —  F_at=F_X  —  μN=0,5F  —  μ (P – F_Y)= 0,5F  —  0,4(420 – 0,85F)=0,5F  —  168 – 0,34F=0,5F  —  0,84F=168  —  F=200N (qualquer valor acima de 200N desloca o bloco) R- C

33-Colocando as forças apenas na direção do movimento (horizontal):

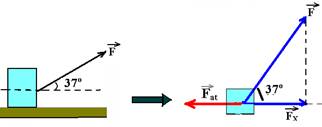
Como o movimento é na horizontal, vamos decompor  apenas em   —  F_X=Fcos37^o  —  F_X=0,8F. 

Na horizontal  —  F_R=ma  —  F_X – F_at=ma  —  0,8F – 0,6=2,0.0,1  —  F=0,8/0,8  — F=1,0N  R- B

34- a) como os corpos estão em movimento e como m_B>m_A, o sistema tem que se mover no sentido horário (A sobe e B desce). Colocando as forças:

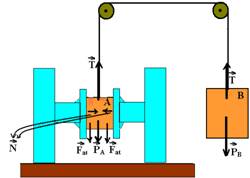
– força horizontal que cada um dos mancais exerce sobre o corpo A  —   – força de atrito que cada um dos mancais exerce sobre o corpo A tentando impedi-lo de subir e F_at=mN  —  corpo A – sobe  —  F_R=m_A.a  —  T – P_{a­  –} 2F_at=m_A.a  —  T – m_Ag – 2μN=m_A.a I  —  corpo B – desce  —  F_rm_B.a  — P_B – T=m_B.a  —  m_Bg – T=mB.a II  —  somando membro a membro I com II  —

m_Bg –  m_Ag – 2mN=m_A.a + m_B.a  — ( m_B – m_A)g – 2μN=(m_A + m_B)a  —  a=(m_B – m_A)g – 2μN /( m_A + m_B)

b) Se a velocidade é constante os corpos A e B estão em equilíbrio dinâmico e a força resultante sobre eles é nula.

corpo A  —  F_R=0  —  T = P_A + 2F_at  —  T=m_Ag + 2μN I  —  corpo B  —  F_R=0  —  T=P_B  —  T=m_Bg II  —  substituindo II em I  —  m_Bg =m_Ag + 2μN  —  N=(m_B – m_A)g /2μ

35- a) continua em repouso

b) Sobre o bloco B não existe nenhuma força horizontal

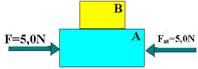
36- Colocando as forças sobre cada bloco

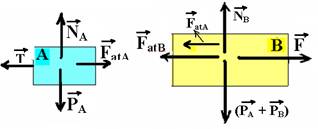
F_atA=μ_A.N_A  —  F_atA=μ_A.P_A  —  F_atA=0,25.100  —  F_atA=25N   —   como o sistema está repouso  —  bloco A  —   F_RA=0  —  T=F_atA=25N   —   bloco B  —  F=F_atB + F_atA  —  125=F_atB + 25  —  F_atB=100N  —  F_atB=μ (P_A + P_B)  —  100=μ.300  —  μ=1/3

37- Como o coeficiente de atrito é o mesmo e o peso de cada bloco é também o mesmo a força de atrito entre A e B vale F_atA=μN  —  F_atA=μP=F_at e entre B e o chão vale F_atB=μN=m(P_A + P_B)= μ2P  —  F_atB=2μP  —  F_atB=2F_at.

Colocando todas as forças, em cada caso:

             

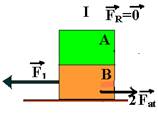
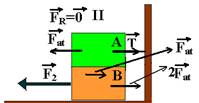
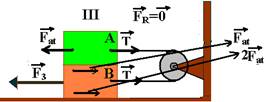
Situação I  —  A- nenhuma força e B – F₁=2F_at  —  situação II  —  A – T=F_at e B –F₂=3F_at  —  situação III  —  A – T=F_at e

B – F₃=4F_at 

F₂/F₁=3F_at/2F_at  —  F₂/F₁=1,5  —  F₃/F₁=4F_at/2F_at  —  F₃/F₁=2

38- Vamos chamar de L’, comprimento total do pano e de L’ – L o comprimento da parte pendente. Como o pano é de constituição homogênea, sua densidade é a mesma.

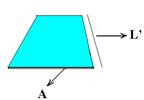
d=m_t/V_t  —  d (densidade) – m_t (massa total) – V_t (volume total)  —  m_t=d.V_t  —  m_t=d.(A.L’), sendo A (área se seção transversal, espessura do pano) e L’ (comprimento total do pano)

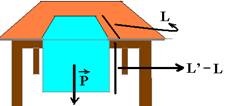
massa apoiada – m_a=d.A.L e massa pendente – m_p=d.A.(L’ – L)

– peso da parte pendente  —  P=m_pg (m_p, massa da parte pendente)  —  a força de atrito entre o pano de comprimento L e a mesa está segurando o peso da parte pendente de comprimento (L’ – L), ou seja, F_at=P  —  μm_ag= m_pg  —  μ.d.A.L.g=d.A.(L’ – L).g  —   0,5.L=(60 – L)  —  1,5L=60  —  L=40cm R- A

39- Colocando as forças

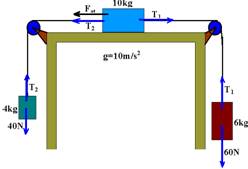
Observe na figura que a tendência de movimento é no sentido horário e, no bloco de massa 10kg a força de atrito estático é para a esquerda (contrário à tendência ao movimento).

Todos os blocos estão em repouso  —  bloco de massa 4kg  —  T₂=40N  —  bloco de massa 6kg  —  T₁=60N  —bloco de massa 10kg  —  T₁=T₂ + F_at  —  60=40 + F_at  — F_at=20N

40- Nas rodas com tração a força de atrito é a favor do movimento e nas rodas sem tração, contrária ao movimento. R- C

41- Nas rodas com tração a força de atrito é a favor do movimento e nas rodas sem tração, contrária ao movimento. R- B

42- I – A    II – C    III – D     IV – B   (vide resolução do exercício anterior)

43-  a) Fat=F_R=ma=3.10³.3  —  F_at=9.10³N   b) Para o bloco não escorregar F_R=F_at  —  ma=μmg  —  a=mg=0,4.10  —  a=4,0m/s²

44- a)Colocando as forças no imã-bonequinha:

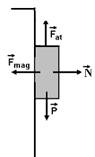
 – força peso, vertical e para baixo aplicada pela Terra  —  – força magnética aplicada pelo metal da parede da geladeira, atraindo o imã para ela  —   – força normal de compressão trocada entre a geladeira e o imã  —   – força de atrito entre a geladeira e o imã

b) equilíbrio vertical  —  F_at=P  —  μN=mg  —  0,5.N=0,02.10  —  N=0,2/0,5  —  N=0,4N  —  equilíbrio horizontal  —  F_mag=N=0,4N

45- Cálculo da intensidade força de atrito F_at em cada bloco:

F_atA=μm_Ag=0,1.4.10  —  F_atA=4,0N  —  F_atB=μm_Bg=0,1.2.10  —  F_atB=2,0N  —  F_atC=μm_Cg=0,1m_C10  —  F_atC=m_C —  F_atA=4,0N  —  F_atB=μm_Bg=0,1.2.10  — F_atB=2,0N  —  F_atC=μm_Cg=0,1m_C10  —  F_atC=m_C

a=2,0m/s²

Colocando as forças na direção do movimento:

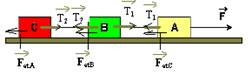
bloco A  —   F_R=m_Aa  —  30 – T₁ – 4=4.2  —  T₁=18N  —  bloco B  —  F_R=m_Ba  —  18 – 2 – T₂=2.2  —  T₂=12N  —  bloco C  —

F_R=m_Ca  —  12= m_C.2  —  m_C=6kg    —  F_RB=18 – 14=4N

1 – F; 2 – V; 3 – V; 4 – F; 5 – V

46- F=F_at=μN  —  360=0,2.N  —  N=1,8.10³N

47- Sobre o bloco B, na direção do movimento agem as forças F_at1=μN  —  F_at1=μP_A  —  F_at1=μm_Ag  —  F_at1=0,3.7.10  —  F_at1=21N, que é a ação de A sobre B e F_at2=μN  —  F_at2=m(P_A + P_B)  —  F_at2=0,3.(70 + 70)  —  F_at2=42N que é a reação de C sobre B.

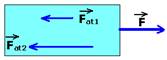
Como o bloco B se move com velocidade constante, F_RB=0  —  F=F_at1 + F_at2  —  F=21 + 42  —  F=63N

48-

48-a) Distância D, percorrida com velocidade constante V_o

V=DS/Dt  —  V_o=D/2

Distância D, percorrida com velocidade variando de V_o para 0, com desaceleração -a, no tempo t. 

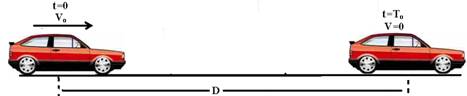
Torricelli  —  V²=V_o² + 2.a.∆S  —  0²=V_o² + 2.(-a).D  —  0²=(D/2)² – 2.a.D  — a=D/8  —  V=V_o + a.t  —  0=V_o + (-a).t — 0=D/2 – (D/8).t  —  t=4s

b) Relação entre a e V_o  —  a=D/8  —  V_o=D/2  —  V_o=4a  —  Trata-se de uma função do 1^o grau e o gráfico é uma reta, que é definida por apenas dois pontos, como por exemplo:

Quando a=0, V_o=0 (0,0) e quando a=10m/s², V_o=4.a  —  V_o=4.10  —  V_o=40m/s (40,10).

Colocando no gráfico:

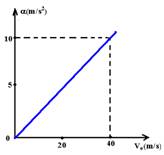
c) F_R=F_at  —  ma=μmg  —  a=0,6.10  —  a=6m/s²  —  quando a=6m/s², V_o=V_M e , pelo gráfico V_M»23,5m/s

 

49- No Bloco A na direção horizontal e sentido da força F é verdadeiro escrever  —  F_R = m.a  —  F – F(elástica) – F(atrito) = m.a  —  F – k.x – μ.m.g = m.a  —  60 – 800.x – 0,4.6.10 = 6.a  —  60 – 800.x – 24 = 6.a  —  36 – 800.x = 6.a  —  bloco B nas mesmas condições já citadas  —  F_R = m.a  —  F(elástica) – F(atrito) = m.a  —  k.x – μ.m.g = m.a  —  800.x – 0,4.4.10 = 4.a  — 

800.x – 16 = 4.a  —  resolvendo, por adição, o sistema formado pelas duas equações  —  36 – 800.x = 6.a  —  800.x – 16 = 4.a  —  36 – 16 = 10.a  —  10.a = 20  —  a = 20/10= 2 m/s²  —  800.x – 16 = 4.a  —   800.x = 16 + 4.2 = 16 + 8 = 24  —   x =24/800  —  x= 0,03 m = 3 cm  —  R- A

50- A máxima distância (d) do bloco à parede ocorre quando a força de atrito máxima (F_atmax) tem a mesma intensidade da força

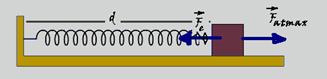
elástica (F_e). F_atmax=F_e=μP=Kx  —  x=μP/K=0,4.30/20  —  x=0,6m  —  R- C

51- As ranhuras tornam o piso mais áspero, aumentando o coeficiente de atrito.   

R- A

52- Se F=F_at, a resultante das força é nula e ao caixa se move em movimento retilíneo e uniforme  —  R- D

53- Dados: m = 120 kg; g = 10 m/s²; μ = 0,8; F/A= 30 N/cm²; N = P = 1.200 N  —  para colocar a caixa em movimento o operador tem que vencer a força de atrito  —  F_op = F_at = m N  —  0,8 (1.200) = 960 N  —  como ele está usando os dois braços, cada braço aplica então  —   F = F_op/2=480 N  —  F/A=30  —  480/A=30  —  A=16cm²  —  uma das proteínas responsáveis pela contração das miofibrilas é a actina  —  R- A

54- Como o movimento é uniforme, a resultante tangencial é nula  —  assim, a componente de atrito tem a mesma intensidade da força motriz; e como o movimento é horizontal, a componente normal tem a mesma intensidade do peso  —  dados: F_motriz = 2.000 N  —   m = 200 kg  —   g = 10 m/s²  —  F_atc=F_motriz=2.000N  —  N=P=mg=2.000N  —  F_atc=2.000=μ_cN  —  μ_c.2.000=2.000  —

μ_c=1  —  R- A

55- Dados  —   x₁ = 2 cm; x₂ = 10 cm  —  observe as figuras abaixo onde foram colocadas as forças nas duas situações  — 

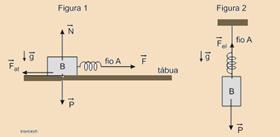
Na Figura 1, o bloco está na iminência de escorregar. A componente de atrito   é máxima e, como o bloco ainda está em repouso, ela tem a mesma intensidade da força elástica .  Pela mesma razão, a componente normal  tem a mesma intensidade que o peso do bloco  —  sendo k a constante elástica da mola, m a massa do bloco e g a intensidade do campo gravitacional, temos  —  N = P = m g  (I)  —  F_at = F  —  μ N = k x₁  (II)  —  substituindo (I) em (II)  —  μ m g = k x₁   (III).

Na Figura 2, o bloco também está em repouso  —  assim, a nova força elástica  equilibra o peso  —  F_el = P  —  k x₂ = m g (IV)  —  substituindo (IV) em (III)  —  m k ­x₂ = k x₁Þ  m =x₁/x₂=2/10  —  m = 0,2  —  R- B

56- Dados  —  g = 10 m/s²  —   μ_e = 0,60  —   μ_c = 0,80  —   m = 1.200 kg  —   força que a pista exerce no veículo tem duas componentes  —  normal  e  atrito   —  supondo que a frenagem ocorra em pista horizontal, a componente normal   da força que a pista aplica no veículo tem intensidade igual à do seu peso   —  N = P = m g = 12.000 N  —   componente de atrito estático máxima  —   F_atmax= μ_e N = 0,8 (12.000)  —   F_atmax = 9.600 N  —  a componente de atrito cinético: F_atc  = μ_c N = 0,6. (12.000)  —   F_atc = 7.200 N  —  R- D       

57- Na iminência de a caixa entrar em movimento, tem-se que as componentes horizontal e vertical da força resultante agindo sobre ela são nulas  —  assim, para a componente horizontal, Fcos(θ) = F_{ate max}=μ_eN  —  N e F_{ate max} denotam, respectivamente, os módulos da força normal e de atrito estático máxima nessa situação  —  componente vertical  —   N + Fsen(θ) = P  —  combinando essas duas equações, obtém-se que F = μ_eP/[cos(θ) + μ_e sen(θ)]  —  R- A

58- Na figura estão colocadas as forças que atuam sobre cada bloco  —  o bloco P está em equilíbrio na vertical (não cai)  — 

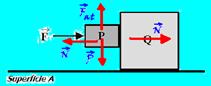
F_at=P  —  μN=mg  —  N=mg/μ (I)  —  para que o bloco P não caia, ele deve se mover na horizontal com a mesma aceleração que a do bloco Q  —  bloco P  —  F – N=ma (II)  —   bloco Q  —  N=Ma (III)  —  (II) com (III)  —  F=(M + m).a (IV)  —  (I) em (III)  — 

Mg/μ=Ma  —  a=mg/μM (V)  —  (V) em (IV)  —  F=(M + m).mg/μM  —  F=mg/μM.(M + m)  —  R- B

59- F_R=F_at=μN= μP= μmg=0,02.20.10  —  F_R=4N  —  F_R=ma  —  4=20a  —  a=0,2m/s²  —  Torricelli  —  V²=V_o² + 2.a.ΔS  — 

0²=V_o² + 2.(-0,2).45  —  V_o=√18≈4,2m/s  —  V=V_o + at  —  0=4,2 – 0,2t  —  t≈21s  —  R- C

 

60-

01) Correta

02) Correta

04) Falsa  —  constata-se experimentalmente que F_atemax>F_atc e que μ_e>μ_c, pois as reentrâncias e saliências das superfícies em contato estão mais encaixadas com o corpo em repouso, dificultando mais a movimentação.

08. Falsa  —  F_at=μ.N  —  μ=F_at (força-medida em N)/N (também força-medida  em N)  —  o coeficiente de atrito é uma grandeza adimensional, ou seja, não tem unidades.

16. Falsa  —  é a força de atrito estático máxima que é sempre maior que a força de atrito cinético.

Corretas: 01 e 02  —  soma=03.

61-

Os freios antitravamento (ABS, anti-lock braking system) ajudam a parar melhor  —  eles previnem o travamento das rodas e proporcionam uma distância de frenagem mais curta em superfícies escorregadias, evitando o descontrole do veículo  —  ele mantém as rodas sempre na iminência de deslizar, aproveitando melhor o atrito estático máximo, que é maior que o atrito cinético (de deslizamento)  — R- B.

62–

Cálculo da aceleração de retardamento do carro    —  V_o=54km/h/3,6=15m/s  —  V=0 (pára)  —  t=5s  —  V= V_o + a.t  —  0

= 15 + a.5  —  a= – 3m/s² (o sinal negativo de a significa que o carro está freando)  —  em módulo  —  a=3m/s²  —  depois que ele acionou os freios a intensidade da força resultante sobre o carro é a própria força de atrito  —  F_R=F_at  —  m.a = μ.N  —  m.a = μ.m.g  —  3= μ.10  — 

μ = 0,3  —  R- A

63-

Decompondo a força  em sua componente horizontal  e vertical    —  F_x=Fcos37^o=50.0,8  —  F_x=40N  —  F_y=Fsen37^o=50.0,6  —  F_y=30N  —  colocando as forças peso  (vertical e para baixo), a força normal (vertical e para cima) e

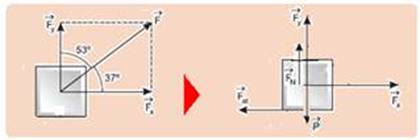
a força de atrito  (contrária ao movimento ou à sua tendência)  —  equilíbrio na vertical  —  P = F_y + F_N  —  50=30 + F_N  —  F_N=20N  —  F_at=μF_N=0,6.20  —  F_at=12N  —  na horizontal existe força resultante, pois F_R=F_x – F_at  —  F_R= 40 – 12  —  F_R=28N  —  F_R=m.a  —  28=5.a  —  a=5,6m/s²  —  R- D

64-

Colocando todas as forças (figura) que influem no movimento ou na sua tendência  — força de atrito  — 

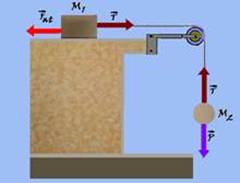
F_at=μN=μM₁.g  —  F_at=μ.10.10  —  F_at=100μ  —  como o sistema está em equilíbrio estático (repouso) a força resultante sobre cada corpo é nula  —  F_at=T  —  100μ=T (I)  —  como o bloco M₂ também está em repouso  —  T=P=M₂.g=5.10  —  T=50N II)  —  substituindo (II) em (I)  —  100μ=50  —  μ=0,5  —  R- C

65-

a) As forças que agem sobre o conjunto imã-grampo são  —   – força peso, vertical e para baixo, aplicada sobre o conjunto

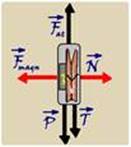
pela Terra  —   – força de tração no fio, vertical e para baixo, aplicada sobre o conjunto pela massa M pendurada  —  – força de atrito, trocada entre o conjunto  e a parede da geladeira, vertical e para cima, contrária ao movimento ou à sua tendência  —   –  força magnética, horizontal e que atrai o conjunto para a esquerda, é de atração magnética entre o imã e a parede da geladeira  —   – força normal, horizontal e para a direita, reação da parede da geladeira sobre o conjunto.

b) Se o conjunto não deve cair a força resultante sobre ele tanto na vertical como na horizontal deve ser nula  —  equilíbrio na vertical  —

F_at=P + T  —  P=m_og  —  T=Mg  —  F_at=μ_eN  —  μ_eN = m_og + Mg (I)  —  equilíbrio na horizontal  —  F_M=N (II)  —  (II0 em (I)  —  μ_eF_M = m_og + Mg  —  Mg = μ_eF_M – m_og  —  M= (μ_eF_M – m_og)/g ou M= μ_eF_M/g – m_o —  para esse valor de M o conjunto está na iminência de cair  —  para qualquer valor de M menor que esse, o conjunto não cai.

 

Voltar para os exercícios