Resolução Energia Mecânica

Resolução comentada dos exercícios de vestibulares sobre

Energia Mecânica

 

 

 01–Como não existe atrito a energia mecânica se conserva e onde a energia cinética é máxima (ponto R), a velocidade é máxima e a energia potencial gravitacional é mínima (altura mínima). Np ponto P a energia cinética é mínima (menor velocidade) e a energia potencial gravitacional é máxima (maior altura). R- B

02-Como a energia mecânica se conserva, a energia mecânica em P, que é a cinética (m.v²/2) mais a potencial gravitacional (m.g.h) é a mesma que chega à turbina. R- A

03- V=720km/h/3,6=200m/s — h=3.103m — Em=70.106J — Em=m.v2/2 + m.g.h — 70.106=m.(200)2/2 + m.10.3.103 — 70.106=m.4.104/2 + m.3.104 — m=70.106/5.104 — m=1.400kg —R- B

04- Cálculo da velocidade com que ela chega ao solo  —  V_o + g.t=0 + 10.4  —  V=40m/s  —  como se despreza a resistência do ar, o sistema é conservativo e a energia mecânica é a mesma em A e em B.

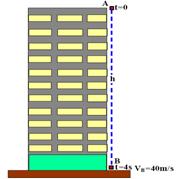
E_mA=m.V_A²/2 + m.g.h=m.0²/2 + m.10.h  —  E_mA=10.m.h  —  E_mB=m.V_B²/2 + m.10.0  —  E_mB=m.40²/2=800m  —  E_mA= E_mB  —  

10mh=800m  —  h=80m R- C

05- Se a velocidade é constante, a energia cinética é constante. Como a altura diminui a energia potencial gravitacional também diminui  R- B

06- Observe na figura abaixo:

E_mA=m.V_A²/2 +mgh=m(29/3,6)²/2 + 0= 32,45m —  E_mB =m.V_B²/2 + mgh=0 + m.10.h=10mh  —  E_mA=E_mB     —  32,45m=10mh  —  h=32,45/10  —  h=3,245m  R- D

07- R- C

08- A menor velocidade que ele deve ter no ponto A deve somente ocorrer se ele chegar em B com velocidade nula.

Pela conservação da energia mecânica  —  E_mA=E_pA + E_cA=mgh + mV²/2=m.10.8 + m.V²/2=80m + mV²/2  —  E_mB = mgh=m.10.13=130m  —  E_mA=E_mB  —  80m + mV²/2=130m  —  V²/2=50  —  V=10m/s 

09- antes de atingir a mola – E_ma=m.V²/2 – depois de comprimir a mola e parar (v=0), quando a compressão é máxima – E_md=kx²/2 –

E_ma=E_md  —  mV²/2=kx²/2  —  4.100/2=1.000.x²/2  —  x=0,4m=40cm  R- E

10- a) kx²/2=mV²/2  —  8000.(2.10^-2)²/2=0,2.V²/2  —  V²=32.10^-1/2.10^-1=16  — V=4,0m/s

b) mV²/2=mgh + mV²/2 —  8=10h + 4/2  —  h=0,6m

11- Colocando os pontos A, B e C na figura:

 

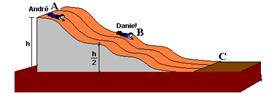
André – ponto A – como V=0 só tem energia potencial gravitacional  —  E_mA=E_pA=m.g.h  —  ponto C – como h=0 só tem energia cinética  —  E_mC= E_cC  —  sistema conservativo – E_mA=E_mC  —  E_cC=m.g.h  

Daniel – – ponto B – como V=0 só tem energia potencial gravitacional  —  E_mB=E_pB=2m.g.h/2=m.g.h  —  ponto C – como h=0 só tem energia cinética  —  E_mC= E_cC  —  sistema conservativo – E_mB=E_mC  —  E_cC=m.g.h  

Portanto, ao chegarem ao solo ambos terão a mesma energia cinética.

A energia cinética E_c com que ambos chegam ao solo é a mesma, assim:

André – E_c=mV_A²/2 – V_A=Ö2E_c/m

Daniel – – E_c=2mV_D²/2 – V_D=ÖE_c/m

Portanto, ao chegarem ao solo terão velocidades diferentes  —  R- D

12- Observe a figura abaixo:

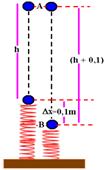
No ponto A só existe  energia potencial gravitacional, pois a cinética é zero  —  E_mA= E_pA=m.g.(h + Dx)=0,2.10.(h + 0,1)=2h + 0,2

E_mA=2h + 0,2  —  no ponto B (nível zero de altura), a energia potencial gravitacional (h=0) e a energia cinética (V=0) são nulas, existindo aí apenas energia potencial elástica  —  E_mB=k(Dx)²/2=1.240.(0,1)²/2=6,2  —  E_mB=6,2J  —  como o sistema é conservativo, E_mA = E_mB  —  2h + 0,2=6,2  —  h=3m

13- Vamos descrever todas as características deste movimento, desde o início, até quando a velocidade é máxima. (desprezando-se os atritos):

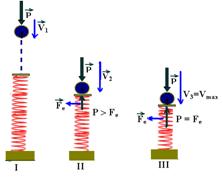
 I – a esfera é abandonada do repouso (V­o­=0) e cai sujeita apenas à força peso, com velocidade de intensidade V₁, que vai aumentando devido apenas à aceleração da gravidade, até atingir a mola.

II – ao atingir a mola, começando a comprimi-la, surge a força elástica () que se opõe ao peso (). A intensidade de   vai aumentando, diminuindo a intensidade da força resultante que é para baixo, fazendo com que V₂ aumente cada vez menos, até chegar à situação III.

III– nesta situação as intensidades das forças elástica e peso tornam-se iguais (P=F_e), quando a velocidade de queda torna-se máxima

  Veja na figura abaixo as condições do exercício:

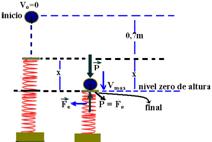
Na situação final  —  F_e=P  —  k.x=m.g  —  200.x=4.10  —  x=0,2m  —  toda energia mecânica do início (E_mi=mgh) é transformada em E_mf=E_pe + E_cmax na situação final   E_mi=E_mf  —  mgh=kx²/2 + mV_max²/2  —4.10.0,9=200.(0,2)²/2 + 4.V_max²/2  —

36= 4 + 2V_max²/2  —  V²=16  —  V=4m/s  R- B

14- Observe a figura abaixo:

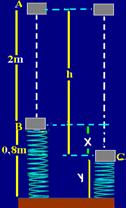
Tomando o ponto C como nível zero de referência para as alturas, a energia mecânica em A, onde a energia cinética é zero, será E_mA=m.g.(2 + x)=0,5.10.(2 + x)=10 + 5x —  considerando o sistema conservativo, a energia mecânica em C, onde a energia potencial gravitacional é nula (h=0) e a cinética também (menor comprimento,V=0) será somente a energia potencial elástica  —  E_mC=k.x²/2=100.x²/2=50x²  —  E_mA=E_mC  —  10 + 5x=50x²  —  10x² –x -10=0  —  D=B² – 4.A.C=1 + 80=81  —  ÖD=9  —

X=1±9/20 – x₁=10/20=0,5m – x₂ é negativo e não satisfaz  —  o menor comprimento da mola é y=0,8 – x=0,8-0,5  y=0,3m

15- Esse sistema massa-mola constitui um oscilador harmônico simples, de características:

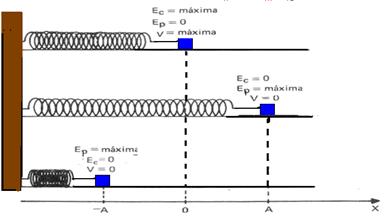
* A energia mecânica é sempre constante no MHS e vale E_m= kA²/2  ou  E_m=E_c + E_p  ou   E_m=kx²/2 + m.v²/2

* Nos extremos onde v=0 e o módulo de x é A, temos que  — E_m=E_c + E_p  — E_m= 0 + k.A²/2  —  E_m=k.A²/2 = constante

* No ponto médio 0, onde o módulo de v é máximo e x=0, temos que  —  E_m=E_c + E_p  —  E_m=mv²/2 + 0  —  E_m=mv²_max/2=const.

Cálculo da energia mecânica num dos extremos  —  E_me=k.A²/2=800.(0,5)²/2=100J  (constante)  —  no ponto P, onde E_c=E_p  —

E_me=E_c + E_p  —  100=E_c + E_c=2E_c=2.mV²/2=2.1.V²/2  —  100=V²  —  V=10m/s R- A 

16- Observe a figura abaixo:

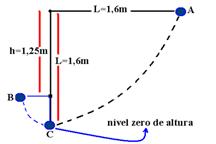
E_mA=m.g.h=m.10.1,6=16m  —  como o sistema é conservativo, E_mC também vale E_mC=16m  —  E_mB =m.g.(L-h) + mV²/2=m.10.0,35 + mV²/2=3,5m + mV²/2    —  E_mC =  E_mB  —  16m=3,5m + mV²/2  —  12,5=V²/2  —  V=5m/s

17- a) Energia mecânica em A  —  E_mA=mV_A²/2 + mgh=2V_A²/2 + m.g.0=10²  — E_mA=100J  —  energia mecâncica em B  —  E_mB =m.g.h + mV_B²/2=2.10.R + 2.V_B²/2=40 + V_B²  — E_mB=20 + V_B²  —  E_mA = E_mB  —  100=40 + V_B²  —  V_B=√60m/s  —  aceleração centrípeta – a_c=V²/R=(√60)²/2  —  a_c=30m/s²

b) Energia mecânica em C – E_mC=m.g.2R + m.V_C²/2=2.10.4 + 2V_C²/2=80 + V_c²  —  E_mC=80 + V_C²  —  E_mA=E_mC  —  100=80 + V_c²  —  V_c=√20m/s 

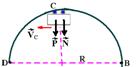
Quando o carrinho passa por C com velocidade de Ö20m/s, duas forças para baixo agem sobre ele, seu peso  e a reação da parte superior da superfície   — força resultante centrípeta em C – F_RC=m.V_C²/R  —  N + P= m.V_C²/R  —  N + 2.10=2V_C²/2  —

N + 20=(√20)²  —  N=20 – 20  —  N=0

18- a) Energia mecânica no início do movimento E_mi=m.V_i²/2 + m.g.h=0 + 0,2.10.0,4  — E_mi=0,8J  —  Energia mecânica no ponto X E_mX=E_pX + E_cX=0 + E_cX=E_cX  —  E­_mi=E_mX  —  0,8=E_cX  —  E_cX=0,8J

b) Trabalho como variação de energia potencial gravitacional – W_XY=E_pX – E_pY=0 –m.g.h= – 0,2.10.0,1  —  W_XY= – 0,2J

c) Essa velocidade mínima ocorre quando o carrinho passa por Z estando em contato com a pista, mas sem pressioná-la, ou seja, quando a força de compressão  for nula.

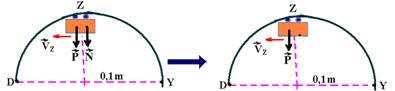
Nesse caso a força resultante centrípeta é o peso   —  F_RC=m.V_Z²/R  —  P= m.V_Z²/R  —  0,2.10=0,2.V_Z²/0,1  —  V_Z=1m/s

19-1- Correta. E_mA=mV_i²/2 + mgh=0 + mgh  —  E_mA=mgh  —  E_mC=E_cC + m.h.0  — E_mC=E_cC  —  sistema conservativo – E_mC=E_mA  —  E_mC=E_cC

2-Errada, pois se existem forças dissipativas, parte da energia mecânica é “perdida”

3- Correta. A força resultante centrípeta em B, já que a força de compressão aí é zero, é somente o peso P=mg  —  F_RC=mV_B²/R  —  mg= mV_B²/R  —  V_B=ÖRg e esse é o valor mínimo de V_B e para  qualquer valor acima dele,  sempre haverá força de compressão.

4- Errado. V_B é constante e vale ÖRg, mas V_C é fornecida por E_mA=E_mC  —  mgh=mV_c²/2  — V_c=Ö2gh (depende de h)

20- E_mD=mV²/2=m.20²/2  —  E_mD=200m  —  E_mA=m.g.H=m.10.H  —  E_mD=E­_mA  —  200m=10.m.H  —  H=20m  —  E_mC=m.10²/2 + m.g.h=m.100/2 + m.g.h  —  E_mC=50m + m.10.h  —  E_mD=E_mC  —  200m=50m + m.10.h  —  h=150/10  —  h=15m  R- E

21– a) Sistema conservativo – E_mP=E_mQ  —  mgh=mv²/2  — 10.20=V²/2  — V_Q=20m/s

b) Como não existe atrito, o sistema chega em R com velocidade de 20m/s (V_o=20m/s) e pára (V=0) após percorrer DS=1,5m  — 

Torricelli  —  V²=V_o² + 2.a.DS  —  0² = 20² + 2.a.1,5  —  a= – 400/3m/s²  —  F_m=m.a=90.(-400/3)  —  F_m=- 12.000N em módulo 

F_m=12.000N ou F_m=12kN

22- Antes do salto só tem energia cinética (com o nível zero de altura no ponto 0,8m)  — E_ma=m.V²/2   — na altura máxima só tem energia potencial gravitacional  — E_mam=m.g.h=m.10.3,2=32m  —  como não há dissipação de energia  —  m.V²/2=32m  —

V=8m/s R- D

23- Na situação inicial só tem energia potencial gravitacional  —  E_mi=m.g.4R  —  em x –E_mx=m.V_x²/2 + m.g.2R  —  4mgR= m.V_x²/2 + m.g.2R  — 2mgR=mV_x²/2  —  V_x=Ö4gR  —   V_x=2ÖgR 

No ponto x, agem sobre a esfera duas forças verticais e para baixo que são o peso P e a reação do trilho f_n  —  força resultante centrípeta – F_RC=mV_x²/R  —  P + f_n= mV_x²/R  —  mg +f_n=m(2ÖRg)²/R  —  f_n=m.4Rg/R – mg  —  f_n=3mg 

24- a) Vamos supor que seja no ponto X que a formiga perca contato com a bola. Nesse ponto, a reação normal  deixa de existir agindo sobre a formiga somente seu peso , que é a força resultante centrípeta, dirigida para o centro da circunferência e de intensidade F_RC=m.V_X²/R.

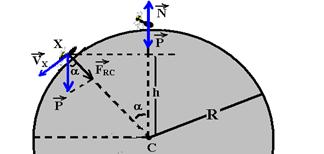
Observe no triângulo menor – cosa=F_RC/P  —  F_RC=P.cosa=mgcosa  —   mgcosa=mV_X²/R —  gcosa=V_X²/R I  —  observe no triângulo maior – cosa=h/R, que substituído em I  —  g.h/R=V_X²/R  —  V_X²=g.h   

b) Chamando a posição inicial da formiga de Y e considerando a horizontal que passa por X como nível zero de altura:

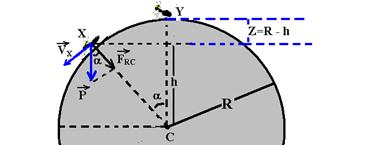
E_mY=E_cY + E_pY=0 + mg.(R-h)  —  E_mY=m.g.(R-h)  —  E_mX=E_cX + E_pX=m.V_X²/2 + 0  —  E_mX=m.V_X²/2  —  E_mY=E_mX  — 

m.g.(R-h)=m.V_X²/2  —  V_X²=2.g.(R-h)  —  que substituído em V_X²=g.h  —  g.h=2.g.R – 2.g.h  —  3h=2R  —  h=2R/3 

25– No instante em que o bloco deixa de estar em contato com os trilhos no ponto A, a força de compressão aí torna-se nula (N=0) e a força resultante centrípeta (F_RC) que atua sobre o bloco é seu peso P  —  F_RC=m.V_A²/2  — P=m.V_A²/2  —  m.g=m.V_A²/2  — 

V_A²=R.g   —  sem atrito (sistema conservativo) – E_mi=E_mA  —  m.g.h=m.g.R +  m.V_A²/2  —  g.h=g.R +g.R/2  —  h=R + R/2  — h=3R/2  R- C 

26– a) Em A só tem energia cinética – E_cA=m.V_A²/2=300.144/2  —  E_mA=21.600J  —  em C tem energia cinética e energia potencial  —  E_mC=m.V_C²/2 + m.g.h=300.V_C²/2 + 300.10.5,4=150.V_C² + 16.200  —  Em_A=E_mC  —  21.600=150.V_C²/2 + 16.200—  V_c=Ö36

—  V_C=6,0m/s  

b) No ponto C, a aceleração do carrinho é a aceleração centrípeta dada por a_C=V_C²/R=36/5,4  —  a_C=6.7m/s²

c) No ponto C, as forças que agem sobre o carrinho são seu peso para baixo e a reação dos trilhos para cima, cuja força resultante centrípeta vale  —  F_RC=P – N=m.V_C²/R  —  m.g –  Nm.V_C²/R  —  3000 – N=300.36/5,4  —  N=3.000 – 2.000  —  N=1.000N

27–a) Observe no gráfico que a energia potencial da bola varia com a altura sendo ambas função do tempo.

E_p(t)=m.g.H(t)  —  E_p(t)=0,6.10.H(t)  —   E_p(t)=6.H(t)  —  colocando valores para H, construímos o gráfico E_p X t:

t=0 – H=1,6m – E_p=6.1,6=9,6J  —  t=5 – H=0,6m – E_p=6.5=3J  —  t=t₁ – H=0 – E_p=0  —  t=9 – H=0,4 – E_p=6.0,4=2,4J e assim por diante.

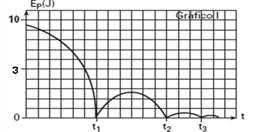
b) Como a energia total, que é a energia mecânica da bola se conserva no intervalo entre os choques, nesses intervalos E_t é constante e igual à energia potencial gravitacional nas alturas máximas, onde a energia cinética é nula (V=0).

 Nos pontos mais altos – E_m=E_t=E_p=constante

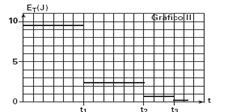
c) Para o choque que ocorre no instante t₁, a energia mecânica na altura máxima E_p1=E_m1=m.g.H_o=0,6.10.1,6  —  E_m1=9,6J é igual à energia cinética no choque com o solo  —  E_m1=E_c1=m.V₁²/2=0,6.V₁²/2  —  E_m1=0,3.V₁²  —  igualando, pois durante a queda a energia mecânica se conserva  —  9,6=0,3V₁²  —  V₁=Ö32  —  V₁=4Ö2m/s

Da mesma maneira, na segunda queda  —  E_m2=mgH=0,6.10.0,4=2,4J=m.V_R²/2=0,3V_R²  —  2,4=0,3V_R²  —  V_R=2Ö2m/s  —

Coeficiente de restituição  —  C_R=V_R/V₁=2Ö2/4Ö2  —  C_R=0,5

28- mgh=mV²/2  —  10.0,6=V²/2  —  V»3,46m/s  R-E

29– Energia mecânica na posição inicial  —  E_mi=E_ci + mgh=0,10 + 0,10.10.0,40=0,10 + 0,40  —  E_mi=0,50J  —  na altura h em que ela parar, E_c=0  —  E_mf=mgh=0,10.10.h=h  —  E_mi=E_mf  —  0,50=h  —  ele pára na altura 0,5m que está entre 1 e 2, fica oscilando até parar em 1  R- A

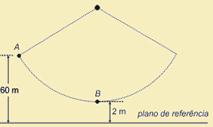
30- a) E_mA=mgh=60.10.4  —  E_mA=2.400J  —  E_mB =mV_B²/2 + m.g.h=60V_B²/2 + 60.10.0,8= 30V_B² + 480 —  2.400=30V_B² + 480  — 

V_B=8m/s

b) Trata-se de um lançamento obliquo com velocidade V_B, no ponto B. Nele, a velocidade de lançamento (inicial) V_B possui duas componentes V_Bx horizontal e constante durante todo o movimento e V_By, vertical e variável (lançamento vertical). No ponto mais alto da trajetória, ponto C, a componente vertical V_By se anula (V_By=0), restando apenas a componente constante

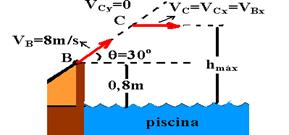
V_By=V_Bx=V_B.cosq=8.Ö 3/2  —  V_By=4Ö3m/s  —  E_Cy=m.V_By²/2=60.16.3/2  — E_Cy=1.440J              

c) E_mC= E_cC + E_Pc=60.(4Ö3)²/2 + 60.10.h_max  —  E_mA=E_mC  —  2.440=1.440 + 600h_max  —  h_max=1,6m

31- Energia mecânica inicial da mola (ponto P) – E_mi=E_Ci + E_Pei=0 + k.x²/2  —  E_mi= 10.x²/2  —  observe na figura abaixo que x=(2√2m), comprimento da mola deformada – (1m), comprimento natural da mola

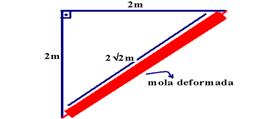
deformação inicial da mola – x=(2√2 – 1)m  —  E_mi=10.(2√2-1)²/2=5(2.1,4 – 1)²=5.1,8²—  E_mi=16,2J

Energia mecânica na situação final da mola (ponto T) – E_mf=E_Pef + E_Cf=kx_f²/2 + mV²/2  —  observe na figura abaixo que a deformação da mola na situação final é x_f=comprimento da mola deformada (2m) – comprimento natural da mola (1m)

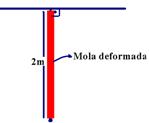
x_f=2 – 1=1m  —  E_mf=10.1²/2 + 1.V²/2=5 + V²/2  —  E_mf=5 + V²/2  —  16,2=5 + V²/2  —  V»√22,4 » 4,7m/s

32- Distensão máxima (10m) + comprimento natural (30m)=40m

Emi=Eci + Epi=0 +.750.40=30.000J  — situação final – distensão máxima – V=0+ – Ecf=0  —  Emf= 0 + kx2/2  —  Emf=50k —  30.00≈0=50k2  —  k≈24,5N/m

33- R – B veja teoria

34- R – A  veja teoria

35- E energia mecânica total (E) é só a energia cinética, pois o enunciado diz que a energia potencial não variou  —  o trabalho das forças dissipativas corresponde à energia total dissipada “perdida” no processo, no caso, entre 0 e 4s  —  W_fdiss=E(final) – E(inicial)=600 – 1800= – 1.200J –  em módulo 1.200J  R- B

36- E_mA=E_cA + E_pA=0 + m.g.h=2.10.3,5  —  E_mA=70J  —  E_mC=E_cC + E_pC=0 + 2.10.3  —  E_mC=60J  —  a energia dissipada corresponde ao trabalho realizado pelas forças dissipativas vale  —  W_fdis=DE_m=60 – 70= -10J – em módulo 10J – R A

37- Nas alturas máximas a energia cinética é nula e a mecânica é só a potencial gravitacional  —  DE_m=40.000J  —  DE_m=E_m1 – E_m2=mgh₁ – mgh₂₌10.10.(h₁ – h₂)  — DE_m=100.(h₁ – h₂)  —  40.000=100. Dh  —  Dh=400m R- C

38- A energia potencial gravitacional é a mesma em N e em P e como há perda de energia mecânica, a energia mecânica em N é maior que a energia mecânica em P. Assim, a energia cinética em N é maior que a energia cinética em P. Tendo perda de energia a E_mem P é maior que a E_m em Q  —  R- D

39- E_mA=E_pA + E­_cA=mgh + 0=4.10.8=320J  —  E_mC=E_cC + E_pC=mV²/2 + 0=4.100/2=200J  —  regra de três  —  320J – 100%  —  120J – x  —  x=37,5%  R- C

40- E_mi=kx²/2=100.0,001/2=0,5J  —  E_mf=mgh=0,1.10.0,3=0,3J  —  DE_m=W=0,3 – 0,5=0,2J  R- E

41- a) E_ci=mv²/2=2.1²/2  —  E_ci=1J

b) A energia mecânica inicial do bloco de massa 5kg é igual a 0,8J, pois houve perda de 20%.e toda essa energia é transmitida ao bloco quando se encontra no ponto A, tomado como nível zero de altura.

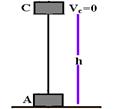
E_mA=0,8J  —  E_mC=mgh=5.10h  —  E_mC=50h  —  E_mA=E_mC  —  0,8=50h  —  h=0,16m

42-E_mA=mgh=25.10.2,4=600J  —  E_mB =mV²/2=25V²/2=12,5V²  —  F_at=mN=mPcos37=0,5.250.0,8=100N  —   sen37^o=h/d  —  d=4m  — W_fat=F_at.d.cos37^o=100.4.0.(-1)=-400J  —  W_fat=E_mB – E_mA  — -400=12,5V² – 600  — V=4m/s  R- D

43- a) Terra  —  E_mi=mgh=mgH_A  —  E_mx=mV_x²/2  —  como na rampa não existe atrito mgH_A = mV_x²/2  —  V_x²=2gH_A  — 

     Marte  —  E_mi=mg/3h=mg/3H_A  —  E_mx=mV_x²/2  —  como na rampa não existe atrito mg/3H_A = mV_x²/2  —  V_x²=2/3gH_A  — 

  V_xTerra²/ V_xMarte²=2gH_A/2/3gH_A  —    V_xTerra/ V_xMarte=Ö3

b)Terra  —  E_mx=E_cx=mV_x²/2  —  E_mx=m2gH_A/2=mgH_A  —  E_my=mV_y²/2=mV_y²/2  —  no trecho horizontal existe força de atrito  —  F_at=mN=mP=mmg  —  F_R=ma  —  F_R=F_at  —  ma=mmg  —  a=mg  —  Torricelli  —  V_y²=V_x² + 2(-a).DS  —  V_y²=2gH_A –   

2mgL  —  V_y²= 2g(H_A – mL)  —  W_fat=E_my – E_mx  — W_fat=mV_y²/2 – mV_x²/2  — W_fat=m2g(H_A – mL)/2 – m(2gH_A)/2   —  W_fat=

mg(H_A – mL) –  mgH_A  —  W_fatTerra= – mgmL                                                                                     

Marte  —  W_fatMarte= – mg/3mL  —  W_fatTerra/ W_fatMarte= – mgmL X – 3/mgmL  —   W_fatTerra/ W_fatMarte= 3

 

44- Calculando a energia mecânica na situação inicial i e na final f

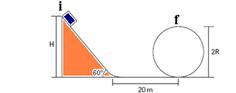
E_mi=mgH=mg20Ö3  —  E_mi=20Ö3mg I  —  E_mf=mg2R + mV_f²/2 – a condição para que ele faça o loop em f sem perder contato com a pista é V_f=ÖRg  —  E_mf=mg2R + m(Rg)/2  —  E_mf=2,5mRg II

Cálculo do trabalho das forças dissipativas (F_at):

 Trabalho do F_at  na rempa

 

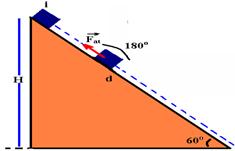
F^R_fat=mN=mPcos60⁰=mmgcos60^o=1/2.mg.1/2  —   F^R_fat=mg/4  —  sen60^o=H/d  — Ö3/2=20Ö3/d  —  d=40m  —  W^R_fat=F^R_fat.d.cos180^o=mg/4.40.(-1)  —  W^R_fat= – 10mg

Trabalho do F_at no plano horizontal:

F^PH_fat=mN=mP=mmg=1/2.mg  — F^PH_fat= mg/2  —  W^PH_fat = F^PH_fat.d.cos180^o=mg/2.20.(-1)  —  W^PH_fat= – 10mg

Trabalho total do F_at  —  W_fat= -10mg – 10mg  —  W_fat= – 20mg III

O trabalho das forças dissipativas (F_at) é igual à variação de energia mecânica  — W_fat=E_mf – E_mi  IV  —    substituindo I, II e III em IV  —  -20mg=2,5mgR – 20Ö3mg  —  R=(20Ö3 – 20)/2,5  —  R=8(Ö3 – 1)m 

R- C

45-

 

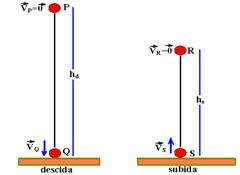
Descida  —  E_mP=mgh_d=1.10.2=20J  — —  E_mP=E_mQ  —  E_mQ=20J  —  subida  —  perde 12J, sobram 8J– E_mS =8J  —  E_mR=mgh₂=1.10.h₂=10h₂  —  E_mS = E_mR  —  10h₂=8  — h2=0,8m=80cm  R- D

 

46- a) Dados  —  m = 2 kg  —  h_o = 1 m  —   g = 10 m/s²  —  considere que a cada choque a bola perde 50% de sua energia mecânica, e que não haja perda de energia mecânica enquanto a bola está no ar  —  assim, após o primeiro choque, a energia cinética da bola E_c é 50% ou metade de sua energia potencial gravitacional inicial E_p  —  E_c=0,5E_p  —  E_c=mgh_o/2=2x10x1/2  — 

E_c=10J

b) Ao atingir o solo pela segunda vez, a bola tem a mesma energia cinética que tinha após o primeiro choque, calculada no item anterior  —  E_c=mV²/2  —  10=2V²/2  —  V=√10≈3,2m/s

c) Dado  —  E_c’=0,08J  —  após o n-ésimo choque, a energia cinética da bola é  —  E_c’=(1/2)ⁿ.mgh_o  —  0,08=(1/2)ⁿ.2x10x1  — 

(1/2)ⁿ=8/2000  —  (1/2)ⁿ=1/250  —  considerando 1/250≈1/256  —  (1/2)ⁿ=(1/256)  —  (1/2)ⁿ=(1/2)⁸  —  n=8

47- Nos dois casos, a deformação da mola é a mesma (x), armazenando as duas molas mesma energia potencial elástica  —  E_pel=kx²/2

  —  energia potencial gravitacional em relação à linha da mola não deformada  —  E_pg= = m g x  —  pela conservação da energia, a velocidade v_o de lançamento de um dardo é  —  E_c=E_pel + E_pg  —  mV_o²/2=mgx + kx²/2  —  V_o²=2/m(mgx + kx²/2)  —  V_o=√(mgx + kx²/2)  —  observe que, como a massa m aparece no denominador, o dardo de maior massa é o que tem menor velocidade inicial, ou seja, o dardo I, que tem um pedaço de chumbo grudado nele.

Após sair dos canos dos brinquedos, desprezando a resistência do ar, os dados ficam sujeitos exclusivamente à força peso, tendo, portanto, a mesma aceleração g  —  por isso os gráficos são retas paralelas, como mostrado na opção A  —  R- A

48- Observando a tabela dada  —  k=F_e/x=160/10=320/20=480/30  —  k=16N/cm=1.600N/m  —  k=1,6kN/m  —  R- B

49- A energia potencial elástica (Epot) armazenada no sistema é igual ao trabalho da força elástica W_fel para provocar essa deformação  —  como a força elástica varia com a deformação, esse trabalho é dado pela “área” entre a linha do gráfico e o eixo da deformação, como mostra a figura:

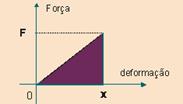
E_pot=W_fel=”área”=base x altura/2=x.F/2=x.(kx)/2  —  E_pot=kx²/2  —  R- A

50- Pela conservação da energia mecânica, a energia potencial elástica armazenada no sistema é transferida para a flecha na forma de energia cinética  —   dados relevantes  —   x = 1 m  —  m = 10 g = 10^-2 kg  —   k = 1.600 N/m  —  mV²/=kx²/2  —  v=x.√k/m  —V=1.√1.600/10^-2=√16.10⁴  —  v=400m/s  —  R- B

51- Como o sistema é conservativo, em todos os casos a velocidade em B é v_B, que pode ser calculada pelo Teorema da Energia Mecânica  —  fazendo AB = h  —  E_mA=E_mB  —  mgh=mV_B²/2  —  V_B=√2gh  —  sendo H a altura do solo até B, o tempo de queda (tq) é obtido pela expressão: H = gt_q²/2  —  t_q=√2H/g  —  na direção horizontal, o movimento é uniforme com velocidade v_B  —  a distância horizontal percorrida durante o tempo de queda é: d = v_B t_q  —  d =(√2gh).(√2H/g)  —  d=2√hH  —  sendo h e H iguais em todos os casos, a distância de B ao solo também é a mesma para todos eles. 

R- D

52- Como as forças dissipativas são desconsideradas, o sistema é conservativo e a energia mecânica é a mesma em todos os pontos  —    

R- A

53- Observe a figura abaixo que mostra os pontos de velocidade nula (A) e de velocidade máxima (B)  —  ela conservação da energia

mecânica  —  E_mA=E_mB  —  3mgh_A=3mhh_B + 3mV²/2  —  g(h_A – h_B)=V²/2  —  V²=20.(60 – 2)=1.160  —  V=√1.160  —  v ≈ 34 m/s  —  a energia cinética máxima a que eles ficam submetidos é a energia cinética do sistema formado pelos três jovens, no ponto de velocidade máxima (B)  —  E_c=3mV²/2=3x50x1.160/2  —  E_c=87.000J=87kJ

54- Observe que o sistema conservativo, a energia mecânica inicial, no lançamento, é igual à energia mecânica no ponto mais alto, que é o mesmo para as três trajetórias. Portanto, a energia potencial também é a mesma. Assim, fica na dependência da energia cinética. A partir do ponto mais alto, a trajetória de maior alcance horizontal é a III, portanto, a de maior velocidade horizontal e, consequentemente, a de maior energia cinética. Então, a trajetória III é a que apresenta maior energia mecânica no ponto mais alto, logo, maior energia mecânica no lançamento. 

R- C

55– A menor altura h é aquela que faz com que o carrinho passe pela posição (2) com a velocidade mínima permitida para um círculo vertical (quase perdendo o contato com a pista), ou seja, a força normal que a pista aplica no carrinho é praticamente nula  —  assim, a intensidade da força resultante centrípeta nessa posição (2) vale  —  F_c=N + P  —   F_c=0 + P  —  F_c= P  —  F_cé o próprio peso do carrinho  —  F_c=mV²/R  —  P=mg  —  mV²/R=mg  —  V²=Rg (I)  —  pela conservação da energia mecânica entre as posições (1) e (2)  —  E_p1=E_c2 + E_p2  —  mgh=mV²/2 + mg(2R)  —  2gh=V² + 4Rg (II)  —  substituindo (I) em (II)  —  2gh=Rg + 4Rg  —  h=5R/2  —  h=2,5.(24)  —  h=60m  —  R- C

56- Como o sistema é conservativo a energia mecânica total é constante e diferente de zero (gráfico III). Se a energia total é constante quando a energia potencial diminui a cinética deve aumentar ou quando Ep = máxima ® Ec =0 (gráfico I).  

R- B

57- Dados  —   h = 2,4 m  —   v_AB = 4 m/s  —  conservação da energia mecânica em AB e CD  —  E_mAB=E_mCD  —  mv²_AB/2 +

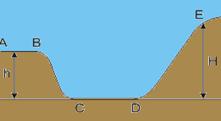
mgh=mv²_CD/2  —  4²/2 + 10×2,4=v²_CD/2  —  v²_CD=64  —  v_CD=8m/s  — conservação da energia mecânica em CD e E  —  E_mCD=E_mE  —  mv²_CD/2=mgH  —  8²/2=10H  —  H=3,2m  —  R- E

58- a) Dados: r = 80 cm = 0,8 m; h = 2 m; m = 36 kg; H = 6 m e g = 10 m/s²  —  como na descida o atrito é desprezível, o sistema pode ser considerado conservativo  —  então, tomando como referência o plano que contém o final do toboágua, pela conservação da energia mecânica  —  E_mi=E_mf  —  m g H = m g h + mV²/2  —  10 (6) = 10 (2) + V²/2  —   v² = 80  —  a força horizontal (F_x) sobre a criança durante a descida é a resultante centrípeta.

F_x = F_c = mV²/R= 36×80/08  —  F_x = 3.600 N.

b) Dados: v_o = 10,9 m/s; v = 0; DS = 1,5 m; g = 10 m/s²  —  durante a descida da criança na água da piscina, ela sofre a ação do peso () e das forças dissipativas exercidas pela água , em sentido oposto ao movimento, formando com a velocidade ângulo a = 180°. Aplicando o teorema da energia cinética  —  W_FR=ΔE_c  —  W_p + W_FDM=mV²/2  mV_o²/2  —  mgΔS + F_DMΔScos180^o=0 – mV_o²/2  —  10x36x1,5 – F_DMx1,5= -36x(10,9)²/2  —  1,5F_DM=540 + 2.138,6  —  F_DM=1.785,7J

59- a) No trajeto do ponto P até o ponto B, agem no bloco três forças: o peso  a normal  e a de atrito   —  a força peso realiza trabalho apenas ao longo da descida PA, a normal não realiza trabalho, pois é perpendicular à trajetória em todo o percurso, e a força de atrito somente realiza trabalho no trecho AB  —  aplicando, então, o teorema da energia cinética, notando que a energia cinética final em B é nula e que em P é 1/20 da energia potencial nesse mesmo ponto, suposta calculada a partir do plano horizontal de lançamento  —  W_R=ΔE_c  —  W_p(PA) + W_N(PB) + W_fat(AB) =E_cB  – E_cP  —  mg(H – h) + 0 – Fd= 0 – 1/20(mgH)  — 

mg(H – 0,15H) – μmg3H=-0,05mgH  —  μ=0,9/3  —  μ=0,3

b) ΔE_m=│W_fat│/E_mP=μmgd/1/20(mgH) + mgH  —  ΔE_m=0,3mg3H/21/20mgH  —  ΔE_m=18/21=0,857  —  ΔE_m(%)=85,7%

60- Dados: v = 10 m/s; g = 10 m/s²; h = 10 m; m = 2 kg  —  enquanto voa, no esquilo agem duas forças: o peso  e a força de sustentação  do ar. Como a velocidade é constante, o trabalho da resultante  é nulo. Mas o trabalho da resultante é igual ao somatório dos trabalhos das forças atuantes  —    —      —   m g h =  —   – 2 (10) (10)  — 

W_fat= 200 J  —  R- B

61- Pelo teorema da energia cinética, o trabalho da resultante W_R das forças que atuam sobre um corpo é igual à variação da energia cinética do corpo  —  como a velocidade é constante, esse trabalho é nulo.     —  R- A

62- A energia total do corpo na altura  de 10m vale E_m=mgh=2.10.10  —  E_m=200J  —  ao chegar ao solo  a energia cinética vale E_m=200 – 4  —  E_m= 196J  —  E_m=mV²/2  —  196=2V²/2  —  V=√196  —  V=14m/s  —  R- B

63- a) Velocidade de A imediatamente antes de se chocar com B  —  conservação da energia mecânica  —  mgh=mV²/2  —  10.0,8=V²/2  —  V=4m/s  —  velocidade de B imediatamente após o choque com A  —  Q_i=Q_f  —  m_AV_i=m_BV_f  —  3.4=3.V_f  — 

V_f=4m/s

b) Como, no o atrito é desprezível o bloco B incide na mola com velocidade de 4m/s e a mola é comprimida de x, até o bloco B parar (V=0)  —  conservação da energia mecânica  —  imediatamente antes de se chocar com a mola o bloco só possui energia cinética E_mi=mV²/2=3.16/2=24J  —  quando o bloco B pára ele só possui energia potencial elástica armazenada  —  E_mf=kx²/2=4x²/2  —  E_mf=2x²  —    E_mi=E_mf  —  24=2x²  —  x=√12  —  x≈3,46m

c) Agora, com atrito no plano horizontal a única força na direção do movimento é a força de atrito  —  F_at=μN=μP=0,4.30  — 

F_at=F_R=ma  —  12=3.a  —  a=4m/s²  —  como a velocidade do bloco B está diminuindo essa aceleração é negativa  —  equação de Torricelli até o bloco B parar  —  V²=V_o² + 2.a.ΔS  —  0=4² + 2.(-4).ΔS  —  ΔS=2m  —  como d=3m, o bloco B não comprime a mola parando a 1m da mesma.

 

64-

 

65-

  a) Quando o bloco da esquerda de massa m_e=2,0kg chega à superfície rugosa com velocidade de V_o=1m/s, a força de atrito, contrária ao movimento, que é a força resultante sobre ele, faz com que surja uma aceleração de retardamento até que ele pare

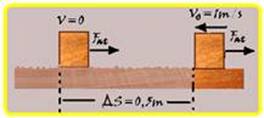
(V=0) após percorrer a distância ∆S=0,5m  —  cálculo da aceleração de retardamento  —  Torricelli  —  V²=V_o² +2.(-a).∆S  —  0² = 1²-2.a.0,5  —  a=1m/s²  —  na direção do movimento a força resultante sobre o bloco é a força de atrito F_at  —  2^a lei de Newton  —  F_R=m.a=F_at  —  F_at=2.1=2N  —  F_at=μN=μP=μmg  —  2=μ.2.10  —  μ=0,1.

b) Utilizando o teorema da conservação da quantidade de movimento  —  Q_antes=m₁V₁=m₂V₂=m₁.0 + m₂.0=0  —  Q_depois=m₁.V₁ +

m₂.V₂ = 2.(-1) + 1.V₂=V₂ – 2  —  Q_antes = Q_depois  —  0=V₂ – 2  —  V₂=2m/s.

c) Utilizando o teorema da conservação da energia mecânica, enquanto a mola está comprimida a energia total (mecânica) armazenada é a energia potencial elástica que vale  —  E_Mantes=E_pe=kx²/2  —  depois que a mola é liberada e cada bloco se move

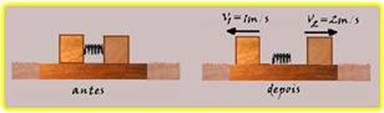
em sentidos contrários com velocidades V₁=1m/s e V₂=2m/s, toda energia potencial elástica sedo sistema se transforma em energia cinética  —  E_Mdepois=m₁.V₁²/2 + m₂.V₂²/2=2.(-1)²/2 + 1.2²/2=3J  —  E_Mantes = E_Mdepois  —  kx²/2=3  —  6.10⁴.x²/2 = 3  —  x² = 10^-4  — x=10^-2m=1,0cm.

66-

  Pela conservação da quantidade de movimento  —  Q_antes=m.V + 2m.0  —  Q_antes=m.V  —  Q_depois=(m + 2m).V’  —  Q_antes

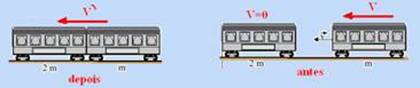
=Q_depois  — m.V=3m.V’  —  V’=V/3  —  supondo que a energia mecânica do sistema de massa 3m se conserve, como a altura não

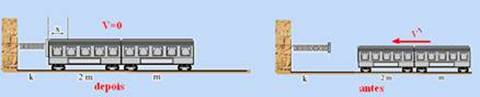
varia, toda energia energia cinética antes do contato com a mola se transforma em energia potencial elástica após a composição parar e a mola for comprimida de x  —  E_c=3mV’²/2 —  E_pe=kx²/2  —  E_c=E_pe  —  3mV’²/2 = kx²/2  —  (3m/2)/(V/3)² = kx²/2  —  x = v ·√ m/ (3k)  —  R- E

 

67-

 Como as forças externas são desprezadas, o sistema é conservativo e a energia mecânica é constante sendo a soma da energia cinética com a potencial gravitacional:

a) Falsa  —  a energia mecânica é constante.

b) Falsa  —  quanto maior o afastamento, maior será altura atingida (ponto B) e, consequentemente maior a energia potencial e claro, também a mecânica.

c) Correta

d) Falsa  —  a energia mecânica máxima total do sistema depende apenas da altura máxima atingida pelo ponto B.

e) Falsa  —  em B, onde V=0 a energia cinética (E_c=mV²/2) é nula e a energia potencial gravitacional (E_p=mgh) é máxima.

R – C          

  

 68-

Cálculo da altura h  —  sen30^o=h/1440  —  h=720m  —  não havendo atrito o sistema pode ser considerado conservativo  —

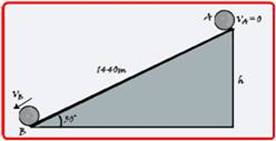
teorema da conservação da energia mecânica  —  E_mA=mV_A²/2 + m.g.h = 0 + m.10.720  —  E_mA=7.200m  —  E_mB=mV_B²/2 + m.g.h = E_mB=mV_B²/2 + 0  —  E_mB=mV_B²/2  —  E_mB=E_mA  —  mV_B²/2 = 7200m  —  V_B²=14400  — V_B=120m/s  —  R- B

 

69-

Entre A e B não tem atrito e a força na direção do movimento é a força resultante  (veja figura)  —  cálculo da

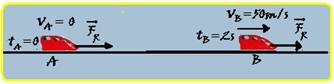
aceleração do movimento  —  V_B=V_A + a.t  —  50 = 0 + a.2  —  a= 25m/s²  —  intensidade da força resultante  —  princípio fundamental da dinâmica  —  F_R=m.a=800.25  —  F_R=20 000N  —  entre B e C (começo da subida da

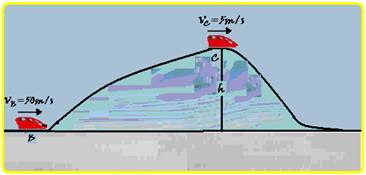
rampa), houve energia perdida devido aos atritos de valor E_P=190 000J  —  energia mecânica em B  —  E_mB=mV_B²/2 +

m.g.h=800.50²/2 + 800.10.0  —  E_mB=1 000 000J  —  energia mecânica em C  —  E_mC=mV_C²/2 + m.g.h=800.5²/2 +

800.10.h  —  E_mC=10 000 + 8 000h  —  observe que E_mA = E_P + E_mC  —  1 000 000 = 190 000 + 10 000 + 8 000h  — 

8 000h = 800 000  —  h=100m  —  R- C.

 

70-

Como não existem forças dissipativas a energia mecânica é constante  —  no ponto fornecido  —  E_mA=E_cA + E_pA  —  E_mA=9 + 9=18J  —  quando chega ao solo h=0 e sua energia potencial gravitacional é nula  —  no solo  —  E_ms=mV²/2 + mgh=4.V²/2 + 4.10.0  —  E_ms=2V²  —  E_mA = E_ms  —  18=2V²  —  V=3m/s  —  R- C.

 

71-

Como o sistema é conservativo toda energia mecânica é sempre a mesma em qualquer instante  —  imediatamente antes do salto ele deve ter a maior velocidade possível (EtapaI) e consequentemente maior energia cinética (Ec=m.V2/2)  —  essa maior energia cinética, deve se transformar em energia potencial elástica (Etapa II) que acontece quando a vara é deformada  —  então, essa máxima energia potencial elástica é transformada em energia potencial gravitacional (Ep=m.g.h) para que a maior altura atingida (Etapa III) também seja máxima  —  R- C.

 

Voltar para os Exercícios