Conservação da Quantidade de Movimento – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Conservação da Quantidade de Movimento

 

 01- R- C  (veja teoria)

02- Q_a=mV=(250 ).10  —  Q_a=2.500kg.m/s  —  Q_d=m_c.V_c + m_t.V_t=50.(-10) + 200.(+V_t)  —  Q_d= – 500 + 200.V_t  —  Q_a=Q_d  —  2.500= – 500 +200.V_t  —  V_t=15m/s R- E

03- (01) verdadeira (veja teoria)  —  (02) falsa – sua massa é diferente da massa do tanque  —  (04) verdadeira –  (ambos estavam parados)  —  (08) falsa – ambos possuem velocidades de sentidos contrários  —  (16) antes do choque do tanque com o astronauta B – Q_a=m_t.V_t + m_B.V_B  —  10.5 + 90X0  —  Q_a=50kg.m/s  —  após o choque, astronauta + tanque (m=90 + 10=100kg) tem velocidade comum V  —  Q_d=100.V  —  Q_a=Q_d  —  50=100V  —  V=0,5m/s(verdadeira)

(01+04+08+16)=29

04- antes  —   Q_a=m_a.V_a + m_SH.V_SH =10.000X100 + 50.(-V_SH)  —  Q_a=10⁶ – 50V_HS  —  depois  —  Q_d=m_SH.V_SH + m_a.V_a=0 + 0=0  —  Q_a=Q_d  —  100.10⁴ – 50.V_SH  —  V_SH=2.10⁴km/h R- A

05- Sendo a velocidade uma grandeza vetorial, vamos orientá-la como, por exemplo, para a direita positiva e para a esquerda, negativa e vamos supor que, após o choque, ambos os fragmentos se movam para a direita  —  Q_a (antes da explosão)  —  Q_a=mV=m.10  — Q_a=10m  —  Q_d (depois da explosão)  —  Q_d=m/2V₂ + m/2V₁  — Q_d=(mV₂ + mV₁)/2  —  Q_a = Q_d  —  10m=(mV₂ + mV₁)/2  —  V₂+ V₁=20  —  com a trajetória orientada para a direita, a soma algébrica das duas velocidades deve ser 20.(01) +15 -5=10m/s (falsa)  —  (02) +20 + 0=20m/s (verdadeira)  —  (04) +30 -10=20m/s (verdadeira)  —  (08) +25 + 0=25m/s (falsa)  —  (16) +25 – 5=20m/s (verdadeira)  —  (32) +10 + 0=10m/s (falsa)  —  (64) +50 – 30=20m/s (verdadeira)  

Soma (02 + 04 + 16 + 64) = 86

06- Q_a=0  —  Q_d= mv +M(-V)=60.∆s/∆t – 80.∆S/∆t= 60.∆s/∆t – 80.12/∆t   —  Q_d=  60.∆s/∆t – 960/∆t   —  Q_a=Q_d  —  0=60.∆s/∆t – 960/∆t  —  ∆t é o mesmo e se cancela   —  60.∆s=960  —  ∆s=16m  —  a distância entre eles é d=12m + 16m  —  d=28m

07- Q_a=0  —  Q_d=(45 + 1).(-V_s) + (m + 1).V_i= – 46V­_s + (m + 1)V_i= – 46.10/∆t + (m + 1).30/∆t  —  Q_d=( – 460 +

 

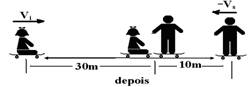
30m + 30)/ ∆t  —Q_a=Q_d  —  0==( – 460 + 30m + 30)/ ∆t  —  30m – 430=0  —  m=14,33kg R- D

08- a) Q_a=0  —  Q_d=M₁.V₁ + M₂.V₂=234.10^-3.1,0.10² + 4.10^-3.V₂  —  Q_d=234.10^-1 – 4.10^-3.V₂  —  Q_a=Q_d  —  0=234.10^-1 – 4.10^-3.V₂  —  V₂=5,85.10³m/s

b) a variação da energia cinética da partícula fornece o trabalho necessário para pará-la  —  E_ca=0  —  E_cd=234.10^-3(1,0.10²)²/2 +4.10^-3.(5,85.10³)²/2  — W=E_cd – E_ca= – 6,8.10⁴J   

c) W=F.d.cos0^o  —  6,8.10⁴=F.10  —  F=6,8.10³N

09– a) cálculo da componente vertical (V_oy) da velocidade inicial V_o  —  na altura máxima (h=45m) – V_y=0  —  V­y² = V_oy² + 2.(-g).h  —  0²=V_oy² – 2.10.45  —  V_oy=30m/s  —  tempo para atingir a altura máxima  —  V_y=V_oy –gt  —  0=30 – 10.t  —  t=T_o=3s

b) para atingir a altura máxima ele percorreu uma distância horizontal x=60m em t=3s  —  x=x_o + V_x.t  —  60=0 + V_x.3  —  V_x=20m/s

c) no ponto mais alto da trajetória o rojão, antes de explodir, tem apenas velocidade horizontal V_x=20m/s e sua quantidade de movimento vale Q_a=mV=0,5.20  —  Q_a=10kg.m/s (horizontal e para a direita)  —  após a explosão, as componentes horizontal e vertical do fragmento A são nulas, sobrando apenas a componente horizontal do fragmento B, que também deve ser horizontal e para a direita, pois, Q_a=Q_d  —  Q_d=0,25.V  —  10=0,25.V  —  V=40m/s (componente horizontal da velocidade do fragmento B)  —  a energia fornecida pelo combustível corresponde à variação de energia cinética antes e depois da explosão, tomando este ponto como nível zero de altura (E_p=0)   —  E_ca=mV²/2 =0,5.400/2   —  E_ca=100J —  E_cd=0,25.1600/2=200J  —  DE_c=200 – 100=100J

10- Sendo a massa do maior o dobro da massa do menor, a velocidade do menor (V₁) deverá ser o dobro da velocidade do maior (V₂), pelo princípio da conservação da quantidade de movimento  —  V₁=2V₂)  —  ∆S₁/∆t=2∆S₂/∆t  —  sendo ∆t o mesmo  — ∆S₁=2∆S₂  —  ∆S₁/∆S₂=2 R- C

11- O pescador deve correr para B, a fim de que a força que seus pés exercem sobre a jangada a

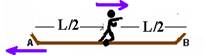
acelere no sentido B para A, fazendo com que ela se afaste da trajetória do torpedo.

12- a) Pela 3.a lei de Newton, ou princípio fundamental da ação e reação o barco irá para trás.

b) F.∆t=m∆V  —  250.2=(180 + 70).(V – 0)  —  V=2,0m/s

13-(01) Falsa – massas diferentes, velocidades diferentes.

02-Verdadeira – verdadeira, pois a massa de A é o dobro da massa de B

(04) Falsa

(08) Correta – a quantidade de movimento do sistema antes de puxar a corda é igual à quantidade de movimento do sistema após o puxão.

(16) Falsa – vide teoria

Soma – (02 + 08) = 10

14- O sistema deverá conservar a quantidade de movimento horizontal inicial. Desta forma como a velocidade foi reduzida à metade, a massa do sistema deverá dobrar, passando de 30 g para 60 g. A diferença de 30 g corresponde a massa da bolinha de isopor.  R- D

15- a) W=F.d.cosa=25.4.cos0^o  —  W=100J

b) velocidade com que a poltrona chega em B  —  F=ma  —  25=10.a  —  a=2,5m/s²  —   V_B²=V_o² + 2.a.DS  —  V_B²=0² + 2.2,5.4  —  V_B=√20m/s  —  velocidade com que a poltrona chega à Maria (V_M) – conservação da energia mecânica – E_mB =m.V_B²/2 + mgh=10.(√20)²/2 + 10.10.0,8  —  E_{mB =}180J  —   E_mM=m.V_M²/2 + m.g.h=10.V_M²/2 + 0  —  E_mM=5V_M²  —  180=5V_M²  —  V_M=6m/s

c) conservação da quantidade de movimento – antes de Maria sentar na poltrona – Q_a=m.V=10.6  —  Q_A=60kg.m/s  —  depois que Maria sentou, o sistema Maria + poltrona movem-se juntos com velocidade V  —  Q_d=60.V  —  Q_a=Q_d  —  60=60V  —  V=1m/s

16- Q_a=50.(+2) + 10.(-2)=80kg.m/s  —  Q_d=50.(V) + 10.(-0,5)=50V – 5  —  Q_a=Q_d  —  80=50V – 5  —  V=1,7m/s R- D

17- R- A (veja teoria)

18- Velocidade de recuo do rifle  —  Q_a=0  —  Q_d=15.10^-3.(+3.10²) + 5.(-V)  —  Q_d=45.10^-1 – 5V  —  Q_a=Q_d  —  0=45.10^-1 – 5V —  V=0,9m/s  —  velocidade de recuo do atirador  —  Q_a=0  —  Q_d=15.10^-3.(+3.10²) + (95 +5).(-V)=45.10^-1 – 100V  —  Q_a=Q_d  —  0=45.10^-1/100V  —  V=4,5.10^-2m/s

19- a) Q_a=M_c.V_c=10.5=50kg.m/s  —  Q_d=(90 + 10).V=100V  —  Q_d=Q_a  —  50=100V  —  V=0,5m/s

b) E_ca=10.25/2=125J  —  E_cd=100.0,25/2=12,5J  —  ∆E_c=E_cd – E_ca= 12,5 – 125  —  ∆E_c=-125J

20-(1) Verdadeira – desprezando-se os atritos ele está em queda livre sob ação exclusiva da força peso.

(2) Velocidade com que ele chega ao solo – V²=V_o² + 2g.h  —  V²= 0² + 2.10.0,5  —  V=√10m/s  —  módulo da aceleração durante o choque  —  V²=V_o² + 2.a. DS  —  0²=(√10)² -2.a.0,03  —  a=333m/s²  —  F=ma=70.333,3  —  F=23.310N (força que ele troca com o solo) que é maior que o peso de 1.000kg (1.000 X 10=10.000N) – Verdadeira

(3) Verdadeira – princípio da ação e reação

(04) Verdadeira – (veja teoria).

Todas verdadeiras 

21- a) Objeto A – queda livre com V_oA=0  —  a colisão ocorre na altura de h=(45 – 25)=20m  —  V²=Vo² + 2.g.h  —  V²= 0² + 2.10.20  —  V=20m/s  —  No encontro V_A=V_B=20m/s – antes da colisão Q_a=M(+V_A) + M.(-V_B)=M.(+20) + M.(-20)  —  Q_a=0  —  Q_d=2M.V_AB  —  Q_a=Q_d —  2M.V_A=0  —  V_AB=0  —  a energia mecânica dissipada na colisão corresponde a E_mdepois – E_mantes  —  DE_m=2M.V_AB – (M.V_A²/2 + M.V_B²/2)= 2.4.0 –(4.20²/2  + 4.(-20)²/2)  —  —  DE_m= 0 –(800 + 800)  —  DE_m= – 1600J  

b) variação de energia mecânica  —  E_mA= E_pA­ + E_cA = mgh + 0= 8.10.25  —  E_mA=2.000J  —  E_md=E_cd + E_pd=E_cB + 0  — E_mA=E_{md  —}  E_cB=2.000J

22-Orientando a trajetória como positiva no sentido do movimento da sonda (positivo para a esquerda)  —  antes – bola chegando à sonda  com velocidade de 2.000m/s e a sonda inicialmente parada  —  Q_a=m_b.V_b + m_s.V_s=10.2.000 + 1.000 X 0  —  Q_a=20.000kg.m/s  —  depois – bola saindo com velocidade V_b=- 400m/s e a sonda se movendo para a esquerda com velocidade +V  —  Q_d=m_b.V_b + m_s.(+V)=10.( – 400) + 1.000V  —  Q_d= – 4.000 + 1.000V  —  Q_a=Q_d  —  20.000= – 4.000 + 1.000V  — 

V=24m/s 

23- Como a direção e o sentido da velocidade coincidem com a direção e sentido da quantidade de movimento, e como a quantidade de movimento do sistema antes da explosão é nula, depois da explosão também deverá ser nula. Assim, a única alternativa em que todos os vetores se anulam é a D.

24- Q₁=m₁.V₁  —  Q₂=m₂.V₂  —  m₁=m₂ e V₁=V₂  —  Q₁=Q₂=Q, que somados vetorialmente fornecem  Q₁₂

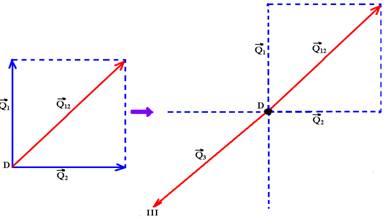
Como a quantidade de movimento antes da explosão é nula, a mesma, depois da explosão também deverá ser nula, o que só poderá ocorrer se   anular    R- III

25- Multiplicando as velocidades pelas respectivas massas obtemos as quantidades de movimento de cada elemento do sistema antes e depois da fissão

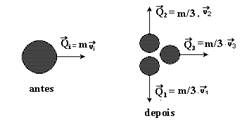
Observe na figura acima que  e  se anulam, sobrando:

Em módulo  —  Q_a=Q_d  —  Q_i=Q₃  —  m.v_i=m/3.v₃  —  v_i=v/3  R- E

26- Sendo a quantidade de movimento da granada antes da explosão vertical e para cima, sua quantidade de movimento depois da explosão também deverá ser vertical e para cima e na horizontal deve se anular. R- A

27- Cálculo do módulo de Q₁ e de Q₂ imediatamente depois da explosão  —   Q₁=m₁.V₁= 20.20=400kg.m/s  —  Q₁= Q₂=400kg.m/s  —  somando vetorialmente  e  obtemos  cujo 

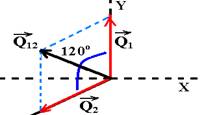
módulo é calculado pela lei dos cossenos  —  Q₁₂² = Q₁² + Q₂² + 2Q₁Q₂cos120^o  —  Q₁₂²= 400²  + 400² + 2.400.400.(-1/2)  —  Q₁₂=400kg.m/s  —  como a quantidade de movimento antes da explosão é Q_a=0, a quantidade de movimento depois da explosão será também nula (Q_d=0) e, para que isso ocorra  deve anular  , ou seja, deve ter a mesma intensidade, mesma direção e sentido contrário (figura abaixo

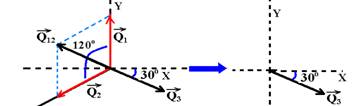
R- D

28- a) Quantidade de movimento do núcleo de trítio antes de se desintegrar  —  Q_a=0 (repouso)  —  após a desintegração – núcleo do hélio – Q_He³=12.10^-24kg.m/s  —  eletron – Q_e^– =6,0.10^-24kg.m/s  

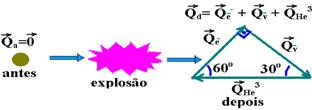
Sen60^o= Q_v / Q_He³  —  √3/2=Q_v/12.10^-24  —  Q_v=6,0.√3.10^-24kg.m/s

b) Q_He³=m.V  —  12.10^-24=5,0.10^-27.V  —  V=2,4.10³m/s

29-  Antes  —  Q_a=m.v_o 

Depois – Q_o=m/3.3v_o=m.v_o – Q₁=m/6.v₁ – Q₂=m/2.v₂

a) Como a quantidade de movimento () antes da explosão é horizontal e para a direita, a quantidade de movimento de movimento () depois da explosão também deverá ser horizontal e para a direita. Assim,  e  devem se anular, ou seja  — 

Q_o=Q₂  —  m.v_o=m/2.v₂  —  v₂=2.v_o

b) Como os vetores verticais se anulam,  deve ser igual a , ou seja,  —  m.v_o=m/6.v₁  —  v₁=6.v_o   

c) Considerando a energia mecânica como sendo apenas a cinética  —  antes –E_ma=m.v_o²/2  — depois  —  E_md=m/3.(3v_o)²/2 + m/6.(6v_o)²/2 + m/2.(2v_o)²/2  — E_md=11m.v_o²/2  —  E_md>E_ma – aumenta

30- a) eixo X  —  antes  —  Q_a=m.V=6.V  —  depois  —  Q_d=Q_AX + Q_BX  —  Q_d=m_A.V_A+ m_B.V_B  —  Q_d=m_A.V/2 + m_B.2V

Q_a=Q_d  —  6.V=m_A.V/2 + m_B.2V  —  12=m_A + 4m_B  I  —  m_A + m_B=6  —  m_A=6 – m_B  II  —  II em I  —  12=6 – m_B + 4m_B  — 

m_B=2kg  —  m_A=4kg

b) na vertical a resultante é nula  —  Q_AY=m_A.V_Y=2.V_A  —  Q_BY=m_B.V_Y=4.V_B

 

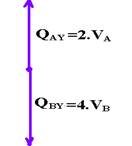
Q_AY=Q_{BY  —}  2V_A=4V_B  —  V_A/V_B=2

31- a) Dados  —  m_a = 60 kg  —   m_p = 80 kg  —   v_a = 0,15 m/s  —  como se trata de um sistema isolado, há conservação do momento linear (quantidade de movimento) do sistema (Q)  —  Q_i=Q_f  —  Q_i=0 (inicialmente em repouso)  —  Q_f=m_aV_a + m_pV_p  —  Q_i=Q_f  —  0= m_aV_a + m_pV_p  —  60.V_a=80.(0,15)  —  V_a= -0,2m/s  (sinal negativo significa que o astronauta recuou)  — V=0,2m/s

|b) Após o empurrão, o momento linear do painel é  —  Q_p = m_p v_p  = 80.(0,15) = 12 kg.m/s  —  como a força aplicada pelo astronauta é a responsável pela variação da velocidade do painel, temos, pelo teorema do impulso  —  I_Fa=Q_p=12kg.m/s  —

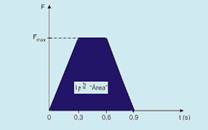
O impulso é numericamente igual à área  —  I_Fa=área do trapézio=(B + b).h/2=(0,9 + 0,3).F_max/2  —  I_Fa=0,6F_max  —  12=0,6F_max  —  F_max=20N

32- 01) Correta  — trata-se de um sistema mecanicamente isolado (a resultante das forças externas é nula), portanto ocorre conservação da quantidade de movimento ou momento linear  —  como a quantidade de movimento inicial do sistema é nula, para ocorrer conservação, o módulo da quantidade de movimento adquirida pelo homem deve ser igual ao módulo da quantidade de movimento adquirida pelo menino  —  M_H v_H = M_m v_m  —  60.(0,3) = 30. v_m  —  v_m = 0,6 m/s  —  a velocidade relativa de afastamento entre eles tem módulo  —  v_rel = 0,6 + 0,3 = 0,9 m/s  —  então, 2 s após o empurrão, a distância (d) entre eles é:
d = v_rel.Δt = 0,9.(2)  —  d = 1,8 m.
02) Falsa  —  o sistema é não-conservativo, pois homem e menino consomem energia de seus organismos, trocando forças que realizam trabalho mecânico, transferindo energia cinética ao sistema.
04) Falsa. Forças conservativas transformam energia potencial em cinética ou vice-versa  —  no caso há transformação de energia química dos organismos em energia cinética.
08) Correta  —  as forças trocadas entre eles têm mesma intensidade, pois formam um par ação-reação  —  como são forças internas ao sistema, a resultante dessas forças é nula.

16) Falsa  —  veja (01)

32) Correta  —  apenas forças externas alteram a quantidade de movimento do sistema, conforme afirma o teorema do impulso  —   resultante das forças externas é igual à variação da quantidade de movimento do sistema. 

R- (01 + 08 + 32) = 41

33- Trata-se de um sistema mecanicamente isolado, pois apenas forças internas provocam variações de velocidades  —  assim, ocorre conservação da quantidade de movimento do sistema  —  como se trata de uma grandeza vetorial, as partículas  e devem ter velocidades de sentidos e de mesmo módulo, uma vez que as massas são iguais  —  essas velocidades também devem se anular, pois como a quantidade de movimento inicial é nula, a final também deverá ser nula  —  R- A

34- As variações de velocidades na colisão ocorrem somente pela interação entre a massa m₁ e a massa m₂ formando, então, um sistema mecanicamente isolado  —  assim, há conservação da quantidade de movimento do sistema que engloba m₁, m₂ e a mola  —  a compressão máxima da mola ocorre quando os dois corpos têm a mesma velocidade

35- a) Dados  —  h_o = 2 m  —   H = 20 m  — v_o = 21 m/s  —   massa da flecha = m  —   massa do alvo = 5 m  —  conservação da energia mecânica  —  cálculo da velocidade com que a flecha atinge o alvo  —  E_mi=E_mf  —  mV_o²/2 + mgh=mV²/2 + mgH  — 

multiplicando por 2 a equação   —  v² = 21² + 20(2 –20)  —   v²= 81  — v = 9 m/s  —  como a flecha atinge o alvo no ponto mais alto, no momento de impacto a velocidade do alvo é nula  —  o sistema pode ser considerado mecanicamente isolado, e a colisão é inelástica  —  assim, pela conservação da quantidade de movimento (momento linear), sendo v’ a velocidade final do sistema  —    —   mv = (m + 5m)v’  —   v = 6v’  —   9 = 6v’  —   v’ = 1,5 m/s.

b) Cálculo do tempo de queda (t_q) do sistema  —  H=gt_q²/2  —  t_q=√2×20/10  —  t_q=2s  —  na direção horizontal você tem um movimento uniforme  —  X=V’.t_q=1,5×2  —  X=3m

36- Dados  —   massa da mala – m_l = 20 kg  —   velocidade da mala – v_l = 4 m/s  —   massa do carrinho – m₂ = 60 kg  —   velocidade do carrinho – v₂ = 0  —   velocidade final do sistema (m₁ + m₂) – V  —  observe que o sistema é mecanicamente isolado apenas nadireção horizontal  —  assim, só há conservação da Quantidade de Movimento (ou Momento Linear) apenas nessa direção  —  Q_antes = Q_depois  —   m₁v₁ + m₂v₂ = (m₁ + m₂)V  —   20(4) + 60(0) = (20 + 60)V  —   80 = 80V  —   V = 1 m/s  —  quanto a Energia Mecânica, seria desnecessário cálculo, pois pode-se analisar esse caso como uma colisão inelástica (os corpos seguem juntos), onde há dissipação de Energia Mecânica (a Energia Mecânica só se conserva em choques perfeitamente elásticos)  — provando  —  como a altura não varia ocorre apenas variação de energia cinética  —   E_mi=m₁V₁²/2=20×4²/2  —  E_mi=160J  —  E_mf=(m₁ + m₂)V²/2 =80×1²/2=40J  —  a energia mecânica passou de 120J para 40J, ou seja, diminuiu  —  R- C

37- Dados  —  M_G = 300 g  —  M_M = 100 g  —  V_G = 80 km/h  —  V_M = 24 km/h  —  antes da caça, os módulos das quantidades de movimento do gavião e do melro são, respectivamente  —  Q_G = 300 (80) g.km/h=24.000gkm/h  —  Q_M = 100 (24) g. km/h  —Q_M=2.400gkm/h  —  como ocorre conservação da quantidade de movimento no momento da caça, o vetor velocidade  tem a

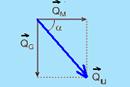
mesma direção da quantidade de movimento do sistema gavião-melro  —  observe na figura que tgα=cateto oposto/cateto adjacente  —  tgα=Q_G/Q_M=24.000/2.400  —  tgα=10  —  R- B

 

38-  a) Se você considerar o sistema carro-ônibus como um sistema isolado, você pode utilizar o teorema da conservação da

 quantidade de movimento  —  Q_antes=M.V_o + m_a.V_a=9000.80 +1000.0  —  Q_antes=720000kg.m/s  —  Q_depois=(M + m_a).V=10.000.V

Q_depois=10000V  —  Q_antes = Q_depois  —  720000=10000V  —  V=72km/h.

b) Pela figura fornecida você pode determinar a intensidade da força lateral   —  sen3^o=F_L/F_at  —  0,05=F_L/8000  —  F_L=400N  

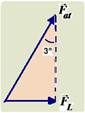
A aceleração lateral  do carro tem intensidade  —  F_L=m.a_L  —  400=1600.a_L  —  a_L=0,25m/s²

 

Voltar para os exercícios