Aplicações das Leis de Newton em blocos apoiados ou suspensos – Resolução

Resolução comentada dos exercícios de vestibulares sobre Aplicações das Leis de Newton em blocos apoiados ou suspensos

 

 

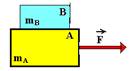
01– a) Como não existe atrito, por menor que seja a massa do sistema e a força aplicada o sistema sempre se moverá no caso, para a direita. Colocando as forças que agem sobre cada bloco apenas na direção do movimento (forças horizontais).

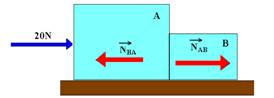
N_AB – intensidade da força que A aplica em B.          N_BA – intensidade da força com que B reage em A. Como N _AB e N_BA constituem par ação e reação elas tem a mesma intensidade que chamaremos de N.

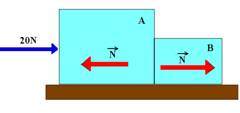
Bloco A  —  F_R=m_A.a  —  20 – N=3.a I              Bloco B  —  F_R=m_B.a  —  N=1.a II

Somando I com II, obtemos  —  20=4a  —  a=5m/s² (é a mesma para cada bloco, pois se movem juntos).

b) Substituindo a=5m/s² em I ou em II obtemos  —  N=5N.

c)

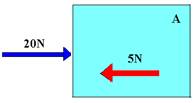
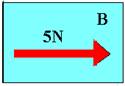
Observe nas figuras acima que F_RA=20 – 5=15N e que F_RB=5N.

02- Colocando as forças que influem no movimento:

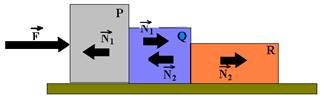
Bloco P  —  F_R=m_P.a  —  F – N₁=6.a I  —  bloco Q  —  F_R=m_Q.a  —  N₁ – N₂=4.a  II  —  bloco R  —  N₂ = m_R.a  — 

N₂ = 2.a  III  —  somando I com II com III, obtemos 48=12ª  —  a=4m/s². A força pedida tem intensidade N₂=2.a  —

N₂=2.4  —  N₂=8N

03– Vamos achar a intensidade de , considerando os 4 blocos como um só, de massa M=12kg e aplicar a lei fundamental  —  F_R=m.a  —  F=12.2  —  F=24N

Colocando as forças apenas sobre o bloco M que são F=24N e a reação a entre N e M que é N:

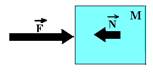
Bloco M  —  F_R=m_M.a  —  24 – N = 3.2  —  N =18N

04– Em fios a força é de tração :

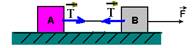
Bloco A  —  F_R=m_A.a  —  T=10.a I           bloco B  —  F_R=m_B.a  —  F – T=m_B.a  —  60 – T=20.a II  —  Somando I com II  —

60 = 30.a  —  a=2m/s², que, substituído em I ou II, fornecerá  —  T=20N      R- E

05– Bloco A  —  F_R=m.a  —  T₁ – T₂=1.10  —  T₁ – T₂=10                Bloco B  —   FR=m.a  —  T₂ – T₃=2.10  —  T₂ – T₃=20

Bloco C  —  F_R=m.a  —  T₃=3.10  —  T₃=30N, que substituído em T₂ – T₃=20  —  T₂-30=20  —  T₂=50N

T₁ – T₂=10  —  T₁ – 50=10  —  T₁=60N

06– (a) Colocando as forças que influem no movimento:

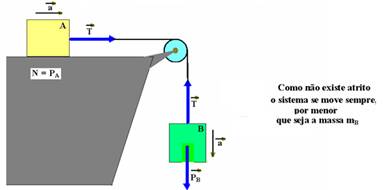
Bloco A  —  F_R=m_A.a  —  T=3.a I   —   Bloco B   —   F_R=m_B.a   —   P_B – T=m_B.a   —   m_B.g – T=m_B.a   —   1.10 – T=1.a

10 – T=a II   —   somando I com II   —   10=4.a   —   a=2,5m/s²

T=3.a   —   T=3.2,5   —   T=7,5N

b) Sobre o bloco A deixa de existir a força de tração , a força resultante sobre ele torna-se nula, ele fica em equilíbrio dinâmico

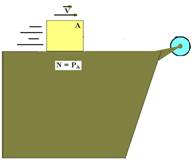
e segue em MRU com velocidade constante , até se chocar com a polia.

Sobre o bloco B deixa de existir a força de tração e a força resultante sobre ele fica sendo apenas seu peso  —  F_r =P_B  —

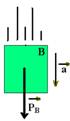
m_B.a = m_B.g  —  a = g  —  ele cai em queda livre com aceleração da gravidade.

07– Colocando o peso do bloco m₂   —   P=1.10  —P=10N

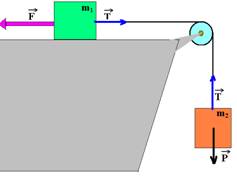
O sistema se move no sentido anti-horário, pois F>P, ou seja, m₂ sobe e m₁ se desloca para a esquerda.

Bloco m₁  —  F_R=m.a   —   F – T=m₁.a   —   40 – T=1.a   —   40 – T=a I        Bloco m₂   —   T – P=m.a   —   T – 10=1.a   —

T – 10=a II   —   somando I com II   —   40 – 10=2.a   —   a=15m/s²   —   T – 10=1.a   —   T=10 + 15   —   T=25N             

08– a)Colocando as forças:

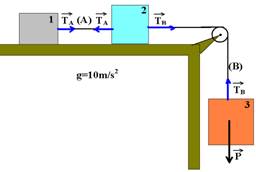
bloco 1   —   F_R=m₁.a   —   T_A=40.a I           bloco 2   —   F_R=m₂.a   —   T_B­  – T_A=20.a II       bloco 3   —   F_R=m₃.a   —

T_B – P=m₃.a   —   T_B – 600=60.a III   —   somando I com II com III   —   600=120.a   —   a=5m/s², que, substituído em III nos fornece   —   T_B=600 + 60.5   —   T_B=900N

09– a) P_A=m_A.g   —   P_A=6.10   —   P_A=60N             P_B=m_B.g   —   P_B=10.10   —   P_B=100N

Colocando as forças que agem sobre cada bloco e tirando o dinamômetro, pois sua massa é desprezível.

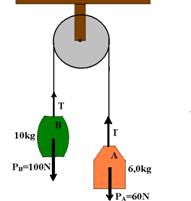
Observe que, como P_B>P_A, o sistema se move no sentido anti-horário (A sobe e B desce).

bloco A  —  F_R=m_A.a  —  T – 60=6.a I                      bloco B  —  F_R=m_B.a  —  100 – T=10.a II              somando I com II  — 

100 – 60=16.a  —  a=40/16  —  a=2,5m/s²

b) o dinamômetro indica a intensidade da força de tração no fio no qual ele está inserido, ou seja, indica T  —  T – 60=6.a  —

T=60 + 6.2,5  —  T=75N

10– R- B (veja teoria  

11– primeiro carrinho  —  F – T=40.0,5  —  F – T=20           segundo carrinho  —  T=100.0,5  —  T=50N  —  F – 50=20  —  F=70N            R- C

12– Considerando o princípio fundamental da Dinâmica, F(resultante) = massa x aceleração temos:  —  Na descida: mg – T = ma

Na subida: T’ – mg = ma  —  Isolando as trações  —  T = mg – ma = m(g – a)  —  T’ = mg + ma = m(g + a)

Então  —   T’/T = (g + a)/(g – a)

13– A aceleração de cada  bloco em cada caso é a mesma, pois F é a mesma e a massa do sistema (3m) é a mesma.

Primeira situação  —  bloco m  —  T₁=m.a I         segunda situação  —  bloco2 m  —  T₂=2m.a II

comparando I com II  —  T₂ = 2T₁  —  R- A

14– A proporção de comprimento é válida também para massa. Separando as frações:

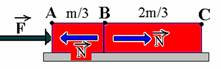
Considerando o sistema todo  —  F_R=(m/3 + 2m/3).a  —  F=(3m/3).a  —  F=m.a I

Sobre a massa m/3  —  F_R=m/3.a  —  F – N=m/3.a  —  3F – 3N=m.a  —   veja em I que F=m.a  —  3F – 3N=F  —  3N=2F  —

N=2F/3    

15– Colocando as forças:

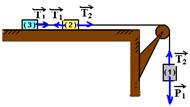
bloco3  —  T₁=ma I             bloco 2  —  T₂ – T₁=ma II              bloco 1  —  P₁ – T₂=ma III         somando I, II e III  — 

P₁=3ma  —  mg=3ma  —  a=g/3

Quando o fio que une 2 e 3 se rompe, teremos:

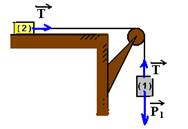
bloco 2  —  T=ma’ I          bloco 1  —  P₁ – T=ma’ II           somando I com II  —  P₁=2ma’  —  mg=2ma’  —  a’=2g

dividindo membro a membro a=g/3 por a’=2g, obtemos  —  a’/a=3/2 

16– A aceleração é a mesma nas duas situações, pois as massas e a força aplicada são as mesmas.. A força de contato será maior na situação do conjunto 1, pois o bloco da esquerda terá que empurrar uma massa maior.

17– a) As forças que atuam no balde são a tração do fio, T, e o peso P. Quando o balde está em repouso, temos T = P = 100 N. Como P = mg  —  100=m.10  —  m=10kg. . Já quando o dinamômetro acusa T = 120 N, temos, F_R=ma  —   T – P = ma, ou seja, a = (120 – 100)/10 = 2 m/s².

b) Não é possível concluir, pois só conhecemos a aceleração, e não a velocidade. Apenas sabemos que T>P, ou seja, ele pode estar subindo acelerado ou descendo retardado.

18–

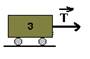
F_R=ma  —  T=2.10².2  —  T=4.10²N

19– Vamos calcular a aceleração do sistema (barco + pessoa + pacote)  —  Pela segunda lei de Newton, F_R = m.a  —   240 = (100 + 58 + 2).a  —  240 = 160.a ==> a = 240/160 = 1,5 m/s².

 

Apenas sobre o pacote de 2 kg

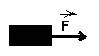
F = m.a = 2.1,5 = 3,0 N

20- O dinamômetro indica a tração no fio que é de 40N e as forças sobre o sistema estão indicadas na figura.

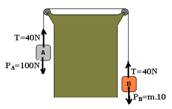
Observe no bloco A que, como P_A>T, ele deve descer e consequentemente B deve subir.

Assim, considerando que A desça acelerado, pelo princípio fundamental da dinâmica temos, para o corpo A, que:  —  F_R=m_A.a  —

100 – 40 = 10.a ==> a = 60/10 = 6 m/s².

Para o corpo B:  —  F_R=m_B.a  —  40 – m.10 = m.6  —  40 = 16.m   —  m = 40/16 = 2,5 kg

21– Bloco A                                                                                    

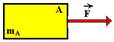
F_R=m_A.a  —  F=m_A.a I         

Bloco B sobre o bloco A

F_R=(m_A + m_B).a/4  —-  F==(m_A + m_B).a/4  —  4F=m_Aa + m_Ba  —  4F=F + m_Ba  — 3F=m_Ba II

Dividindo membro a membro II por I  —  3m_A=m_B  —  m_A/m_B=1/3

22– Calculando a aceleração do sistema pelo gráfico  —  a=DV/Dt  —  a=24/6  —  a=4m/s²

Bloco A  —  P_A – T=m_Aa  —  10m_A – T=4m_A  —  T=6m_A I          blobo B  —  T=m_Ba  — T=m_B.4 II    —   igualando I com II  —  6m_A=4m_B   —  m_A/m_B=2/3

23– a) caminhonete  —  F_R=m_c.a  —  F – T=2.000X1  —  F – T=2.000 I     caixote  —  T – 800=80X1  —  T=880N II

substituindo II em I  —  F – 880=2.000  —  F=2.880N

b) Sim, será possível, pois a tração máxima que o cabo suporta é 2000N e a tração aplicada é de 880N

 

24-1^a etapa  —  queda livre da esfera m_o, com a=g e a velocidade variando de 0 a V_o, numa queda de altura H_o.

Torricelli  —  V_o² = 0² + 2.g.H_o  —  V_o² =2gH_o            2^a etapa  —  as duas esferas se movem juntas com aceleração a que vale:

M=3m_o, se desloca para a direita puxada por T  —  F­_R=ma  —  T=3m_oa I          m_o, desce de modo que P – T=m_oa  — 

M_o.g – T=m_o.a II —  substituindo I em II  —  m_og – 3m_oa=m_oa  —  g=4.a  —  a=g/4

Queda de m_o com aceleração a=g/4 e velocidade variando de V_o a V, numa queda de altura H_o

Torricelli  —  V²=V_o² +2.a.DS  —  V²= V_o² + 2.g/4.H_o  —  V²=2gH_o + (2gH_o)/4  —  V²=V_o² + (V_o²)/4  —  V²=(5V_o²)/4  —  V=Ö5V_o/2  —  V=2,2.V_o

25– a) equilíbrio estático (força resultante nula)

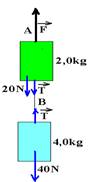
 corda B bloco de baixo  —   F_R=0   —   T=40N           bloco de cima  —  F_R=0  —  F = 20 + T  —  F = 20 + 40  —  F=60N

b) os dois blocos sobem com a=2m/s² e F_R¹0

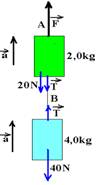
Bloco de baixo  —  F_R=ma  —  T-40=4.2  —  T=48N (tração na corda B)       bloco de cima  —  F_R=ma  —  F – T – 20=2.2  —

F – 48 – 20=4  —  F=72N (tração na corda A)

26- a) sistema em repouso  —   força que o anteparo exerce sobre A, impedindo-o de ir para a direita.

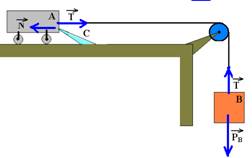
bloco B  —  P_B=T  —  T=50N           bloco A  —  N=T  —  N=50N

b) retirando-se o anteparo C, N deixa de agir sobre A e o sistema se move no sentido horário com aceleração a

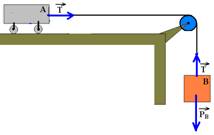
bloco A  —  F_R=ma  —  T=20.a I                   bloco B  —  F_R=ma  —  P_B – T =ma  — 50 – T =5.a II      substituindo I em II  —

50 – 20.a = 5.a  —  a=2m/s².

27- Colocando as forças sobre cada bloco:

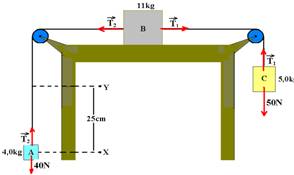
bloco A – sobe  —  F_R=ma  —  T₂  – 40= 4.a I                bloco B – direita  —  F_R=ma  —  T₁ – T₂=11.a II      bloco C – desce  —

F_R=ma  —  50 – T₁=ma  —  50 – T₁=5.a III      Somando I, II e III   —  10=20.a   — a= 0,5m/s²    

Bloco A que sobe com aceleração de 0,5m/s², percorrendo DS=25cm=0,25m e tendo V_o=0 em X e V em Y.

Torricelli  —  V² = V_o² + 2.a.DS  —  V² = 0² + 2.0,5.0,25  —  V=Ö0,25  —  V=0,5m/s

28– Colocando as forças e calculando a aceleração do sistema:

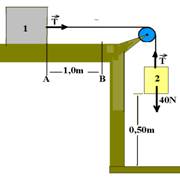
bloco 1  —  F_R=m.a  —  T=6.a I                bloco 2  —  F_R=m.a  —  40 – T=4.a II        substituindo I em II  —  40 – 6.a=4.a  —

a=4m/s².  Observe na figura que os dois blocos se movem juntos enquanto percorrem apenas 0,5m, com aceleração a=4m/s² e, no instante em que 2 chega ao solo,eles tem velocidade:

Torricelli  —  V² = V_o² + 2.a.DS  —  V²= 0² + 2.4.0,5  —  V=2m/s. A partir daí, 2 não puxa mais 1 e ele segue em MRU com velocidade constante de 2m/s, com que chega em B.

29- (1) bloco A  —  F – T=m.a  —  F – T=4.2  —  F – T=8 I           bloco B  —  T=6.2   —  T=12N II     substituindo II em I  —       

F – 12=8  —  F=20N  —  está correta

(2) está correta – vide (1)

(3) está correta, pois o dinamômetro é ideal (como se não existisse).

(4) está correta, o dinamômetro indica a tração no fio.

Todas corretas

30- colocando as  forças e, como as massas são iguais, a tração (T) em cada fio é a mesma. 

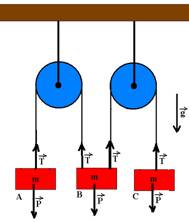
Observe na figura acima que o bloco B sobe, pois nele temos 2T para cima. Bloco A  —  desce  — P-T=ma  —  mg-T=ma I   —  bloco B  —  sobe  —  2T-P-ma  —  2T-mg=ma II  —  bloco C  —  desce  —  P-T=ma  —  mg-T=ma III  —  somando I, II e III  —  mg=3ma  —  a=g/3   R- C

31- Colocando as forças:

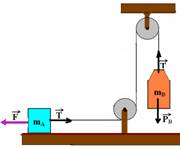
Bloco B  —  sobe  —  T – P_B = m_B.a  —  T – 100 = 10.a I                 bloco A  —  para a esquerda  —  F – T=m_A.a  — 

500 – T=15.a II  —  somando I com II  —  a=16m/s²  —  T – 100=10.16  —  T=260N  

32- a) m=100g=0,1kg   —  F-P=m.a  —  F – 3=0,3.3  —  F=3,9N.

b) só sobre o elo do meio  —  F_R=m.a  —  F_R=0,1.3  —  F_r=0,3N

c) elo de baixo  —  T-P=ma  —  T-1=0,1.3  —  T=1,3N

33- Cálculo da aceleração do sistema:

Bloco da esquerda  —  2mg – T=2ma       bloco da direita  —  T – mg=ma    resolvendo o sistema  —  mg=3ma  —  a=g/3

Torricelli —  V²= V_o² + 2.a.DS  —  V²= 0² + 2.g/3.h  —  V=Ö2.g.h/3

34- Quem está subindo é o anel do meio mais os três anéis de baixo, portanto 4 anéis de peso P=(4X0,2).10  —  P=8N

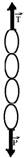
T – P=m.a  —  T – 8=0,8.2  —  T=9,6N  R- B

35-Decompondo, na figura I a força de tração T₁, observamos que:

 

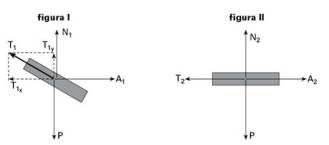
figura I  —  T_1X + N₁=P  —  N₁=P – T_1X              figura II  —  N₂=P  —  portanto N₂>N₁  —  R-B

36-Colocando as forças nas barcaças:

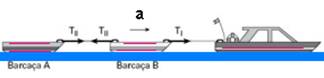
Barcaça A  —  F_R=m_A.a  —  T_II =30.10³.a  —   T_II=20.10³.a  —  8.10⁴=20.10³.a_A  —  a_A=4m/s² qualquer aceleração acima desse valor arrebenta o cabo II

O cabo I puxa as duas barcaças de massa m_A+B=50.10³kg  — F_R=m_A+B.a_B  — T_I= m_A+B.a_B  —  6.10⁵=50.10³.a_B  —  a_B=12m/s²   —  qualquer aceleração acima desse valor arrebenta o cabo I.

Como a aceleração das duas barcaças deve ser a mesma, para que os dois cabos não arrebentem temos que pegar o menor valor de a, ou seja, a=4m/s².

 

37- De uma maneira bem simples e prática  —  quando o recipiente é acelerado para a direita, o líquido, por inércia, tende a permanecer em repouso, ou seja, fica contrário ao deslocamento dos recipientes  —  R- B

38- O bloco m₂ está sujeito a 6 forças. Seu próprio peso e a força de ação F são duas delas  —  as outras quatro são devidas aos contatos com os outros dois corpos, sendo duas delas para cada corpo  —  a ação na direção da gravidade em função do peso destes corpos e ações na direção do movimento, mas no sentido oposto, por resistência a ação de F  —  R- B

39- Considere o sistema abaixo em repouso em relação a um referencial inercial em que o bloco de massa M representa o peso do cabo (aplicado em seu centro de gravidade) e as cordas representam o cabo, e q o ângulo que o cabo faz com a horizontal do lugar.

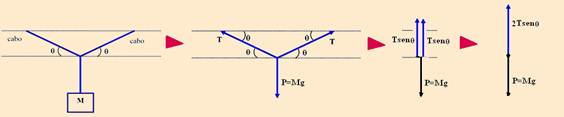
Observe na seqüência das figuras acima que, como o sistema está em equilíbrio, F_R=0  —  2Tsenθ=Mg  —  senq = Mg/2T  — 

assim, se q = 0  —   sen(q) = 0 o que significa que as forças exercidas pela corda sobre o bloco devem ser infinitas  —  ou, deve existir uma força de módulo infinito para que, somada ao peso do bloco (aqui modelando a massa do cabo), resulte zero  —  como isso não é possível, não há como se ter q = 0, isto é, deverá sempre existir, num campo gravitacional, a “curva” observada por Lucinha.

40- a) A tensão (ou tração, que é o termo mais adequado) na corda corresponde à intensidade da força aplicada por Alberto  — 

T = 200 N.

b) : força de tração no centro da polia, aplicada por Cabral  —  : forças aplicadas pela corda que passa pela polia  — 

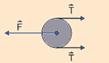
c) Como a polia não tem massa (ou seja, sua massa é desprezível) e, além disso, ela está sendo arrastada quase que estaticamente (ou seja, com velocidade constante  —  a = 0)  —   princípio fundamental  —  F_R=ma  —  F – 2 T = m a  —  F – 2 T = 0  — 

F = 2 T  = 2 (200)  —  F = 400 N.

d) A figura a seguir mostra que quando a ponta da corda desloca D (do ponto P até o ponto P’ ), o centro da polia desloca D/2.

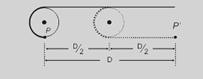
Se corda que Alberto puxa enrola D, essa distância é distribuída nos dois braços da polia, fazendo com o seu centro desloque D/2  —   portanto, se Carlos avança 2 m, Alberto recua 4 m.

41- As forças que agem sobre a esfera são seu peso (), vertical e para baixo e a força de tração no fio (), conforme figura  — 

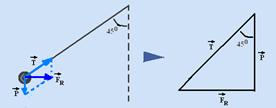
somando vetorialmente  com  você obtém a força resultante    —  tg45^o = cateto oposto/cateto adjacente  —  tg45^o=F_R/P  —  1=ma/mg  —  a=g=9,8m/s²  —  R- C

42- F_R=KV²  —  K=F_RV²=m.aV²=(m.V/t)/V²  —  K=(m/t)/V  —  K=(kg/s)/(m/s)  —  K=kg/s x s/m  —  K=kg/m  —  R- D

43- Como o andaime se encontra parado (equilíbrio estático) a resultante das forças que agem sobre ele ê nula  —   observe que os pesos sobre o andaime encontram-se no meio (peso de um operário + peso do andaime, supondo-o homogêneo) e na extremidade esquerda (peso do outro operário)  —  assim, a tensão na corda X é maior que a na corda Y  —  R- D

44- Colocando as forças que agem sobre cada bloco (pesos de A e de B, P_A e P_B, verticais e para baixo; tração T em cada bloco,

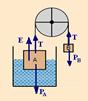
verticais e para cima e o empuxo E sobre o bloco A devido ao líquido, vertical e para cima)  —  E=ρ_liq.V_liq.g  —  E= ρ_liq.3(V/2).g  —  P_B=m.g  —  P_B= ρ_bloco.V_bloco.g  —  P_B= ρ_bloco.Vg  —  P_A=3mg=3.ρ_bloco.V.g  —  o sistema está em equilíbrio (F_R=0)  —  bloco B  —  T=P_B  —  T= ρ_bloco.Vg  —  bloco A  —  V_liq=V_bloco/2  —  V=2V  —  E + T = P_A  —  ρ_liq.3(V/2).g + ρ_bloco.Vg = 3.ρ_bloco.V.g  —  ρ_liq.3(V/2).g = ρ_bloco.2.(2V).g  —  3ρ_liq/2 = 2.ρ_bloco.2  —  ρ_liq=4 ρ_bloco/3  —  R- D

 

45-

I. Falsa  —  para que o corpo se desloque é necessário que a projeção de F na horizontal (Fcosθ) seja maior que a força de atrito  —  Fcosθ > F_atrito.

II. Correta  —  o corpo estará na iminência de se mover quando Fcosθ = F_atrito.

III. Correta  —  se F > P e θ=90^o, o bloco girará no sentido anti-horário até que a direção de F seja a mesma que de P e, a partir daí,

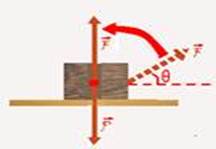
como F>P a força resultante será vertical e para cima, e o corpo subirá.

IV- Falsa  —  o corpo só será elevado se N + Fsenθ > P, pois, nesse caso sobrará uma força resultante vertical e para cima.

R- D             

46-

Aceleração de subida da plataforma A que sobe ∆S=4,5m em ∆t=3,0s, a partir do repouso V_o=0 —  ∆S=V_o.t + a.t²/2  —  4,5 =

0.3 + a.3²/2  —  a=4,4/4,5  —  a=1,0m/s²  —  esta é a aceleração de subida da massa m e de descida da massa M  —  a figura

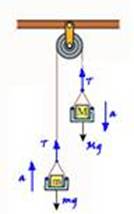
mostra as forças que agem sobre o sistema  —  equações  —  massa m  —  F_R=m.a  —  T – mg = m.a  —  T – 225.10 = 225.1  —

T=2 475N  —  massa M  —  M.g – T = M.a  —  M.10 – 2 475 = M.1  —  9M=2 475  —  M=275kg  —  R- A

47-

a) Se você considerar o sistema carro-ônibus como um sistema isolado, você pode utilizar o teorema da conservação da

 quantidade de movimento  —  Q_antes=M.V_o + m_a.V_a=9000.80 +1000.0  —  Q_antes=720000kg.m/s  —  Q_depois=(M + m_a).V=10.000.V

Q_depois=10000V  —  Q_antes = Q_depois  —  720000=10000V  —  V=72km/h.

b) Pela figura fornecida você pode determinar a intensidade da força lateral   —  sen3^o=F_L/F_at  —  0,05=F_L/8000  —  F_L=400N  

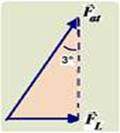
A aceleração lateral  do carro tem intensidade  —  F_L=m.a_L  —  400=1600.a_L  —  a_L=0,25m/s².

 

Voltar para os Exercícios