Resolution of Exercises on Vectors – EN
Commented resolution of exercises on vectors
01- a)
— 
— 
b) 
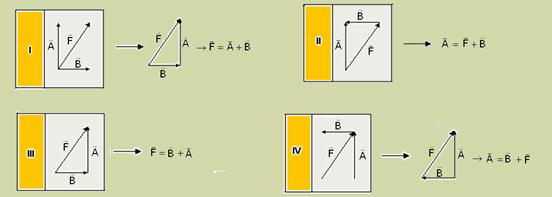
w) 
d) 
02 – Two
03- R- B — are perfectly defined by a number increased by one unit.
04- 1) displacement — vector — 2) area — scalar — 3) force — vector — 4) velocity — vector — 5) time — scalar — R- E
05- R- D
06- A
07-
Vector sum — 
R-B
08- CD + DE + EA = CB + BA — EA – CB +DE = BA – CD — R- D
09- Adding vectors using the polygonal line method
A- A
10-
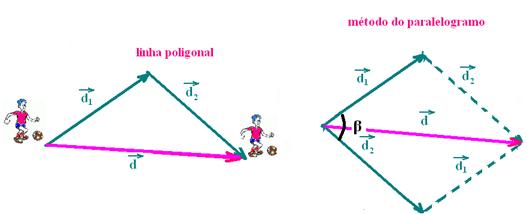
Law of cosines — d 2 =d 1 2 + d 2 2 + 2.d 1 .d 2 .cosβ — 9=3.24 + 5.76 + 8.64cosβ — 9 – 9=8.64 cosβ — cosβ= 0 — β=90 o — R- D
11-
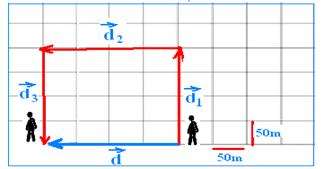
R 2 =4 2 + 6 2 — R=√52 — R- E
12- a)
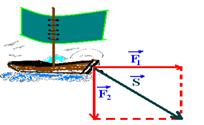
S 2 =F 1 2 + F 2 2 — 50 2 =F 1 2 + F 2 2 — 2,500=F 1 2 + F 2 2 I
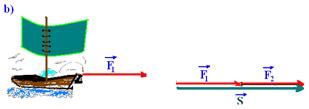
S=F 1 + F 2 — 70=F 1 + F 2 — F 1 =70 – F 2 II — II in I — 2,500=(70 – F 2 ) 2 — 2,500=4,900 – 140F 2 + F 2 2 + F 2= 2 — 2F 2 2 – 140F 2 + 2,400=0 — F 2 2 – 70F 2 + 1,200=0 — F 2 =(70±10)/2 — F 2 =30kgf and F 1 =40kgf — or — F 2 =40kgf and F 1 =30kgf
13-
Pythagoras — R – D
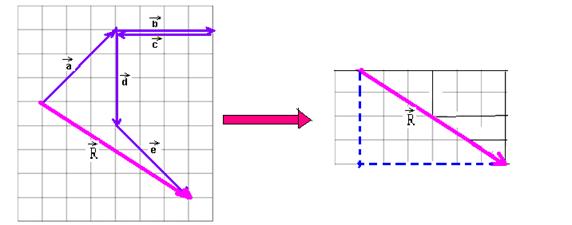
14- In the figure below is the sum of the three vectors and, to calculate the module of 
, Pythagoras is applied to the hatched triangle.
S 2 =14 2 + 6 2 — S=15.2m — R- C
15- Applying Pythagoras to the hatched triangle
+ 
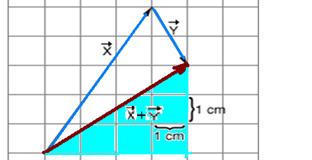
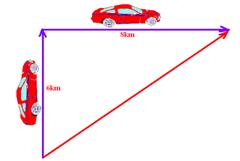
=5 — R- B
16- Dividing the hexagon as shown in the figure below and calculating the sum vector (resultant) using the polygonal line method above and
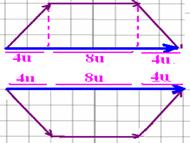
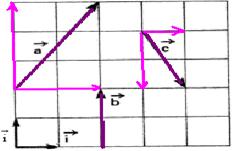
below, the vector sum of the two vectors with module 16u will be 16u + 16u=32u — R- B
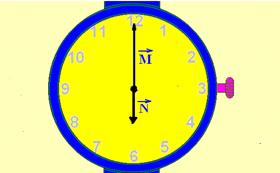
17- Dividing the hexagon and calculating the modulus of M
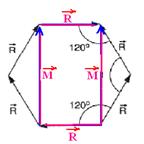
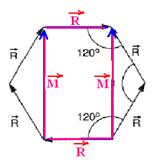
Note in the figure above that the 
upper and lower vectors cancel each other out and the sum vector will have intensity S=2M=2.3.√R — S=6√R
18- Using the polygonal line method
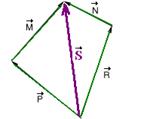
R-B
19-
— R-C
20- 
— R- D
21-
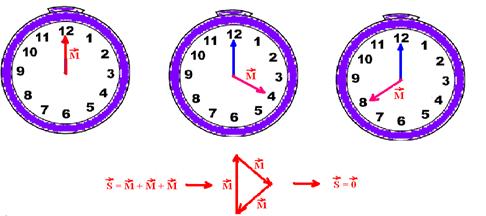
R-D
22- Calculating S and applying Pythagoras to the hatched triangle
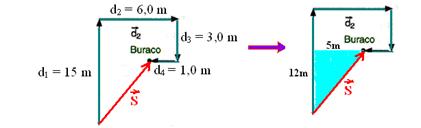
S 2 = 12 2 + 5 2 — S=13m — R- C
23 –
R- And
24- The distance traveled ΔS (car odometer indication) is given by the algebraic sum of all displacements — ΔS=5.20=100m — joining A with B we obtain the displacement vector which is calculated by applying Pythagoras to the triangle
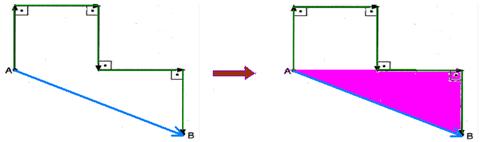
hatched — d=40 2 + 20 2 — d=√2,000 — d=20√5m — R- C
25- a) False b) True c) true d) false e) false f) true
26- R- D
27- Adding all vectors using the polygonal line method
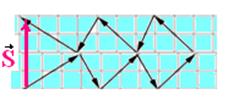
S=4.0,50=2.0cm — R- E
28-
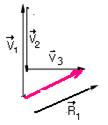
A- A
29-
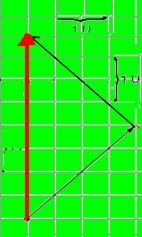
R-C
30-
R- 2 and 3
31- a)
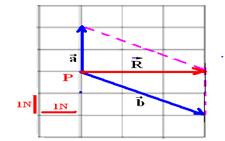
Module — R=3N
b) After the sum, the origin (P) must coincide with the end (P)
32- Since the direction and sense of these two vectors were not specified, they can be any — maximum value of R = 10 + 15 = 25N (same direction and same sense) — minimum value of R = 15 – 10 = 5N (same direction and opposite senses) — therefore R cannot be greater than 25N, nor less than 5N — R- A
33- Observe the figure below where the vectors were decomposed
R-C
34- Under the conditions of the exercise — α=45 o — law of cosines — R 2 = 70 2 + 100 2 + 2.70.100.cosα — R 2 = 4,900 + 10,000 + 14,000.√2/2 — R=157.2km — R- C
35-
R-D
36– The figure shows the displacements mentioned and the distance sought.
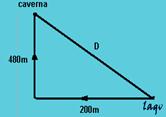
Since the triangle shown is right-angled, we just need to apply Pythagoras’ theorem — 
R-D
37-
R-B
38- a) Vector A is oriented in the same direction as vector B, that is, vectors A and B are parallel. When vectors
are in the same direction (in this example, horizontal) and the module of the resulting vector ( 
) is obtained by adding their modules, that is, C = A + B.
b) The vector 
is oriented in a direction perpendicular to the vector 
. When the vectors are perpendicular, the sum of the
squares of their modules is equal to the square of the module of the resulting vector, that is, C 2 = A 2 + B 2 .
39- The graphic scale states that each centimeter of the map is equivalent to 250 kilometers of terrain, which makes it easier to represent
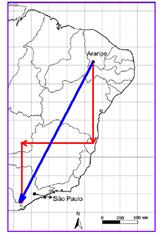
vectorially the route taken by the traveler and even represent his vector displacement (in blue). In this way, he walked 1000 km to the South (an easy direction to identify, since the North is indicated on the map), leaving Ceará and passing through Pernambuco and Bahia. In this state, he changed course and traveled 1,000 km to the West, arriving in Goiás, from where he headed another 750 km to the South, arriving in the state of São Paulo. On this route, the traveler saw the ecosystems of the Caatinga, the Cerrado and the Atlantic Forest.
R- And
40-
To calculate the intensity of the resulting force acting on the cosmic particle you can decompose the forces in the north and east directions — note in the sequence below that the intensity of the resulting force is 1N in the east direction —
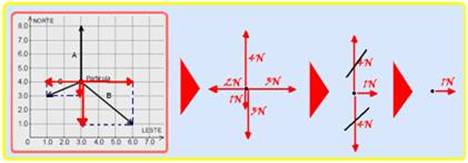
Since the initial velocity of the particle has intensity V o = 1200 m/s from north to south and the resulting force on it has intensity 1N from west to east, the movement of the particle has the characteristics of a composition of two movements, one in the east direction and the other in the south direction (see figure) — in the east direction, the projection of the initial velocity is zero V oL = 0 and it moves under the action of a resulting force of value F R = 1N and with acceleration — F R = ma — 1 = 2.10 -3 .a — a = 500 m/s 2 — its velocity in this direction after t = 1s will have intensity — V L = V oL + a L .t = 0 + 500.1 — V L = 500 m/s — in the south direction it will be thrown downwards with V oS = 1200 m/s, accelerating with the acceleration of gravity g = 10 m/s 2 — after t = 1s, its velocity in this direction will be — V S = V oS + gt = 1200 + 10.1=1210m/s —
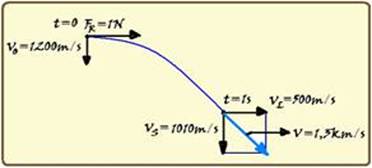
note in the figure that these two speeds are perpendicular and, applying Pythagoras you will obtain V 2 = V L 2 + V S 2 =(500) 2 + (1210) 2 — V=√(1714100) — V=1309m/s=1.3km/s — R- A .
41 – By the principle of inertia, if the forces cease to act, the resulting force on it will be zero and, after that instant, by inertia, it will continue in MRU at a constant speed of 1.3 km/s — note in the resolution of the previous exercise (08) that, before 1 s the trajectory was parabolic — R- D.
42- The vector sum of 
with 
gives the speed 
of the plane relative to the ground — note in the figure that θ +
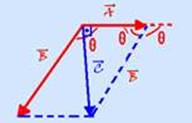
θ’=180 o —cosθ’=cos(180 – θ)= – cos θ — – cosθ=adjacent side/hypotenuse=A/B — cosθ= – A/B — R- C