Resolução dos Exercícios sobre Vetores
Resolução comentada dos exercícios sobre vetores
01- a)
— 
— 
b) 
c) 
d) 
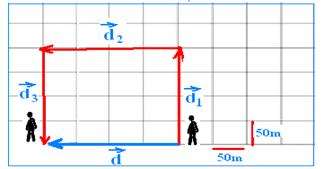
02– Dois
03- R- B — são perfeitamente definidas por um número acrescido de uma unidade.
04- 1) deslocamento — vetorial — 2) área — escalar — 3) força — vetorial — 4) velocidade — vetorial — 5) tempo — escalar — R- E
05- R- D
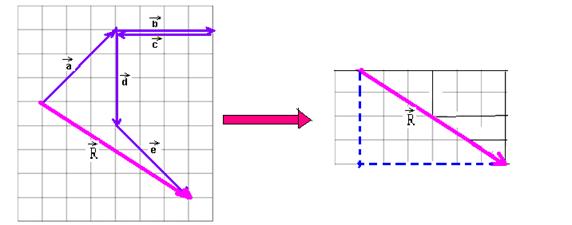
06- A
07-
Soma vetorial — 
R- B
08- CD + DE + EA = CB + BA — EA – CB +DE = BA – CD — R- D
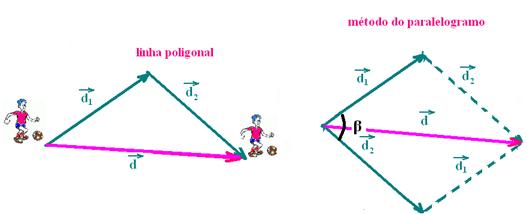
09- Somando os vetores pelo método da linha poligonal
R- A
10-
Lei dos cossenos — d2=d12 + d22 + 2.d1.d2.cosβ — 9=3,24 + 5,76 + 8,64cosβ — 9 – 9=8,64 cosβ — cosβ=0 — β=90o — R- D
11-
R2=42 + 62 — R=√52 — R- E
12- a)
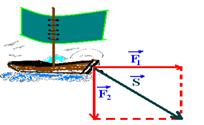
S2=F12 + F22 — 502=F12 + F22 — 2.500=F12 + F22 I
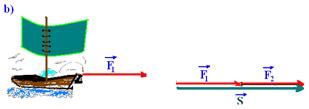
S=F1 + F2 — 70=F1 + F2 — F1=70 – F2 II — II em I — 2.500=(70 – F2)2 — 2.500=4.900 – 140F2 + F22 + F2=2 — 2F22 – 140F2 + 2.400=0 — F22 – 70F2 + 1.200=0 — F2=(70±10)/2 — F2=30kgf e F1=40kgf — ou — F2=40kgf e F1=30kgf
13-
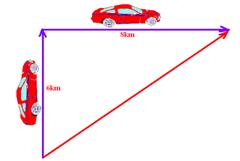
Pitágoras — R– D
14- Na figura abaixo está a soma dos três vetores e, para calcular o módulo de 
, aplica-se Pitágoras no triângulo hachurado.
S2=142 + 62 — S=15,2m — R- C
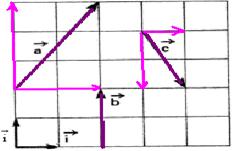
15- Aplicando Pitágoras no triângulo hachurado
+
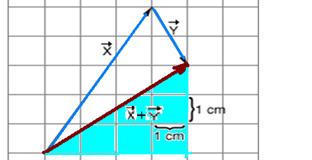
=5 — R- B
16- Dividindo o hexágono conforme a figura abaixo e calculando o vetor soma (resultante) pelo método da linha poligonal em cima e
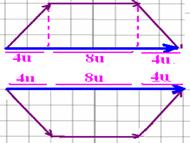
em baixo, o vetor soma dos dois vetores de módulo 16u será 16u + 16u=32u — R- B
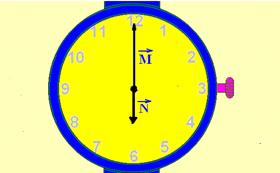
17- Dividindo o hexágono e calculando o módulo de M
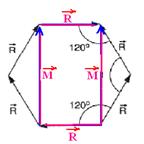
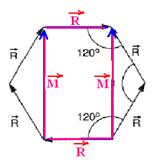
Observe na figura acima que os vetores 
de cima e de baixo se anulam e o vetor soma terá intensidade S=2M=2.3.√R — S=6√R
18- Usando o método da linha poligonal
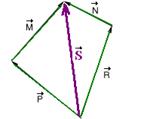
R- B
19-
— R- C
20- 
— R- D
21-
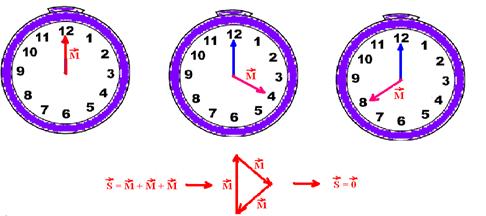
R- D
22- Calculando S e aplicando Pitágoras no triângulo hachurado
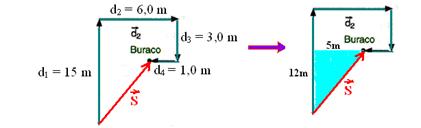
S2 = 122 + 52 — S=13m — R- C
23–
R- E
24- A distância percorrida ΔS (indicação do odômetro do carro) é fornecida pela soma algébrica de todos os deslocamentos — ΔS=5.20=100m — unindo A com B obtém-se o vetor deslocamento que é calculado aplicando-se Pitágoras no triângulo
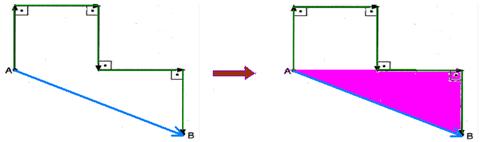
hachurado — d=402 + 202 — d=√2.000 — d=20√5m — R- C
25- a) Falsa b) Verdadeira c) verdadeira d) falsa e) falsa f) verdadeira
26- R- D
27- Somando todos os vetores pelo método da linha poligonal
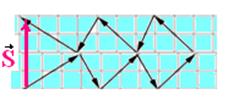
S=4.0,50=2.0cm — R- E
28-
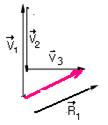
R- A
29-
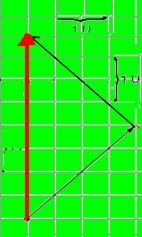
R- C
30-
R- 2 e 3
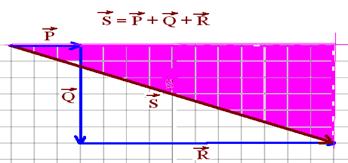
31- a)
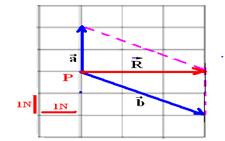
Módulo — R=3N
b) Após a soma, a origem (P) tem que coincidir com a extremidade (P)
32- Como não foi especificado a direção e o sentido desses dois vetores, eles podem ser quaisquer — valor máximo de R=10 + 15=25N (mesma direção e mesmo sentido) — valor mínimo de R=15 – 10=5N (mesma direção e sentidos contrários) — portanto R não pode ser superior a 25N, nem inferior a 5N — R- A
33- Observe a figura abaixo onde os vetores foram decompostos
R- C
34- Nas condições do exercício — α=45o — lei dos cossenos — R2 = 702 + 1002 + 2.70.100.cosα — R2 = 4.900 + 10.000 + 14.000.√2/2 — R=157,2km — R- C
35-
R- D
36– A figura mostra os deslocamentos citados e a distância procurada.
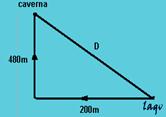
Como o triângulo mostrado é retângulo é só aplicarmos o teorema de Pitágoras — 
R- D
37-
R- B
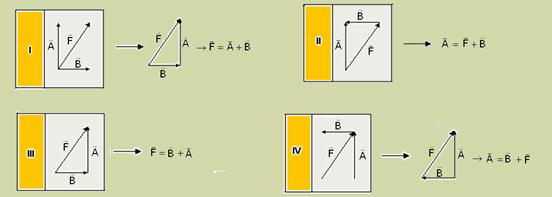
38- a) O vetor A está orientado na mesma direção e sentido do vetor B, ou seja, os vetores A e B são paralelos. Quando os vetores
se encontram na mesma direção e sentido (neste exemplo, horizontal) e o módulo do vetor resultante (
) é obtido somando-se os seus módulos, ou seja, C = A + B.
b) O vetor 
está orientado em uma direção perpendicular ao vetor 
. Quando os vetores são perpendiculares, a soma dos
quadrados dos seus módulos é igual ao quadrado do módulo do vetor resultante, ou seja, C2 = A2 + B2.
39- A escala gráfica dispõe que cada centímetro do mapa equivale a 250 quilômetros do terreno, o que facilita representar
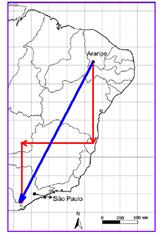
vetorialmente o percurso feito pelo viajante e, inclusive representar seu deslocamento vetorial (em azul). Dessa forma ele caminhou 1000 km para o Sul (direção fácil de identificar, pois o Norte está indicado no mapa), saindo do Ceará e passando por Pernambuco e Bahia. Nesse estado mudou de rumo e viajou 1.000 km para o Oeste, chegando a Goiás, a partir de onde rumou mais 750 km para o Sul, chegando ao estado de São Paulo. Nesse trajeto o viajante avistou os ecossistemas da Caatinga, do Cerrado e da Mata Atlântica.
R- E
40-
Para calcular a intensidade da força resultante que age sobre a partícula cósmica você pode decompor as forças nas direções norte e leste — observe na sequência abaixo que a intensidade da força resultante é de 1N no sentido leste —
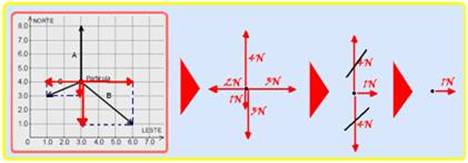
Como a velocidade inicial da partícula tem intensidade Vo=1200m/s do norte para o sul e a força resultante sobre ela tem intensidade 1N do oeste para leste, o movimento da partícula tem as características de composição de dois movimentos, um no sentido leste e outro no sentido sul (veja figura) — no sentido leste, a projeção da velocidade inicial é nula VoL=0 e ela se desloca sob ação de uma força resultante de valor FR=1N e com aceleração — FR=m.a — 1=2.10-3.a — a= 500m/s2 — sua velocidade nessa direção após t=1s terá intensidade — VL=VoL + aL.t=0 + 500.1 — VL=500m/s — no sentido sul ela será lançada para baixo com VoS=1200m/s, acelerando com aceleração da gravidade g=10m/s2 — após t=1s, sua velocidade nessa direção será — VS=VoS + g.t=1200 + 10.1=1210m/s —
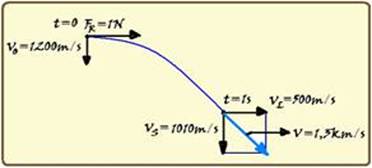
observe na figura que essas duas velocidades são perpendiculares e, aplicando Pitágoras você obterá V2 = VL2 + VS2=(500)2 + (1210)2 — V=√(1714100) — V=1309m/s=1,3km/s — R- A.
41– Pelo princípio da inércia, se as forças deixarem de atura, a força resultante sobre ela será nula e, após esse innstante, por inércia, ela seguirá em MRU com velocidade constante de 1,3km/s — observe na resolução do exercício anterior (08) que, antes de 1s a trajetória era parabólica — R- D.
42- A soma vetorial de 
com 
fornece a velocidade 
do avião em relação ao solo — observe na figura que θ +
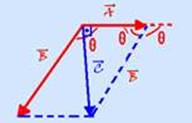
θ’=180o —cosθ’=cos(180 – θ)= – cos θ — – cosθ=cateto adjacente/hipotenusa=A/B — cosθ= – A/B — R- C