Velocidade escalar média e ultrapassagens – Resolução
Velocidade escalar média e ultrapassagens
Resoluções
01- Vm=ΔS/ Δt=(SB – SA)/(tB – tA)=70 – (-40)/6,0 – 1,0 — Vm=22m/s
02- Primeiro trecho — Vm1=ΔS1/Δ1 — 54= ΔS1/1 — ΔS1=54km — tempo de parada – Δp=0,5h — segundo trecho — Vm2=ΔS2/Δt2 — 36= ΔS2/0,5 — ΔS2=18km — VmT=ΔSt/ΔtT=(54 + 18)/(1 + 0,5 + 0,5) — VmT=36km/h/3,6=10m/s — R- A
03- Vm=ΔS/Δt — 4=1.000/Δt — Δt=1.000/4=250/24=10,4 dias — R- B
04- Aplicando Pitágoras — ΔS2= 82+ 62 — ΔS=10m

Vm=10/20 — Vm=0,5m/s
05- ΔS=245 – 200 — ΔS=45km — Δt=0,5h — Vm=45/0,5 — Vm=90km/h — R- B
06- dtotal=dA + dB +dC
I — Vtotal=(dA + dB + dC)/(tA + tB + tC) — Vtotal=( dA + dB + dC)/(dA/VA + dB/VB + dC/VC)
II — dividindo I por II — I/II= ( dA + dB + dC)/X(dA/VA + dB/VB + dC/VC)/ ( dA + dB + dC) — R- A
07- Tendo ou não fio, a ida é através de ondas eletromagnéticas e, nesta distância, a propagação é instantânea e portanto leva-se em conta apenas a volta do som pelo ar com velocidade de 330ms — 330=330/Δt — Δt=1s — R- A
08- a) Deve percorrer 400m na horizontal e 300m na vertical

ΔSmínima= 400 + 300 — ΔSmínim=700m
b) O deslocamento do metrô vale ΔS2=4002 + 3002 — ΔS=500m — 36/3,6=500/Δt — Δt=500/10 — Tm=50s
c) carro — 18/3,6=700/Tc — Tc=140s — Tc/Tm=140/50 — Tc/Tm=2,8
09- a) Observe no gráfico que as rodas da frente demoram Δt=0,1s para pressionar os sensores S(1) e depois S(2), percorrendo ΔS=2m — V=2/0,1 — V=20m/s=72km/h
b) As rodas dianteiras e as traseiras demoram Δt=0,15s para passarem por um dos sensores com velocidade de 20m/s — 20= ΔS/0,15 — ΔS=3m
10- 1ano=365diasX24hX3.600s — 1 ano=31.536.000s — 10 milênios=10X1000X31.536.000=315.360.000.000s — 10 milênios = 3,1536.1011s — V=ΔS/ Δt — 3.108= ΔS/ 3,1536.1011 — ΔS=9,4608.1011 — ΔS=10.1011.108=1020m = 1017km — R- B
11- 1ano=365diasX24hX3.600s — 1 ano=31.536.000s — 10 milênios=10X1000X31.536.000=315.360.000.000s — 10 milênios = 3,1536.1011s
— V=ΔS/ Δt — 3.108= ΔS/ 3,1536.1011 — ΔS=9,4608.1011 — ΔS=10.1011.108=1020m = 1017km — R- B
12- Tempo que ele demora para percorrer o trecho total — Vmtotal= ΔStotal/ Δttotal —
80=40/ Δttotal — Δttotal=0,5h — nos primeiros 15min, com velocidade média de 40km/h, ele percorreu — V1=ΔS1/Δt1 — 40= ΔS1/(15/60) — ΔS1=10km
— falta percorrer — ΔS2=(40 – 10)=30km em Δt2=(0,5 – 0,25)=0,25h — V2=30/0,25 — V2=120km/h — R- C
13- 5=ΔS/20 — Δs=100m
14- a) 1.540=2.0,1/Δt — Δt=0,0013 — Δt=1,3.10-3 s
b) 1.540=d/0,25.10-4(só volta) — d=3,85cm — d’=10 – 3,85 — d’=6,15cm
15- A resolução desse exercício envolve o conceito de velocidade relativa, explicado pelas figuras abaixo:
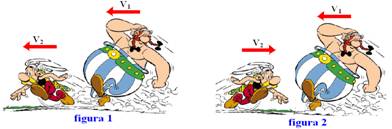
Na figura 1 onde eles se movem no mesmo sentido, a velocidade relativa entre eles (velocidade com que 2 se afasta de 1) vale VR1=V2
– V1 — 100/1=V2 – V1 — 100=V2
– V1 I — na figura 2, onde eles se movem em sentidos contrários, a velocidade relativa entre eles (velocidade com que 2 se aproxima de 1) vale — VR2=V2 + V1 — 90/0,1=V2
+ V1 — 900=V2 + V1 —
V2=900 – V1 II — substituindo II em I — 100=(900 – V1) – V1 — 2V1=800 — V1=400cm/s=4m/s — V2=900 – 400 —
V2=500cm/s=5m/s — R- C
16- Ida — Vi=ΔSi/Δti — 70=7/Δti — Δti=1/10h — trecho total — Vt=ΔSt/Δtt — Vt= (7 + 6)/(1/10 + 1/3) —Vt=13/(3 + 10)/30 — Vt=30km/h — volta — Vv=ΔSv/Δtt — Vv=13/(1/6) — Vv=78km/h — R- A
17- Distância percorrida por cada um desses instantâneos — ΔS=2.4,2.1010m — o intervalo de tempo entre esses 12 instantâneos foi de 11 idas e voltas — 11.34min=11X2.040 — Δt=22.440s — V=ΔS/Δt — 35.000=ΔS/22.440 — ΔS=785.400.000m — ΔS=785.400km — ΔS=7,9.105km
18-
1a metade — V1=ΔS1/Δt1 — 60=d/ Δt1 — Δt1=d/60 —
2a metade — V2=ΔS2/Δt2 — 90=d/ Δt2 — Δt2=d/90 —

Vtotal=ΔStotal/ Δttotal — Vtotal=2d/(d/60 + d/90)=2d/(5d/180) — Vtotal=2dX180/5d
— Vtotal=72km/h
19- Observe que durante todo o percurso de 15km o metrô ficou parado durante 5 minutos (1 minuto em cada estação com exceção do Bosque “de onde partiu” e do Terminal “onde chegou”) — de Vila Maria de onde partiu quando t=1 minuto até Felicidade onde chegou quando t=5 minutos ele demorou Δt=(5 – 1)=4s e percorreu ΔS=2km — V=2/4 — V=0,5km/h (durante todo o prrcurso, pelo enunciado) — tempo que demora para percorrer o trecho total de 15km com velocidade média de 0,5km/h — 0,5=15/Δt — Δt=30 minutos — Δttotal=30 (tempo de movimento) +
5 (tempo parado) — Δttotal=35 min — R- D
20- Cálculo da altura h do nível do mar ao satélite — V= 3.108m/s — Δt=18/2.10-4 =9.10-4s (só volta) — 3.108=h/9.10-4 —

h=27.104m — cálculo da altura h’ do topo da geleira até o satélite — 3.108=h’/8,9.10-4 — h’=26,7.104 — altura da geleira — hgeleira=27.104–26,7.104 — hgeleira=0,3.104=3.000m
21- Velocidade da pessoa — V=1,5.70cm/1s — V=105cm/s — ΔS=21m=2.100cm — 105=2.100/Δt — Δt=20s — R- C
22- Em 15min=15/60=1/4h ele percorre — 90=d1/(1/4) — d1=22,5km(sem chuva) — 60=d2(1/4) — de2=15km (com chuva) — ele deixou de percorrer d3=22,5 – 15,0=7,5km e esse deslocamento a 90km/h demora — 90=7,5/Δt — Δt=(7,5/90)X60 — Δt=5 min — R- A
23- Tempo de percepção no ar — 340=17/Δt — Δt=0,05s — esse tempo é o mesmo independente do meio — 1600= ΔS/0,05 — ΔS=80m — R- C
24- Cada quarteirão tem lado ℓ2=10.000 — ℓ=100m — cada rua tem largura 10m e o comprimento total da procissão é de 240m — distância total percorrida — d=100 + 10 + 240 — d=350m — V=d/Δt — 0,4=350/ Δt — Δt=875/60 — Δt=14,6min R- E
25- 100= ΔS1/2 — ΔS1=200km — 80= ΔS2/1,5 — ΔS2=120km — Vtotal= ΔStotal/ Δttotal=(200 + 120)/(2 + 0,5 + 1,5) — Vtotal=80km/h — R- A
26- Em todo hexágono regular o raio R é igual ao lado ℓ e ele é formado por 6 triângulos eqüiláteros, cada um com ângulo de 60o —
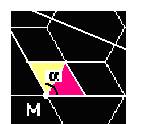
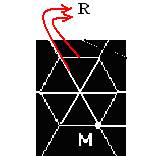
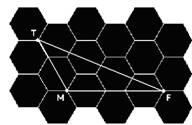
α=60o + 60o — α=120o — R=10cm — TM=30cm — MF=50cm — lei dos cossenos — (FT)2 =(TM)2 + (MF)2 -2.(TM).(MF).cos120o — (FT)2=900 + 2500 – 2.30.50.(-1/2) = 4.900 — FT = 70cm — V=70/10 — V=7cm/s — R- D
27- 1a etapa – V=(1/9).d/Δt1 — Δt1=d/9V — 2a etapa – 2V=(8/9).d.Δt2 — Δt2=4d/9V — trecho total — Vt=d/(d/9V + 4d/9V) — Vt=d/(5d/9V) — Vt=d.9V/5d — Vt=9V/5 — R- A
28-a) Para atravessar um farol a distância percorrida por um ponto P fixo em qualquer ponto do trem é ΔS=x=100m — 20=100/Δt — Δt=5s
b) Observe na figura abaixo que, para atravessar totalmente o túnel um ponto P fixo em qualquer parte do trem deve percorrer

a distância – ΔS= x(comprimento do trem) + c(comprimento do túnel “ponte”) — ΔS= (200 + 100) — V= ΔS/ Δt — 20=(300/ Δt) — Δt=15s
29- Diferença entre as velocidades – mesmo sentido – VR=(V2 – V1)=ΔS/Δt — (V2 – V1)=(10 + 10)/4 — (V2 – V1)=5m/s

R- C
30- VR=ΔS/Δt — 2V – V=100/Δt — Δt=100/V (tempo que ele demora para ultrapassar o vagão) — Vhomem=2V=ΔShomem/Δt —
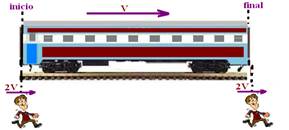
2V= ΔShomem/(100/V) — ΔShomem=200V/V — ΔShomem=200m
31- Sentidos opostos — VR=18 + 27=45km/h/3,6=12,5 — VR=12,5m/s — 12,5= ΔS/ Δt — 12,5=(200 + 250)/ Δt — Δt=36s — R- C
32- 50/3,6=(120 + d)/15 — 750=3,6d + 432 — d=318/3,6 — d=88,33m — R- B
33- VR=(20 – 15)=100/Δt — Δt=20s — R- C
34- Sentidos opostos — VR=2V + V=3V — parando o trem menor e consequentemente a pessoa, o trem maior de velocidade relativa 3V e comprimento 90m demora 2s na ultrapassagem — 3V=90/2 — V=15m/s (velocidade do trem maior) — como o trem menor tem o dobro da velocidade — V’=30m/s
35- VR=Vn – 2=50/20 — Vn=2 + 2,5 — Vn=4,5m/s — R- D
36- Como os caminhões deslocam-se em sentidos opostos, o módulo da velocidade relativa entre eles é a soma de suas velocidades — vr = 50 + 40 = 90 km/h = 25 m/s — essa é a velocidade com que o caroneiro vê o segundo caminhão passar por ele — comprimento desse caminhão — L = vr.Δt = 25.(1) — L = 25 m — R- A
37- Comprimento de cada volta — L = 27 km — c = 3.105 km/s — n = 11.103 voltas — Δt = 1 s:
a) V=ΔS/Δt — V=nL/Δt=11.000×27/1 — V=2,97.105km/s
b) A razão percentual dessa velocidade em relação à velocidade da luz é:
rp =V/cx100=2,97.105/3.105x100 — rp=99%
c) A corrida em busca de novas armas envolve tecnologias nucleares. Assim, um primeiro interesse das nações envolvidas é bélico. Além disso, a descoberta de novas tecnologias também pode ser aproveitada no desenvolvimento de novos produtos, ou mesmo na redução dos custos de produção, melhorando o poder aquisitivo e a qualidade de vida das pessoas. Há ainda um outro interesse que é a busca por novas fontes para produção de energia.
38- I. Errada — 1 ano-luz é a distância que a luz percorre em 1 ano, no vácuo, com velocidade c=3.108m/s=3.105km/s — d = v t — d = (3.105 km/s)x(2,5.106 anosx3.107 s/ano) — d=2,25.1019 km.
II. Correta — veja os cálculos efetuados no item anterior.
III. Correta.
R- E
39- V=ΔS/Δt — 5=2/Δt — Δt=2/5=0,4h — Δt=0,4×60=24min — R- C
40 – Observe pela equação da posição da formiga em função do tempo Sf=2 + 5t + 4t2 que a posição inicial da formiga é So=2mm e ela se desloca no sentido das posições crescentes do eixo (Vof=5mm/s, positiva) — como a lesma está a 16mm da formiga e se move no mesmo sentido que ela, a lesma só pode estar na posição inicial Sol=18mm — a condição para que isso ocorra está esquematizada na figura — a lesma, que tem velocidade constante de Vl=5mm/s está em movimento uniforme e sua equação
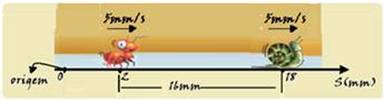
da posição em função do tempo é Sl = Sol + VoL.t — Sl=18 + 5t — no encontro elas ocupam a mesma posição, ou seja, Sf = Sl 2 + 5t + 4t2 = 18 + 5t — 4t2 = 16 — t=2 s — R- B
41- No primeiro trecho a distância percorrida foi de 75% de 800m — ∆S1=0,75×800=600m — essa distância ∆S1=600m foi perorrida no intervalo de tempo de ∆t1=(1,717 – 0,417)=78s — a velocidade média pedida é a do primeiro trecho — Vm1=∆S1/∆t1=600/78=7,7m/s
R- B
42- Considere TSE um triângulo em cujos vértices estão localizados, respectivamente, Tóquio, Sendai e o Epicentro — a
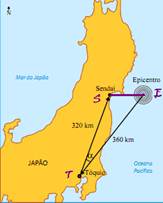
distância SE pode ser calculada utilizando-se o teorema dos cossenos
— SE2 = TS2 + TE2 – 2.TS.TE.cosα=3202 + 3602 – 2.320.360.0,934
— ES2 = 102 400 + 129 600 – 2.(25.10).(22.32.10).93,4/100
— ES2 = 16 900
— ES = 130 km
— Vm=ES/∆t=130/(13/60)
— Vm=600 km/h
— R- E
43- Ciclones — vento circular forte, produzida por grandes massas de ar em alta velocidade de rotação — os furacões são os ciclones que surgem no mar do Caribe (oceano Atlântico) ou nos EUA — os ventos circulares gerados em torno dos ciclones precisam ter mais de 119 km/h para uma tempestade ser considerada um furacão, como foi o caso do Katrina — dados — velocidade de translação do Katrina — V=24km/h — distância a ser percorrida — ∆S=1 200km — V=∆S/∆t — 24=1 200/∆t — ∆t=1 200/24=50h — R- E
