Equação horária da velocidade de um MUV – Resolução

Resolução dos exercícios sobre:

Equação horária da velocidade de um MUV

Gráfico da velocidade de um MUV

 

01- a)

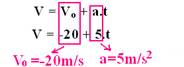
b) Quando ele muda o sentido se seu movimento ele pára (V=0) e, a partir desse instante, o movimento que era progressivo se torna retrógrado  —  V=-20 + 5t  —  0=-20 + 5t  —  t=4s (instante em que ele pára para inverter o sentido do movimento)

c)

d) 2s – retrógrado retardado  —  10s – progressivo acelerado  —  Veja esquema acima)

02- a) V_o=-8m/s  —  a=(8 – (-8))/(4 – 0)  —  a=16/4  —  a=4m/s²  

b) V= V_o + at  —  V=-8 + 4t  —  inverte o sentido (pára) – V=0  —  0=-8 + 4t  —  t=2sou pelo gráfico que corresponde ao ponto onde a reta intercepta o eixo t.

c) entre 0 e 2s  —  retrógrado (V<0) e retardado (módulo de V está diminuindo)  —  após 2s  —  progressivo (V>0) e acelerado (módulo de V está aumentando)

d) ΔS=área entre 0 e 4s, que corresponde à soma das áreas hachuradas da figura abaixo

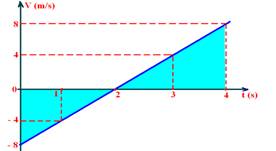
ΔS=b.h/ + b.h/2=2.(-8)/2 + 8.2/2  —  ΔS=0

03- V_o=2m/s  —  a=1ms²  —  V=V_o + at  —  V=2 + 1.8  —  V=10m/s

04- ΔS=área=(10 + 6).12,5/2  —  ΔS=100m  —  V_m=ΔS/Δt  —  V_m=10m/s  —  R- B

05- A – ΔS_A=área do trapézio=100m

ΔS_A=(t_A + (t_A – 4)).11/2  —  100=2t_A – 4).11/2  —  t_A=244/22  —  t_A=11,1s (treino A)

B – ΔS_B=área do trapézio=100m

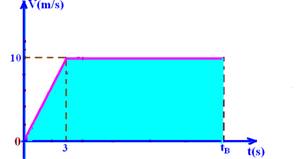
ΔS_B=(t_B + (t_B – 3)).10/2  —  100=10t_B – 15  —  t_B=115/10  —  t_B=11,5s (treino B)

Δt=t_B – t_A=0,4s  —  R- B

06- a) V_o=0  —  a=(V – V_o)/(t – t_o)=10/5  —  a=2m/s²  —  V = V_o + a.t  —  20=0 + 2t  —  t=10s

b) o deslocamento é fornecido pela área

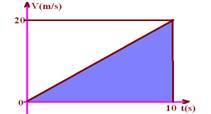
ΔS=b.h/2=10.20/2  —  ΔS=100m

07- T=5s  —  V=50 – 10.5  —  V=0  —  a=-10m/s² (constante)  —  R- C

08- V_o=10m/s  —  a=ΔV/Δt=(60m/s)/60s  —  a=1m/s²  —  V=V_o + at=10 + 1.30  — V=40m/s

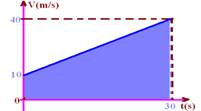
ΔS=(B + b).h/2=(40 + 10).30/2  —  ΔS=750m  —  V_m= ΔS/Δt=750/30  —  V_m=25m/s

09- I – Falsa – é no sentido contrário ao do movimento – a velocidade está diminuindo

II –

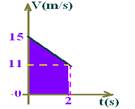
ΔS=(15 + 11).2/2=26m  —  Falsa

III – a=(9 – 15)/3=-2m/s²  —  Falsa

iV – Correta – observe que à medida que a velocidade diminui o tempo aumenta

V – V= V_o + at  —  0=15 – 2t  —  t=7,5s  —  Correta

R- D

10- entre 0 e 5s  —  V= V_o + at=0 + 4.5  —  V₅=20m/s  —  de 5s a 8s V vale 20m/s  —  a partir de 8s – a=-2m/s² até ele parar V=0  — V=V_o + at  —  0=20 -2t  —  t=10s (de 8s até ele parar)  —  desde o inicio do movimento  — t=8 + 10=18s  —  R- E

11- ΔS=área hachurada da figura abaixo

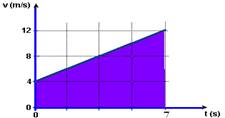
ΔS=(12 + 4).7/2 = 56m

12- a) O ângulo α que a reta representativa da velocidade forma com um eixo horizontal é tal que tgα=ΔV/Δt corresponde à aceleração do

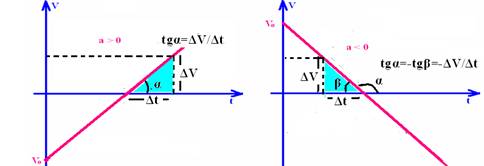
móvel, pois a= ΔV/ Δt e é denominada coeficiente angular da reta ou declividade da reta. Observe que, se α é agudo, f(t) é crescente e a>0 e se α é obtuso , f(t) é decrescente e a<0.

b) Em todo gráfico VXt a área entre a reta representativa e o eixo dos tempos é numericamente igual à variação de espaço ΔS, entre dois instantes quaisquer t₁ e t₂

 

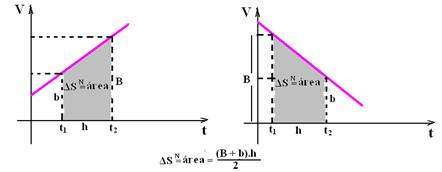
13- a) ΔS=área total=b.h/2 + (B + b).h/2 + b.h/2=3.8/2 + (4 + 2).12/2 + 2.12/2=1260  —  12 + 36 + 12=60m  —  ΔS=60m

b) V_m=60/16=3,75  —  V_m=3,75m

14- Entre 0 e 4s  —  a=4m/s²  —  V=V_o + at=0 + 4.4  —  V=16m/s  —  entre 4s e 8s  —  V= V_o + at  —  V=16 + (-2).4  —  V=8m/s

15- Quando t=0 a distância entre eles é de 32m  —  quando t=4s  —  ΔS_A=área do trapézio=(30 + 15).4/2   —  ΔS_A=90m  —  ΔS_B=área do retângulo=4.15=60m  —  antes – ΔS_a=32m  —  depois – ΔS_d=(90 – 60)=30m  —  a distância entre eles no final da frenagem será de d=32 – 30=2m  —  R- B 

16- ΔS_A=b.h/2=6.20/2=60m  —  ΔS_B=B + b).h/2=(8 + 2).10/2=50m  — ΔS_C=b.h/2=4.20/2=40m  —  R- A

17- ΔS=1.200=área do trapézio=(B + b).h/2=(90 + (90 – t)).20/2  —  1.200=(180 – t).10  —  1200=1800 -10t  —  t=60s  —  R- C  

18- Trata-se de um MUV em que a velocidade aumenta de 2,3m/s em cada 1s e, assim, sua aceleração vale a=2,3m/s²  —  V_o=6,20m/s  —  V= V_o + at  —  V=6,20 + 2,3t  —  t=3,60s – V=6,20 + 2,3.3,60  —  V=14,48m/s  —  t=5,80s – V=6,20 + 2,3.5,80  — V=19,54m/s

R- C

19- Se, na ida ela tem velocidade de 50m/s, na volta deverá ter velocidade de -50m/s  —  na ida, até parar (V=0) ela demorou  — 

V=V_o + at  —  0=50 – 0,2t  —  t=250s (na ida)  —  na volta  —  V₀=0 e V=-50m/s  —  V=V_o + at  —  -50=0 -0,2t  —  t=250s (na volta)  —  t_pedido=t_ida + t_volta  —  t_pedido=250 + 250=500s  —   t=500s  —  R- A

20- Colocando no gráfico  —  t=0 – V_o=10m/s  —  V=0  —   0=10 -2t  —  t=5s

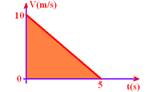
ΔS=área=b.h/2=5.10/2  —  ΔS=25m  —  R- D

21- a=(20 – 0)/(10 – 0)  —  a=2m/s²  —  d=área=5.10/2  —  d=25m  —  R- C

22- Considerando a área como sendo de um triângulo

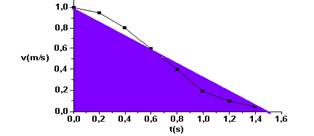
ΔS=b.h/=1,5.1,0/2  —  ΔS=0,75m  —  R- A

23- ΔS=área total=b.h + (B + b).h/2 + b.h=10.5 + (15 + 5).10/2 + 10.15=300m  —  ΔS=300m  —  V_m= ΔS/ Δt=300/30  —  V_m=10m/s

24- a) entre 0 e 20s  —  a=2m/s²  —  V_o=0  —  V₁= V_o + at=0 + 2.20  —  V₁=40m/s  —  entre 20s e 50s  —  V_o=40m/s  —  a=-1m/s²  —V₂=V_o + at=40 – 1.30  —  V₂=10m/s  —  gráfico abaixo

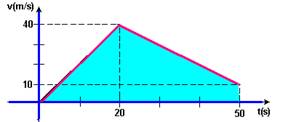
 b) ΔS=área=b.h/2 + (B _ b).h/2=20.40/2 + (40 + 10).30/2  —  A distância percorrida é 1150m.

25- T=4s  —  V=5 – 2.4  —  V=-3m/s  —  velocidade inicial – movimento progressivo, velocidade de -3m/s – movimento retrógrado  —  R- D

26- A distância percorrida corresponde à área compreendida entre a reta representativa  e o eixo do tempo, entre 0 e 3s, ou seja, à área de um trapézio  —  ΔS=área=(B + b).h/2=(80/3,6 + 40/3,6).3/2= (22,2 + 11,1).1,5  —  ΔS=49,95≈50m 

27- Observe atentamente que o único gráfico coerente com o enunciado é o da alternativa E  —  R- E

28- Quando t=0 eles estão na mesma posição (dado do exercício) —  quando t=4s, o deslocamento de cada carro é fornecido pela área

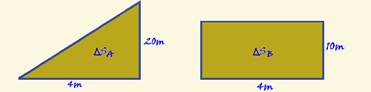
 entre 0 e 4s  —  carro A, a área é de um triângulo  —  ΔS_A=b.h/2=4.20/2  —  ΔS_A=40m  —  carro B, a área é de um retângulo  —  ΔS_B=b.h=4.10  —  ΔS_B=40m  —  R- A 

29-  Calculando o espaço percorrido pela área  —  ΔS_A=(B + b).h/2=(45 + 30).10/2  —  ΔS_A=375m  —  ΔS_B=(-10 – 30).10/2  — 

ΔS_B=-200m  —  d=375 + 200  —  d=575m  —  ou aceleração escalar de cada móvel, lembrando que  —  a_A=(45 – 30)/(10 – 0)  —  a_A=1,5m/s²  —  a_B=(-30 – (-10)/(10 – 0)  — 

a_B= -2m/s²  — S_A=S_oA + 30t + 0,75t²  —  S_B=S_oB – 10t – t²  —  supondo S_oA=0 e fazendo t=10s no encontro onde você iguala as equações  —  30(10) + 0,75(10)² = S_oB – 10(10) – (10)²  —  375 = S_oB – 200  —  S_oB = 575 m, que é a distância inicial entre os móveis, pois supusemos o móvel A partindo da origem.

R- A

30- Propriedade do gráfico v = f(t)  —   a área entre a linha do gráfico e o eixo t representa o espaço percorrido pelo móvel (DS)  —  como não há mudança de sentido, o espaço percorrido é igual à distância percorrida  —  R- D   

31-

R- A

32- a) V=V_o + at  —  80=0 + 2.t  —  t=40s

b) Na situação em que a pista tem o comprimento mínimo (d_m), o avião perde o contato com a pista exatamente em seu final  —    equação de Torricelli  —  v² – v_o² + 2.a.d_m  —  80²=0² + 2.2.d_m  —  6.400=4d_m  —  d_m=1.600m

33- Observe a figura abaixo  —  determinando a distância d por Pitágoras  —  (130)²=d² + (50)²  —  16.900=d² + 2.500  —  d=120m 

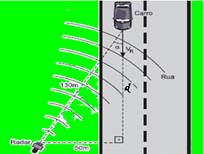
—  V_m=V_r.cosα  —  72=V_r.120/130  —  V_r=78km/h  —  R- C

 

34- Observe na figura abaixo onde a origem da trajetória foi colocada no ponto de partida do móvel A S_oA=0  —  a

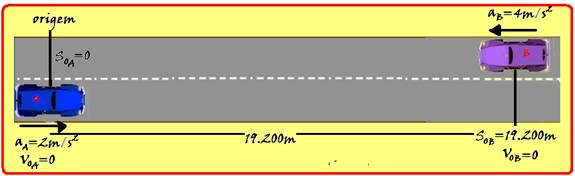
trajetória foi orientada para a direita S_oB=19200m  —  ambos os móveis partiram do repouso, V_oA=V_oB=0  —  como o móvel B está em movimento retrógrado e acelerado sua velocidade e sua aceleração são negativas (veja fisicaevestibular.com.br – mecânica – cinemática – gráficos do MUV)  —  dedução da função horária de cada móvel  —  S_A=S_oA + V_oAt + a_A.t²/2=0 + 0.t + 2t²/2  —  S_A=t²  —  S_B=S_oB + V_oBt + a_B.t²/2=19200 – 0.t – 4.t²/2  —  S_B=19200 – 2t²  —  no encontro AS=S_B  —  t²=19200 – 2t²  —  t²=6400  —  t=80s.

 

 

35-Colocando a origem das posições no instante inicial (t=0 e S_o=0) e deduzindo a equação de cada carro  —  S_A=V_ot + at²/2  —  S_B=2V_ot +(a/2).t²/2  —  S_B=2V_ot + at²/4  —  no encontro  —   S_A=S_B  —  V_ot + at²/2 = 2V_ot + at²/4  —  V_ot – 2V_ot + at²/2 – at²/4 = 0   — 

-4V_ot + at² = 0  —  t(at – 4V_o)=0  —  at – 4V_o=0  —  t=4V_o/a.

 

36-Observe na expressão D=K.V², onde K é constante e, nela você observa que a velocidade V é diretamente proporcional ao quadrado da velocidade  —  assim, se a velocidade dobra passando de 80kmh para 160kmh, a distância percorrida pelo carro até parar fica 2²=4 vezes maior  —  R- C

37- a) Falsa  —  a aceleração é positiva (concavidade para cima)  —  Entre 0 e t – o espaço decresce (movimento retrógrado, V<0)

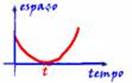
e o movimento é retardado, pois a e V tem sinais contrários (a>0 e V<0)  —  após t – o espaço cresce (movimento progressivo, V>0) e o movimento é acelerado, pois a e V tem mesmo sinal (a>0 e V>0)

b) Correta  —  como o movimento é retrógrado, a velocidade é negativa e, para que o movimento seja acelerado, a aceleração também tem que ser negativa, o que é o caso.

c) Falsa  —  o movimento é acelerado mas é progressivo (V>0).

d)  Falsa  —  se existe aceleração, o gráfico Sxt tem que ser uma parábola (equação do segundo grau).

R- B

 

38-  A área compreendida entre a reta representativa e o eixo dos tempos corresponde ao deslocamento ∆S do móvel no intervalo de tempo considerado  —  A e B (0 e t+Em todo gráfico da velocidade em função do tempo₁)  —  ∆S_AB=área do retângulo=b.h  —  ∆S_AB=V_ot₁  —  B e C (t₁ e t₂)  —  ∆S_BC=área do triângulo=b.h/2  — ∆S_BC=(t₂ – t₁).(V_o – 0)/2  —  ∆S_BC=V_o.(t₂ – t₁)/2  —  ∆S_BC/∆S_AB= [V_o.(t₂ – t₁)/2]/ V_ot₁  —  ∆S_BC/∆S_AB=(t₂ – t₁)/2t₁  —  R- C

 

39– Primeira situação  —  cálculo da aceleração do carro com a pista seca  —  V²=V_o² + 2.a.∆S  —  0² = 10² + 2.a.5  —  a=-10ms²  —  cálculo da aceleração do carro com a pista molhada  —  V²=V_o² + 2.a.∆S  —  0² = 10² + 2.a.6  —  a=-100/12=-25/3 ms²  —  Segunda situação  —  cálculo da distância percorrida com a pista seca  —  V²=V_o² + 2.a.∆S  —  0² = 30² + 2.(-10). ∆S  —  ∆S =45m  —  cálculo da distância percorrida com a pista molhada  —  V²=V_o²+ 2.a.∆S  —  0² = 30² + 2.(-25/3).∆S  —  ∆S=54m  —  distância a mais  —  d=54 – 45=9m  —  R- D

Voltar para os Exercícios