Movimento Circular – Resolução

Resolução comentada dos exercícios de vestibulares sobre MOVIMENTO CIRCULAR

 

01- T=30s  —  f=1/T=1/30  —f=1/30Hz  —  f=(1/30).60  — f=2rpm

02- T=6s  —  f=1/3Hz

03- f=1/1h=1/3.600Hz  —  T= 3.600s  —  R- A

04- Terra – volta completa em 24h  —  T_T=24h  —  f’=1/24rph(rotações por hora)  —  relógio – ponteiro das horas – volta completa em 12h  —  f=1/12rph  —  f/f’=(1/12).(1/24)  —  f/f’=2

05- O tempo em que a Lua demora para dar uma volta em torno da Terra (período de translação da Lua em torno da Terra), é o mesmo que ela demora para sofrer rotação em torno de si mesma (período de rotação da Lua)  —  R- C

06- 20 voltas – 10s  —  1 volta – T  —  T=0,5s  —  f=1/T=2Hz  — R- A

07- W=2π/T  —  como as grandezas 2π e T são constantes, W também será  —  R- D

08- Observe que cada ponto da periferia das rodas da frente e de trás, possuem a mesma velocidade que a do trator, ou seja, V_f=V_t=V.

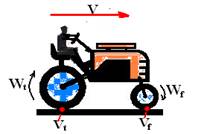
Mas, possuem velocidades angulares diferentes, pois W=2π/R e assim, W é inversamente proporcional a R, e como o raio da roda da frente é menor, ela gira mais que a maior tendo maior velocidade angular que a mesma  —  W_f > W_t   —  R- D

09- a) T=1/f=1/10  —  T=0,1s  —  esse é o tempo que qualquer ponto da polia demora para efetuar uma volta completa.

b) W_A=W_B=2π/T=2π/0,1  —  W_A=W_B=20π rad/s

c) V_A=2πR_A/T=2π0,5/0,1  —  V_A=10π m/s  —  V_B=2πR_B/T=2π.1/0,1  —  V_B= 20π m/s  (observe que V_B > V_A, pois está mais afastado do centro 0)

10- Observe a figura abaixo:

I- falsa  —  o ponto B está mais afastado do centro e V_B > V_A

II- correta  —  descrevem o mesmo ângulo no mesmo tempo

III- correta  —  demoram o mesmo tempo para efetuar uma volta completa

R- E

11- As velocidades escalares das periferias das rodas das bicicletas do pai e do filho são as mesmas  —  V_p=V_f  —  f_pR_p=f_fR_f   — 

R_p=2R_f  —  f_p.2R_f=f_fR_f  —  f_p=f_f/2  —  R- A

12- a) 30 voltas ou 60 voltas ou 90 voltas, ou seja, 30.n voltas, com n natural não nulo.

b) menor W  —  menor f  —  f=30Hz  —  W=2π/T=2πf=2.3.30  —  W=180 rad/s

c) W=V/R  —  180=V/0,3  —  V=54m/s

13- V=0,2=2.10^-1m/s  —  R=0,8/2  —  R=0,4mm=0,4.10^-3  —  R=4.10^-4 m  —  W=V/R=2.10^-1/4.10^-4  —  W=0,5.10³ rad/s  —  W=500 rad/s  —  R- E
14- R- D – (veja teoria)

15- Veja na expressão W=V/R, que W é constante (o eixo do carro gira com a mesma velocidade angular) e, assim, V é diretamente proporcional a R  —  como o diâmetro e consequentemente o raio teve um aumento de 10%, a velocidade também deverá ter o mesmo aumento, passando de 100km/h para 110km/h  —  R- C

16- a) 16 cubas x 5L=80L  —  como a vazão é de 160L/min, em 1 min a roda efetua 2 voltas  —  f=2rpm x 60  —  f=1/30 Hz  —  T=1/f  —  T=30s

b) regra de três  —  160 L – 1 min  —  X L  – 60min  —  X=9.600L

17- Velocidade de qualquer ponto da linha do equador (inclusive Macapá), após uma volta completa da Terra (T=24h)  —  V=ΔS/T=40.000/24  —  V=10.000/6km/h  —  com essa velocidade, no tempo que a estação demora para efetuar uma volta completa (Δt=90min=1,5h), Macapá  percorreu uma distância de V= ΔS/Δt  —  10.000/6= ΔS/1,5  —  ΔS=2.500km  —  R- D

18- Nos pontos de contato entre a prancha e os pontos da periferia de cada polia, a velocidade tangencial é a mesma tendo, em cada polia, o sentido em que a prancha está se movendo  —  R- C

19- Num relógio sem defeitos o ponteiro dos minutos ao efetuar um volta completa (60min) efetua um ângulo de 2πrad  —  no relógio defeituoso, ao efetuar uma volta completa (50min) ele efetuará um ângulo θrad  —  regra de três  —  60min – 2πrad  —  50min – θrad  —  θ=100π/60  —  θ=5π/3 rad  —  o relógio sem defeitos medirá esse ângulo sendo efetuado em 1h=3.600s  —W=Δθ/Δt=

=(5π/3)/3.600  —  W=π/2160  —  R- A

20- V=150m/min  —  W=V/R=150/5  —  W=30rad/min  —  R- D

21- R=6.400 + 5.298  —  R=11.698km  —  comprimento da órbita  —  ΔS=2πR=2.3.11.698  —  ΔS=70.188km  —  velocidade escalar do satélite  —  V=5.849m/s  —  V= ΔS/Δt  —  5.849=70.188/Δt  —  Δt=12.000s/3.600  —  Δt=3,33h  —  e um dia ele efetua 24/3,33=7,2 voltas completas  —  como em cada volta completa ele passa duas vezes pela linha do equador, ele efetuará 2.7,2=14,4 passagens  —  14 passagens completas

22- R=6.400 + 400=6.800km  —  em Δt=6,8πh ele percorreu  —  ΔS=V. Δt=26.000.6,8π  —  ΔS=176.800π km  —  para efetuar uma volta completa ele percorre l=2πR=2π.6.800  —  l=13.600π km  —  regra de três  —  1volta – 13.600π km  —  n voltas – 176.800 km  —  n=176.800/13.600  —  n=13 voltas  —  R- C

23- a) Para atravessar o cilindro a bala percorreu d=3m com velocidade de V=600m/s  —  V=d/t  —  600=3/t  —  t=0,005s

b) Observe a figura abaixo

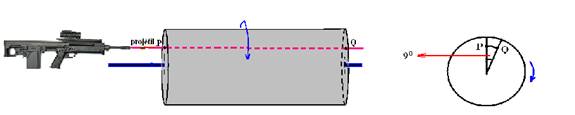
Em t=0,005s o cilindro girou de 9^o  —  regra de três  —  π rad – 180^o  —  θ rad  —  9^o  —  θ=9π/180  —  θ= π/20 rad  — 

W=θ/t=(π/20)/0,005  —  W=10π rad/s  —  W=2π/T  —  10π=2π/T  —  T=1/5s  —  f=1/T  —  f=5 Hz

24- f=4.50- rpm=4.500/60  —  f=75Hz  —  W=2πf=2.3.75  —  W=450 rad/s  —  W=V/R  —  450=V/0,3  —  V=135ms ou V=135 x 3,6  —  V=486km/h

25- Freqüência das balas=30 balas por minuto que deve ser a mesma de rotação do disco  —  f_o=30rpm ou f₁=60rpm, ou f₂=90rpm e assim por diante.

26- Observe a figura abaixo:

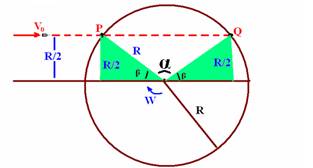
senβ=(R/2)/R  —  senβ=1/2  —  β=30^o  —  observe que para ir de P para Q ele “varreu” um ângulo α=120^o =2π/3 —  α=2π/3 rad  —  W=α/t  —  2π=(2π/3)/t  —  t=1/3s  —  observe que a distância horizontal PQ vale  —  PQ=Rcos30^o + Rcos30^o=2R√3/2=

=2.0,5.√3/2  —  PQ=√3/2m  —  V_o=ΔS/Δt=PQ/t=(√3/2)/(1/3)  —  V_o=√3/2 x 3/1  — V_o=3√3/2m/s ou V_o≈2,6m/s

27- As voltas que faltam para terminar a prova, 25 para o piloto A e 26 para o piloto B devem ser completadas ao mesmo tempo  — 

Sendo X o comprimento da pista, o piloto A deverá percorrer ΔS_A=25.X e o piloto B, ΔS_B=26.X no mesmo tempo t, com velocidades respectivamente iguais a V_A e V_B  —  V_A= ΔS_A/t  —  t=25.X/V_A (I) —  V_B= ΔS_B/t  —  t=26.X/V_B (II)  — 

Igualando I com II  —  25X/V_A=26X/V_B  —  V_B/V_A=26/25=1,04

28- Em um corpo em rotação:

Em um corpo em rotação todos os pontos apresentam mesmo período (T), freqüência (f) e velocidade angular (ω), que são os mesmos que da Terra.. Logo: T_Macapá  = T_{São Paulo} = T_Selekhard  —   f_Macapá = f_{São Paulo} = f_Selekhard  —  W_Macapá=W_{São Paulo}=W _Selekhard  —   A velocidade escalar de um ponto é dado pela expressão v = ω ⋅ r.

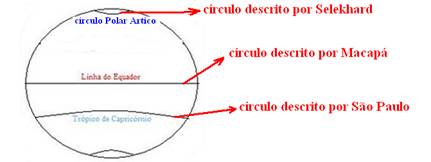
 Logo, sendo a velocidade angular será a mesma para todos os pontos, a velocidade escalar (intensidade da tangencial) será maior quanto maior for o raio (r) em relação ao eixo de rotação. Portanto: V_Macapá > V_{São Paulo} > _ V_Selekhard  —  R- A

29- Próximo ao centro  —  R=20mm=20.10^-3  —  R=2.10^-2m  —  W=V/R  —  uma volta completa  —  W=2π/T=2πf  —  V/R=2πf  —  1,26/2.10^-2=6,3f  —  f=10Hz x 60  — f=600rpm

Próximo à beirada  —  R=60mm=60.10^-3  —  R=6.10^-2m  —  W=V/R  —  uma volta completa  —  W=2π/T=2πf  —  V/R=2πf  —  1,26/6.10^-2=6,3f  —  f=1/30Hz x 60  — f=200rpm  —  R- A

30- Velocidade angular do tambor antes de descarregar  —  W_a=2πf_a=2π4  —  W_a=8π rad/min  —  ao descarrega W_d=5W_a=5.8π  — 

W_d=40π rad/min  —  freqüência ao descarregar  —  W_d=2πf_d  —  40π=2πf_d  —  f_d=20 rad/min  —  f_dR_d=f_menor.R_menor —  20.0,6=f_menor.0,2   —  f_menor=60 rpm  —  R- E

31- Como as rodas giram acopladas cada ponto da periferia de cada uma delas possui a mesma velocidade linear (escalar) V_A=V_B=V_C  —  para cada roda o número de dentes é diretamente proporcional ao comprimento de cada circunferência, que por sua vez é diretamente proporcional a cada raio  —  R_A/32=R_B/64=R_C/92  —  R_A=R_B/2=R_C/3  —  R_A=R_C/3=12/3  —  R_A=4 cm  —  R_B=8cm  —  R_A=4cm  —  R_B=8cm e R_C  —  R_C=12cm  —  W_C=V_C/R_C  —  6=V_C/12  —  V_C=72 cm/s=V_A=V_B  —  W_A=V_A/R_A  —  W_A=72/4  —  W_A=18 rad/s  —  R- C

32- As duas polias menores têm a mesma velocidade dada por V=ΔS/Δt=0,6/5  —  V=0,12m/s  —  freqüência de rotação das polias menores  —  V=2πfR  —  0,12=2.3.f.3.10^-2  —  f=2/3Hz  —  A polia maior e as menores tem a mesma freqüência (acopladas pelo mesmo eixo)  —  relação entre a polia maior e a que está acoplada à ela  —  f₁R₁=f₂R₂  —  f₁.3.10^-2=2/3.18.10^-2  —  f₁=4Hz  —  R- D

33- A luz estroboscópica tem freqüência de 5Hz, ou seja, ilumina o pneu a cada T=1/f=1/5=0,2s  —  assim, se a roda girasse ele com freqüência de 5Hz, ele veria a mancha branca sempre na mesma posição (a mancha daria uma volta completa a cada 0,2s)  —  mas como ele vê a mancha como se o carro se movesse para trás, a mancha deve demorar menos que 0,2s para dar uma volta completa, assim  —  T < 0,2s  —  1/f < 0,2  1/f <1/5  —  f < 5Hz  —  R- B  

34- Observe que entre o primeiro e o segundo pentagrama a pá de cor diferente girou 3π/2 rad em t=1/24s  —  num período T ela gira 2π rad  —  regra de três  —  3π/2 rad – t=1/24 s  —  2π rad – T s  —  3πT/2=2π/24  —  T=4/72  —  T=1/18s  —  f=1/T  —  f=18Hz  —  R- B

35- a) T=0,5min=30s  —  f=1/T=1/30  —  f=1/30 Hz

b) W_e=2π/30  —  W_e=π/15 rad/s  — V_e=V_m=W_eR_e=(π/15).4  —  V_e=V_m=4π/15 cm/s  —  W_m=V_m/R_m = 4π/15.1 —  W_m=4π/15 rad/s  —  W_m/W_e=4π/15 x π/15  — W_m/W=4

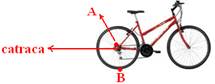
36- a) Observe a figura abaixo:

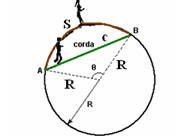
 Considerando θ em rad  —  velocidade de Maria  —  S=tamanho do arco  AB  —    θ=S/R  —  S=R. θ  —   V_y=S/R=R. θ/t  —  V_y=R θ/t  —   velocidade de João  —  c=comprimento da corda AB  —  lei dos cossenos  —  c²=R² + R² – 2.R.R.cos θ  —  c²=2R² – 2R²cos θ  —  c²=2R²(1-cos θ)  —  c=√(2R²(1 – cos θ)  —  c=R.√(2 – 2cos θ)  —  V_x=c/t=R.√(2 – 2cos θ)/t  —  V_x/V_y=

=R.√(2 – 2cos θ)/t x t/(R θ)  —  V_x/V_y=√(2 – 2cos θ)/θ

b) θ=60^o  —  θ=π/3 dad  —  V_x/V_y=√(2 – 2cos θ)/θ  —  V_x/V_y=√(2 – 2cos π/3)/π/3  —  V_x/V_y=√(2 – 2.1/2)/(π/3)  — 

V_x/V_y=1/π/3  —  V_x/V_y=3/π

37- Comparando φ = π/4 + π/2.t com φ = φ_o + W.t  

a) φ_o=π/4 rad   

b) W=π/2 rad/s

c) t=8s  —  φ = π/4 + π/2.t  —  φ = π/4 + π/2.8  —  φ = π/4 + 4π  —  φ = 17π/4 rad —   como a cada volta ele efetua 2π rad  — 

n=(17π/4)/2π  —  n=8,5 voltas

d) Multiplicando cada membro da expressão φ = π/4 + π/2.t  pelo raio R=4m  —  φ.4 = (π/4).4 + (π/2).4.t  —  S= π + 2πt

38- Parando o corredor B, o A estará se afastando dele com velocidade relativa de V_R=8 – 6=2m/s e para ficar com uma volta de vantagem sobre ele deverá a distância correspondente a uma volta completa d=2πR=2.3.12,0=72,0m  —  V_R=d/t  —  2=72,0/t  —  t=36, 0s  —  ou, na forma angular  —  φ_A=V_A/R=8/12,0=1/1,5 rad/s  —  φ_B=V_B/R=6/12,0=1/2 rad/s  —  velocidade angular relativa  —  W_R=W_A – W_B=1/1,5 – 1/2  —  W_R=1/6 rad/s  —  W_R=Δφ/Δt  —  1/6=2π/t  —1/6=2.3/t  —  t=36,0s  —  ou ainda  —  φ_A= φ_o + W_A.t=0 + 1/1,5.t  —  φ_A= 1/1,5.t  —  φ_B= φ_o + W_B.t=0 + 1/2.t  —  φ_B= 1/2.t  —  φ_A – φ_B=2π  —-  1/1,5t – 1/2t = 2π  —  t=36,0s  

39- a) S_A =S_o + V_A.t  —  S_A = 0 + 8.20  —  S_A = 160m  —  S_B =S_o + V_B.t  —  S_B = 0 + 6.20  —  S_B=120m  —  ΔS=160 – 120  —  ΔS=40m

b) Parando o corredor B, o A estará se afastando dele com velocidade relativa de V_R=8 – 6=2m/s e para ficar com uma volta de vantagem sobre ele deverá a distância correspondente a uma volta completa d=120m  —  V_R=d/t  —  2=120/t  — t=60s

40- a) W_A=2π/T=2π/6  —  W_A= π/3rad/s  —  para retornar a P, A “varreu” um ângulo de Δφ=2π rad  —  W_A=2π/t  —  π/3=2πt  —  t_A=6s  —  para retornar a P, B  “varreu” um ângulo de Δφ=2π rad  —  W_B=2π/t  —  π/6=2πt  —  t_A=12s  —  assim, eles se encontram em 12s, quando B deu uma volta e A, duas; em 24s quando o móvel B deu duas voltas e o móvel A quatro, e assim por diante.  

b) Como eles se movem em sentidos contrários a velocidade relativa é a soma das velocidades  —  W_R=W_A + W_B=π/3 + π/6  —

W_R=π/2 rad/s  —  um deles pára e o outro se desloca com W_R=π/2 rad/s e percorre até o encontro Δφ=2π rad  —  W_R=2π/t  —  π/2=2π/t t=4s  —  se encontram de 4s em 4s.

41- A primeira partícula efetua 1/3 rpm o que corresponde  a 15 voltas por hora, enquanto que a segunda faz 20 voltas por hora.

Do ponto de vista de uma das partículas a outra executa 35 voltas por hora. Assim elas se encontram 35 vezes em uma hora.

42- A partícula mais lenta B, demora 15s para efetuar uma volta completa e passar pelo ponto de partida, enquanto que a A, 10s  —   elas vão se encontrar novamente no ponto de partida no instante t=30s, quando a B deu 2 voltas e a A 3 voltas  —  R- E

43- Mesmo sentido (t=30s)  —  φ_B – φ_A=2π  —  (2π/T_B)t – (2π/T_A)t=2π  —  1/T_B – 1/T_A=1/30 (I)  —  sentidos opostos (t=10s)  —  φ_B + φ_A=2π  —  (2π/T_B)t + (2π/T_A)t=2π  —  1/T_B + 1/T_A=1/10 (II)  —  resolvendo (I) com (II)  —  T_A=15s e T_B=30s

44- a) A_t e λ são nulos  —  MCU

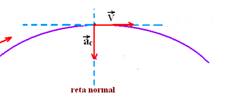
b) T=10s  —  f=1/10 Hz  —  W=2π/T  —  W=2π.1/10  —  w = π/5 rad/s  —  W=V/R — π/5=V/2  —  V=2π/5 m/s  —  a = a_c= v²/r  —  a = (2π/5)²/R  —  a = 4π²/50  —  a = 2π²/25 m/s²

45-

a_t=a=1m/s²  —  V=V_o – at=0 – 1.2  —  V=-2m/s²  —  a_c=V²/R=4/1  —  a_c=4m/s²  —  λ²=1² + 4²  —  λ=√17 m/s²

46- O período de rotação da manivela é T= 30s e a sua frequência de rotação vale f=1/30Hz  — essa freqüência da manivela é a mesma que a da engrenagem menor  —  essas engrenagens estão em contato e o raio da engrenagem é proporcional (constante K) ao número de dentes  —  f₁.r₁=f₂.r₂  — 1/30.10K=f₂.24K  —  f₂=1/72 Hz  —  a velocidade escalar da vara de cana é a mesma que a da periferia da roda 2, que é a mesma que de cada cilindro de raio 4cm  —  V=2π.f.r₂=2.3.1/72.4  —  V=1/3cm/s=0,33cm/s  — 

R- B  

47- T=60min  —  V=2πR/T=2.3.1/60  —  V=0,1cm/s  —  R- A

48- V=2πR/T=2.3.36.10³/3.600 x 24  —  V=216.10³/86.400  —  V=2,5km/s  —  R- C

49- Cada pá efetua 3 voltas por segundo x 3 pás=9 voltas por segundo  —  —  f=9Hz  —  T=1/9s  — esse é o tempo que cada pá demora para dar uma volta completa, deixando passar luz (gerando pulsos) metade desse tempo  —  T=(1/9)/2  —  T=1/18s  —  cada pulso demora o inverso de 18s  —  R- D

50- Quando B partiu, A já havia efetuado, em t=4s, com W_A= 1,5 rad/s  —  φ=W.t=1,5.4  —  φ=6 rad  —  fazendo os dois partirem juntos com φ_oA=6rad e φ_oB=0  —  equação de A  —  φ_A= φ_oA + W_A.t  —   φ_A= 6 + 1,5.t  —  equação de B  —  φ_B= φ_oB + W_B.t  — 

φ_B= 0 + 3.t  —  quando se encontram pela primeira vez, B está uma volta completa (2πrad) na frente de A  —  φ_{B –} φ_A=2π  — 

3t – 6 – 1,5t=2π  —  1,5t=2π + 6  —  t=12/1,5  —  t=8s   

51- V=240.000km/s=24.10⁴km/s=24.10⁷m/s  —  t=1h=3.600s=36.10²s  —  V=d/t  —  24.10⁷=d/36.10²  —  d=864.10⁹m  —  regra de três  —  1 volta – 27.10³m  —  n voltas – 864.10⁹ m  —  n=864.10⁹/27.10³  —  n=32.10⁶=32.000.000 voltas

52- a) Velocidade escalar V=2,4m/s da periferia da roda d’água de raio R, que gira com freqüência f=0,20Hz  —  V=2πRf  —  2,4=2.3.R.0,20  —  R=2,0m 

b) A diferença de massa (Δm) entre os produtos e os reagentes da reação química de fissão é transformada em energia e essa diferença vale  —   Δm=m_reagentes – m_produtos=1.004 – 1.003=1g  —  Δm=1g=10^-3kg  —  E=√Δm.c²  —  E=10^-3.(3.10⁸)²=10^-3.9.10¹⁶  —  E=9.10¹³J

53- Dados: R = 6 cm = 6.10^-2 m; f = 0,25 Hz; π= 3,1.

v = 2 p R ­f = 2 (3,1) (6.10^-2) (0,25)  —  v = 9,3.10^-2 m/s.

R- E

54- Observe na figura abaixo que a segunda e última foto são idênticas (repetidas), e que entre elas o cavalo percorreu 15m  —

  ΔS=15m   —  o período (T) do movimento é o tempo decorrido entre duas repetições  —  freqüência  —  f=0,5Hz  — T=1/f  —  T=1/0,5  —  T=2s  —  V=ΔS/Δt= ΔS/T=15/2  —  V=7,5m/s  —  R- B

55- Observe que nos trechos retos as distâncias percorridas pelos atletas das partes interna e externa é a mesma  —  o acréscimo é devido apenas à distância devida ao trecho externo de raio R=8m   —  ΔS=πR + πR=2πR=2.3,14.8  —  ΔS=50,24m  — 

R- D

56- Observe que, em cada volta completa, quanto maior a área de contato da sapata com as rodas, maior será o atrito que fará parar a bicicleta e consequentemente menor será o tempo de parada  —  R-E

57- A figura abaixo representa as trajetórias das duas rodas da bicicleta após ela percorrer uma volta completa:

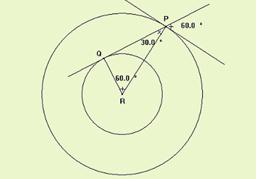
O triângulo PQR é retângulo, e os segmentos RQ e RP são os raios dos círculos descritos, respectivamente, pela roda traseira e pela roda dianteira  —  como se pode observar na figura, o ângulo QPR mede 30^o  —  portanto  —  RP=2RQ  — a distância percorrida pela roda traseira em uma volta da bicicleta é igual a  —  2π(RQ)  —  o número de voltas dadas por essa roda em torno de seu eixo para percorrer essa distância é igual a  —  N₁=2π(RQ)/ 2πR_t  —  N₁=RQ/R_t  —  onde R_t é o raio da roda traseira  —   a distância percorrida pela roda dianteira é igual a  —  2π(RP)  —  o número de voltas dadas por essa roda em torno de seu eixo para percorrer essa distância é igual vale  —  N₂=2π√(RQ)/ 2πR_d  —  R_d  —  raio da roda dianteira  —  R_d=2R_t  —  RP=2RQ  —
N₁/N₂=(RQ/R_t)/(RP/R_d)=RQ/R_t x R_d/R_p= RQ/R_t x R_d/R_p=(RQx2R_t)/R_tx2RQ  —  N₁/N₂=1  —  R- A
58- Período T do ponteiro dos segundos  —  T=60s  —  ΔS=2πR=2.3,14.96  —  ΔS=602,88m  —  R- B

59-

R- D

60- A distância d deve ser igual ao comprimento de cada circunferência das rodas vezes um número inteiro de voltas, para que os pontos A e B estejam simultaneamente  em contato com o solo. Assim, supondo que a distância d será atingida após a roda menor dar um número x de voltas e a roda maior um número y de voltas, tem-se  —  d = x . 2 . π . 27 e d = y . 2 . π . 33  —  igualando  —  x . 2 . π . 27 = y . 2 . π . 33  —  9 . x = 11 . y  —  como x e y devem ser números inteiros e 11 é um número primo, então x = 11 e y = 9  —  assim, d = 11 . 2 . π . 27 = 594 π cm,    ou    d = 9 . 2 . π . 33 = 594 π cm  —  como a resposta está em metros  — 

d = 5,94 π m  —  R- C

 

61-

-(V) Verdadeira  —  todos os pontos da correia tem a mesma velocidade linear (escalar) que todos os pontos da periferia (parte externa) da catraca e que todos os pontos da periferia da coroa  —  estão unidos pela mesma correia.

(V) Verdadeira  —   um ponto da periferia da roda  terá maior velocidade (escalar, linear) V=ΔS/Δt, pois deverá percorrer maior distância ΔS para, no mesmo intervalo de tempo, poder acompanhar um ponto da periferia da catraca, ou seja,V_roda>V_catraca.  

(V) Verdadeira  —  observe que o raio da catraca é menor que o da coroa, e ela deve girar mais (“varrer” um ângulo maior) que a coroa no mesmo intervalo de tempo  —  na expressão da velocidade angular (W= Δφ/Δt), como ∆t é o mesmo e Δφ da catraca é maior, esta deve ter velocidade angular maior que a da coroa.

 (V) Verdadeira  —  observe que, como “varrem” o mesmo ângulo (Δφ) no mesmo intervalo de tempo, suas velocidades angulares (W= Δφ/Δt) serão iguais.

R- C

62-

Observe os respectivos raios de cada roda na figura abaixo  —  o pneu ao efetuar uma volta completa percorre em ∆t=1s  —

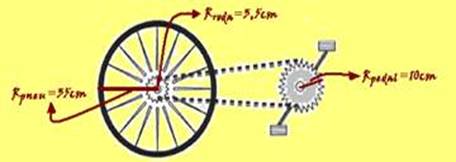
∆S=2πR_pneu=2.3.35  —  ∆S=210cm  —  cálculo do tempo (período T) que o pneu demora para percorrer essa distância (uma volta completa) com velocidade de 5m/s  —  V=∆S/∆t=∆S/T  —  5=2,1/T  —  T=0,42s  —  frequência do pneu  —  f=1/T=1/0,42  —

f_pneu=2,4 Hz (voltas por segundo)  —  observe que essa frequência é a mesma que a da roda acoplada ao pneu  —  f_roda=2,4Hz  —

as duas rodas dentadas, presas por corrente, possuem a mesma velocidade escalar (linear e obedecem à relação  —  f_roda.R_roda =

f_pedal.R_pedal  —  2,4.3,5 = f_pedal.10  —  f_pedal=0,84Hz (rps) —  f_pedal=0,84×60=50,4rpm  —  R- E

63-

A efetua uma volta completa percorrendo a distância d em 80s  —  VA=d/80  —  B efetua 90% de uma volta completa (0,9d) em 80s  —VB=0,9d/80  —  colocando a origem das trajetórias no ponto de partida de A e considerando o movimento no sentido

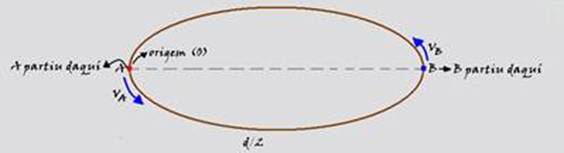
horário  —  SoA = 0, SoB=d/2  —  equação horária de A  —  SA=SoA + VA..t= 0 + (d/80).t  —  SA=(d/80).t  —  SB=SoB + VB.t=d/2 + (0,9d/80).t  —  no encontro eles ocupam a mesma posição  —  SA=SB  —  (d/80).t = d/2 + (0,9d/80).t  —  (0,1.d.t)80 = d/2  —  0,1t=40  —  t=400s=6min40s  —R- E

64-

-01. Correta  —  essa é a definição de período de um MCU.

02. Correta  —  essa é a definição de frequência de um MCU.

04. Correta  —  numa volta completa  —  ∆S=2.π.R  —  observe que o raio R é diretamente proporcional á distância percorrida.

08. Correta  —  além disso ela tem direção radial, sentido para o centro da circunferência e intensidade F_c=m.a_c=m.V²/R.

16. Falsa  —  a_c=V²/R  —  observem que a_c e R são inversamente proporcionais.

Corretas: 01, 02, 04 e 08  —  Soma=15.

65-

Pelo enunciado, enquanto a roda maior percorre ∆SR=(2/3).2πR, a roda menor percorre uma volta completa  —  ∆Sr=2πr  —  como a correia é inextensível e não desliza a velocidade escalar (linear) de qualquer ponto da correia é a mesma que a de qualquer pontos da periferia de cada roda  —  VR=∆SR/T  —  Vr=∆Sr/T  —  VR = Vr  —  (2/3).2πR/T = 2πr/T  —  2R/3 = r  —  R/r=3/2  —  R- C

 

Voltar para os Exercícios