Lançamento oblíquo – Resolução dos exercícios de vestibulares

Resolução dos exercícios de vestibulares sobre lançamento oblíquo

 

01- O tempo que a bola permanece no ar está relacionado  com a altura  —  maior altura, maior tempo de permanência no ar  —  R- A

02- I – Falsa – a aceleração é constante e é a aceleração da gravidade , sempre com direção vertical e sentido para baixo.

II – Correta – vide afirmação acima

III – Falsa – no ponto mais alto da trajetória a velocidade é mínima e vale V=V_x

R- C

03- Se os dois ângulos de lançamento forem complementares entre si (α₁ + α₂=90^o), e a velocidade inicial for a mesma, (no caso, 20m/so alcance horizontal é o mesmo.

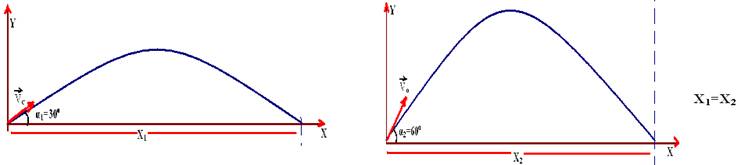
R- D

04- a) Como a resistência do ar é desprezada, a velocidade horizontal inicial do projétil é constante e, em cada instante, a mesma do caminhão. Assim, se ele partiu de um ponto P da carroceria do caminhão, retornará ao mesmo ponto P e o deslocamento horizontal em relação ao caminhão será zero.

b) V_ox=20m/s  —  V_o=80m/s  —  V_o²=V_ox² + V_oy²  —  6.400=400 + V_oy²  —  V_oy=77.5m/s  —tempo de subida  —  V_y = V_oy – gt_s  —  0=77,5 – 10t_s  —  t_s=7,75s  —  tempo que demora para subir e descer e se deslocar X na horizontal  —  t=2.7.75  —  t=15,5s  —  X=V_ox.t=20,15,5  —  X=310m

05- (01) Falsa – é o tempo de subida mais o tempo de descida

(02) Verdadeira – veja (1)

(04) Verdadeira – veja teoria – Se a altura maxima (h_máx) é igual ao alcance X  —   tgα=4

(08) E_c=mV²/2  —  na altura máxima V é mínima, portanto E_c também será mínima – Falsa

(16) Falsa – como não existe atrito, o sistema é conservativo e a energia mecânica é sempre a mesma em todos os pontos da trajetória

Soma (02 + 04) = 06

06- Na altura máxima a velocidade vetorial  não é nula, tem intensidade mínima e é igual à componente horizontal, ou seja, .

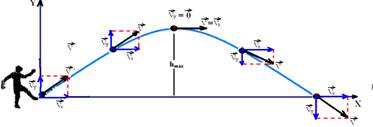
Assim, V_ox=20m/s  —  V_ox=V_ocos60^o  —  20=V_o.1/2  —  V_o=40m/s  —  R- E

07- Na altura maxima  —  h_máx=20m e t=4/2  —  t=2s  —  Y=V_oyt – gt²/2  —  20=V_oy.2 – 10.2²/2  —  V_oy=20m/s  —  Y=V_oyt – gt²/2  —  Y=20t – 5t²   —  R- A

08- No ponto mais alto  —  V=V_x=V_ox=20/2  —  V_ox=10m/s  —  V_o²=V_ox² + V_oy²  —  20²=10² + V_oy²  —  V_oy²=300  —  na altura máxima h_máx  —  V_y=0  —  Torricelli  —  V_y² = V_oy² – 2gh_máx  —  0²=300 – 20h_máqx  —  h_máx=15m

09- a) Movimento na vertical  —  no ponto A de altura máxima V_y=0 

S=S_o + V_ot + at²/2  —  YB) = Y(A) + V_yt – 10t²/2  —  4,2 = 5,0 +0.t -5t²  —  t=√0,16  —  t=0,4s
b) Queda livre da altura Y_o=5m  — V_o=0  —  quando chega ao solo Y=0  —  Y=Y_o + V_ot –gt²/2  —  0=5 + 0t – 5t²  —  t=1s

Sendo o choque elástico, o tempo de subida é igual ao tempo de descida  —  t=2s

c) Movimento vertical  —  a batida na parede não afeta o tempo de queda (projeção na vertical) pois o choque é elástico —  t=1s  —  V_oy=0  —  velocidade com que chega ao solo  —  V_y  —  V_y=V_oy – gt  —  V_y=0 -10.1  —  V_y=-10m/s  —  se chega ao solo com velocidade de -10m/s, sai do mesmo com velocidade de +10m/s  —

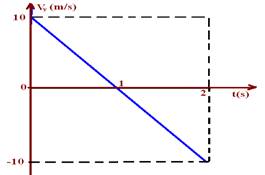
No movimento horizontal ela demora t=0,4s para percorrer X=6m com velocidade constante V_x  —  X=V_xt  —  6=V_x.0,4  —  V_x=15m/s  —  +15m/s para a direita (movimento progressivo) e -15m/s para a esquerda (movimento retrógrado)

 

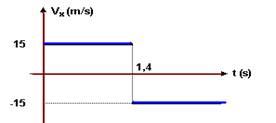
10- V_ox=V_ocos45^o  —  V_oy=V_osen45^o  —  V_ox=V_oy=0,7V_o  —  tempo que o dardo demora para para percorrer 16m na horizontal  —  X=V_oxcos45^o.t  —  16=V_o.0,7.t  —  t=16/0,7V_o  —  Na altura máxima V_y=0 e t=16/2.(0,7V_o)=16/1,4V_o  —  V_y=V­_oy – gt  —  0=0,7V_o – 10t  —  0=0,7V_o – 10.16/1,4V_o  —  V_o=√163,2=12,8m/s  —  t=16/0,7V_o  —  t=16/12,8=1,8s  —  R- B

11- a) A única força que age sobre a bola (a resistência do ar é desprezada) durante todo o movimento é a força peso, vertical e para

baixo.

b) Cálculo do tempo que a bola demora  a chegar até o goleiro percorrendo X=40m com velocidade horizontal constante e de valor V_ox=V_ocos25^o=26.0,91  —  V_ox=23,66m/s  —  X=V_ox.t  —  40=23,66.t  —  t=1,69s  —  cálculo da altura, na direção vertical, que a bola estará ao chegar ao goleiro nesse instante (t=1,69s)  —  Y=V_oyt – gt²/2  —  Y=V_o.sen25^o.t –gt²/2  —  Y=26.0,42.1,69 – 10.(1,69)²/2  —  Y=18,45 – 14,28  —  Y=4,17m  —  esse valor é maior que 3m e assim, o goleiro não consegue tocar a bola.

c) Cálculo do tempo que a bola demora para chegar à altura vertical de 1,5m  —  Y=V_o.sen25^o.t – gt²/2  —  1,5=10,92t – 5t²  —

5t² -10,92t + 1,5=0  —  Δ=119,25 – 30=89,25  —  √Δ=9,5  —  t=(10,92 ±9,5)/2.5  —  considera-se o tempo maior que ocorre quando a bola já está descendo  —  t=2,042s  —  nesse instante a distância horizontal da linha de gol será de X=V_ocos25^o.t  — 

X=26.0,91.2,042  —  X=48,3m

12- O tempo que a gota de barro permanece no ar é o mesmo tempo que a roda demora para efetuar uma volta completa, ou seja, percorrer ΔS=2πR com velocidade constante V, que é a velocidade de translação e de rotação da roda (não derrapa) e que também é a velocidade de lançamento da gota de barro  —  V= ΔS/Δt  —  V=2πR/t  —  t=2πR/V  —  a gota de barro atinge a altura máxima h_máx na metade desse tempo, quando sua velocidade vertical V_y se anula (V_y=0)  —  V_y=V_oy – gt  —  0=V – g(πR/V)  — 

V²=πRg  —  V=√(πRg)

13- a) Do gráfico  —  distância vertical que percorre  até atingir a altura máxima  —  ΔS=125 – 93,75=31,25cm  —  ΔS=0,3125m  —  na altura máxima V_y=0  —  Torricelli  —  V­_y² = V_oy² + 2aΔS  —  0²=V_oy² – 2.10.0,3125  —  V_oy=2,5m/s  —  função horária vertical  —  Y=Y_o + V_oyt – gt²/2  —  quando chega ao solo Y=0  —  0=0,9375 + 2,5t – 5t²  —  5t² – 2,5t – 0,9375=0  —  √Δ=5  — 

t=(2,5 ±5)/10  —  t=0,75s

b) Na horizontal  —  quando X=24m  —  t=0,75s  —  X=V_ox.t  —  24=V_ox.0,75  — V_ox=32m/s

c) sem efeito  —  a força resultante sobre a bola é seu peso  —  P=mg  —  a=g  —  com efeito  —  F=3P (para cima) e P (para baixo)  —  F_R=3P – P=2P=2mg  —  a’=2g  —  como a aceleração é proporcional à velocidade, ela também dobrará  —  V’+2.32  —  V’=64m/s

14- a) Y_o=0  —  quando t=0,3s  —  Y=1,2m  —  Y=Y_o + V_oyt + at²/2  —  1,2=0 + 0,3V_oy= + a.(0,3)²/2  —  0,3V_oy + 0,045a=1,2  I

quando t=0,8s  —  Y=1,2m  —  Y=Y_o + V_oyt + at²/2  —  1,2=0 + V_oy.0,8 + a(0,8)²/2  —  0,8V_oy + 0,32a = 1,2  II  —  resolvendo o sistema composto por I e II  —  a=-10m/s²=g  e V_oy=5,5m/s  —  tempo que demora para atingir a altura máxima onde V_y=0  —  V_y=V_oy + at  —  0=5,5 – 10t  —  t=0,55s  —  Y_máx= Y_o + V_oyt + at²/2  —  Y_máx= 0 + 5,5.0,55 – 10(0,55)²/2  —  Y_máx=1,5125m

b) tempo total de movimento t=2.0,55  —  t=1,1s  —  na horizontal  —  X=V_ox.t  —  1,3=V_ox.1,1  —  V_ox=1,18m/s

c) V_o²=V_ox² + V_oy²  —  V_o² = (1,18)² + ((5,5)²  —  V_o²=1,3924 + 37,91  —  V_o=6m/s

15- a) V_o=72km/h/3,6=20m/s  —  V_oy=V_osen20^o=20.0,35  — V_oy=7m/s  —  V_ox=V_ocos20^o=20.0,95  —  V_ox=19m/s  —  tempo que a bola demora para chegar à barreira onde X=9,5m com velocidade constante V_ox=19m/s  —  X=V_ox.t  —  t=9,5/19  —  t=0,5s  —  nesse instante a barreira deverá ter uma altura vertical de  —  Y=V_oyt – gt²/2=7.0,5 – 5.0,25  —  Y=3,5 – 1,25  —  Y=2,25m

b) Tempo que a bola demora para chegar ao gol com velocidade de V_ox=19m/s e distante X=19m do ponto de lançamento  —  X=V_oxt  —  t=19/19  —  t=1s  —  nesse instante a bola terá uma altura vertical de Y=V_oyt – gt²/2=7.1 – 5.1  —  Y=2m (altura da bola ao entrar no gol)  —  altura da trave=2,4m  —  a bola entra no gol 0,4m abaixo da trave.

c) Tempo que a bola demora para atingir a altura máxima onde V_y=0  —  V_y=V_oy – gt  —  0=7 – 10t  —  t=0,7s  —  nesse instante  —  X=V_oxt=19.0,7  —  X=13,3m  —  Y=h_máx=V_0yt – gt²/2=7.0,7 – 5.0,49=4,9 – 2,45  —  h_máx= 2,45m  —  o tempo que ela

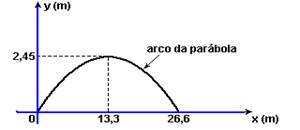
demora para retornar ao solo é o dobro do tempo que demora para atingir h_máx  —  t=2.13,3  —  t=26,6s 

16- a) Colocando o referencial no ponto de lançamento e aplicando Torricelli no ponto de altura máxima onde v_y=0 e h=1,8m  — 

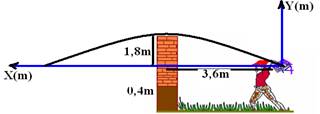
V²=V_oy² – 2gh  —  0²=(V_osenβ)² -2.10.1,8  —  V_osenβ=√36  —  V_osenβ=6  —  tempo que demora para atingir h_máx  —  V_y = V_oy – gt  —  0=V_osenβ – 10t  —  0=6 – 10t  — t=0,6s

b) eixo vertical  —  V_osenβ=6  —  senβ=V_o/6  —  eixo horizontal  —  quando t=0,6s  —  X=3,6m  —  X=V_oxt  —  3,6=V_ocosβ.0,6  —  V_ocosβ=6  —  cosβ=V_o/6  —  tgβ=senβ/cosβ=V_o/6 x 6/V_o  —  tgβ=1  —  β=45^o

17- a) V_ox=V_ocos53^o=100.0,60  —  V_ox=60m/s  —   V_oy=V_osen53^o=100.0,80  —  V_oy=80m/s  —  quando t=12s  —  X=V_oxt=60.12  —  X=720m  —  Y=V_oyt – gt²/2=80.12 – 5.(12)²=960 – 720  —  Y=240m

b) A força resultante é o peso do projétil, de direção vertical e sentido para baixo e de intensidade P=mg=0,1.10  —  P=1,0N

 

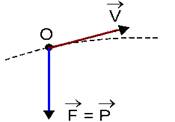
18- a) Observe a figura abaixo, onde você deve decompor V em suas componentes vertical V_y e horizontal V_x

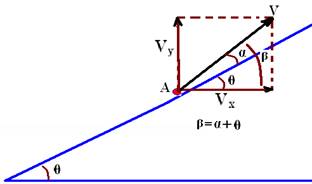
V_x=Vcosβ  —  V_x=Vcos(α + θ)  —  V_y=Vsenβ  —  V_y=Vsen(α + θ)  —  equação horária segundo a horizontal X  —  X=V_oxt=V_xt  —  X=V.cos (α + θ).t  —  Y=V_yt – gt²/2  — Y=Vsen (α + θ).t – gt²/2

b) Isolando t em X=Vcos(α + θ)t  —  t=X/Vcos(α + θ) que, substituída em Y=Vsen(α + θ)t – gt²/2  —  Y=Vsen(α + θ).X/Vcos(α + θ) – g(X/Vcos(α + θ))²/2  —  Y=tg(α + θ) – g.X²/2V²cos²(α + θ)

19- V_oy=V_osen45^o  —  V_oy=√2/2V_o  —  V_ox=V_ocos45^o  —  V_ox=√2/2V_o  —  cálculo do tempo de subida que ocorre na altura máxima quando V_y=0  —  V_y=V_oy – gt  —  0=√2/2V_o – gt  —  t=√2.V_o/2g (tempo de subida)  —  na horizontal  —  X=s=V_ox2t  —  s=√2/2.V_o2(√2V_o/2g)  —  s=V_o²/g  —  na vertical  —  Y=h==V_oyt – gt²/2=√2/2.V_o(√2.V_o/2g) – g.(√2V_o/2g)²/2  —  h=V_o²/2g – V_o²/4g  —  h=V_o²/4g  —  s/h=V_o²/g x 4g/V_o²  —  s/h=4

20- a) V_ox=V_ocos30^o=100.0,9=90m/s  —  V_oy=V_osen30^o=100.0,5=50m/s  —  tempo para atingir h_máx o que ocorre quando V_y=0  — 

V_y=V_oy – gt  —  0=50 – 10t  —  t=5s  —  o alcance ocorre em t=2.5  —  t=10s  —  X=V_oxt=90.10  —  X=900m 

b) h_máx segundo Simplício  — 

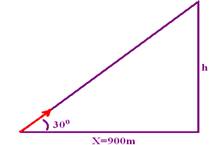
tg30^o=h/900  —  √3/3=h/900  —  1,8/3=h/900  —  h=540m

c) h_máx segundo Salviati  —  V_oyt – gt²/2=50.5 – 5.25/2=250 – 125  —  h_máx=125m   

21- I- V_oy é a mesma (mesmo V₀ e o mesmo ângulo)  —   Na h_máx  —  V_y=0  —  V_y² = V_oy² – 2.g.h_máx  —  0 = V_oy² – 2gh_máx  —  h_máx=V_oy²/2g  —  se g diminui, h_máxaumenta  —  Verdadeira

II – Correta  —  a velocidade do projétil no aponto mais alto da trajetória é nula na Terra e na Lua.

III – V_ox é a mesma  —  X=V_ox.t  —  o alcance horizontal X independe de g, assim X é o mesmo na Terra e na Lua.

IV – Correta  —  a velocidade vertical com que ele é lançado é a mesma, veja I, quem varia é g.

22- Na altura máxima  —  V_y=0 e h=3,2m  —  Torricelli  —  V_y²=V_oy² – 2gh  —  0²=V_oy²– 2.10 3,2  —  V_oy=8m/s  —  R- D

23- I – Verdadeira  —  vê uma composição de dois movimentos, um na vertical e outro na horizontal.

II – Falsa  —  desloca-se em movimento retilíneo uniforme com velocidade horizontal constante.

III – Correta – na vertical o movimento é uniformemente variado com aceleração a=-g.

R- D

24- a) Na h_máx  —  V_y=0  —  h_máx=1,25m  —  Torricelli  —  V_y²=V_oy² – 2gh_máx  —  0²= V_oy² -20.1,25  —  V_oy=5m/s  —  V_y=V_oy – gt  —  0=5 – 10t  —  t₁=0,5s

b) X=V_oxt=V_ox2t₁  —  6=V_ox.1  —  V_ox=6,0m/s

c) Trata-se do tempo que ele demora para percorrer na horizontal, com velocidade de V_ox=6ms a distância X=(7,04 – 3,0)=4,04m  —  X=V_oxt₂=  —  4,04=6t₂  —  t₂=0,67s

25- Bola 1  —  lançamento vertical  —  tempo para atingir h_máx onde V=0  —  V=V_o – gt  —  0=30 – 10t  —  t=3s  —  h_máx= 30.3 – 5.9  —  h_max= 45m

Bola 2  —  lançamento oblíquo  —  quando t=3s  —  h’=V_oyt – gt²/2  —  h’=V_osen30^o.t – gt²/2=50.1/2.3 – 10.9/2=75 – 45  —    —  h’=30m  —  X=V_ocos30^o.t=50.√3/2.3  —  X=127,5m  —  a distância pedida é d, conforme figura abaixo

 

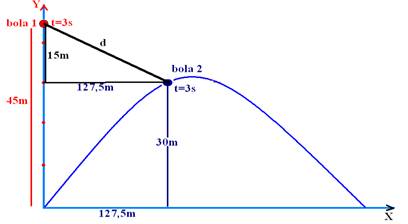
d²=(15)² + (127,5)²  —  d=√225 + 16.256,25  —  d=√16.481,25 m  —  R- D

26- a) V_y=V_osen30^o – gt  —  0=5.0,5 – 10t  —  t=0,25s

b) Cálculo da altura máxima  —  Y=h_máx=Y_o + V_ocos30^o – gt²/2=2 + 0,625 – 0,3125  — h_máx=2,3125m que é menor que a altura da cesta

c) na horizontal  —  X=V_ocos30^ot  —  4=V_o.0,86t —  t=4,6/V_o  —  na vertical  —  Y=Y_o+ V_osen30^ot – gt²/2  —  3=2 + 0,5V_o.(4,6/V_o) – 5(4,6/V_o)²  —  1,3=106/V_o²  — V_o=9,02m/s

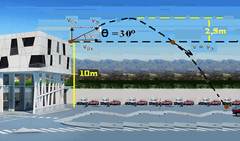
27- Dados: v_o = 10 m/s; h_o = 10 m; q = 30°  —  as componentes horizontal (v_ox) e vertical (v_oy) da velocidade inicial são  — 

V_ox = v_o cos 30° = 10 (0,87) = 8,7 m/s  —  v_oy = vo sem 30° = 10 (0,5) = 5 m/s. 

Verificando cada uma das opções:

a) Altura máxima atingida em relação ao ponto de lançamento  —  V_y²=V_oy² – 2gh  —  0²= V_oy² – 2gh  —  h=V_oz²g=5²/10  — 

h=2,5m  —  em relação ao solo  —  H=2,5 + 10  —  H=12,5m

b) Tempo de subida  —  V_y=V_oy – gt  —  0=5 – 10t  —  t=0,5s

c) Com referencial no solo e orientando a trajetória para cima, o tempo para chegar ao solo é calculado pela função horária do espaço  —  h=h_o + V_oyt – gt²/2  —  h=10 + 5t – 5t²  —  quando chega ao solo h=0  —  0=10 + 5t – 5t²   —  t² – t – 5=0  —  resolvendo a equação  —  t @ 2,8 s.

d) Correta. Ao passar novamente pela mesma altura a pedra possui a mesma energia potencial inicial  —   considerando o sistema

 conservativo, então a pedra tem também a mesma energia cinética, portanto a mesma velocidade, em módulo, ou seja, se ela é lançada com velocidade de 10m/s, ao retornar passará por esse mesmo ponto com velocidade de -10m/s.

R- D

28- Dados  —  v_o = 10 m/s; q = 45°; g = 10 m/s².

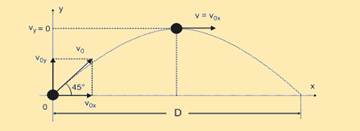
V_ox = v_o cos 45° = 10.√2/2  —  V_ox=5√2m/s  —  v_oy = v_o ­sen 45° = ­5√2m/s  —  no eixo y o movimento é uniformemente variado, com a = –g  —  tempo de subida (t_sub), notando que no ponto mais alto v_y = 0  —  v_y = v_oy – g t  —  0 = 5√2 – 10 t_sub­  — 

T_sub =√2/2 s  —   tempo  de subida é igual ao de descida  —  tempo total (t_t)  —  t_t=2t_sub  —  t_t=√2s  —  no eixo x o movimento é uniforme, com velocidade igual a v_ox  —   alcance horizontal (D)  —   D = v_ox t_t = 5.√2.√2  —  D=10m  —  R- E

29- Dados: g = 10 m/s²; √2= 1,4; q = 45°; v_o = 20 m/s.

a) Considere desprezível a resistência do ar e que, ao matar a bola, o pé do artilheiro esteja bem próximo ao chão  —  então você pode considerar o ponto de lançamento e o ponto de chegada pertencente a um mesmo plano horizontal  —  no ponto mais alto a componente vertical da velocidade (v_y) é nula  —  v_y = v_oy – g t  Þ  0 = v_osen q – g t_s  —  0=20.sen45^o – 10t_s  —  t_s=20.√2/2/10  —

t_s=√2 s  —  tempo total =t_subida + t_descida  —  t_total= √2 + √2   —  t_total=2√2 s  —  na horizontal o movimento é uniforme  — velocidade V_x (constante) —  v_x  = v_o cos q = v_o cos 45° = 20.√2/2 m/s  —  V_x=10√2 m/s  —  alcance horizontal  —  x=V_x.t=(10√2).(2.√2)  —  x=40m

b) A velocidade média (v_m) do artilheiro pode ser calculada considerando que ele percorreu a distância (DS) de 16 m enquanto a bola esteve no ar  —  V_m=ΔS/Δt=16/2√2  —  V_m=4√2=4.1,4  —  V_m=5,6m/s=20,16km/h

30- Analisando apenas a incorreta, que é a 02  —  a componente horizontal está correta, pois no eixo x o movimento é uniforme, porém, no eixo y, o movimento é uniformemente variado e a equação correta é  —  y = y_o + v_oy t –  gt²/2  —  y_o=0  —  V_oy=

V_o senθ  —  Y=(V_osenθ)t – gt²/2 

R- (01 + 04 + 08 + 16)=29    

31- Para um observador no interior do trem que se desloca em movimento retilíneo e uniforme, o alcance de um objeto lançado horizontalmente só depende da intensidade da velocidade  do objeto  —  assim, caso a bola fosse arremessada em sentido oposto ao do deslocamento do trem, a distância entre o ponto de arremesso e o ponto de impacto também seria igual a 5 m  —  não haveria diferença, pois a queda só é influenciada por g  —  logo, seria 5m ao contrário da origem  —  R- B

32- O tempo de queda é calculado exclusivamente pelo movimento vertical (queda livre da altura de 1m com a=g=10m/s²  —  h=gt²/2  —  1=10t²/2  —  t=√0,2  —  t=0,447s  —  R- C

33- O tempo de subida é igual ao tempo de descida o que ocorre quando V_y=0  —  V_y=V_oy – gt  —  0=V_osenθ – gt  —  t=V_osenθ/g  —  tempo no ar  —  t_total=2t=2V_osenθ/g  —  sendo 2V_o e g constantes, o tempo de permanência no ar depende apenas do ângulo θ com a horizontal  —  quanto menor θ, menor será senθ e, consequentemente menor t_total  —  R- B

 

34-

 Decompondo a velocidade inicial  —  vertical  —  V_oy=V_o.senα  —  horizontal  —  V_ox=V_o.cosα  —  na vertical trata-se de um lançamento vertical para cima com velocidade inicial V_oy=V_o.senα, aceleração da gravidade (-g) e, na altura máxima h=0,30x a velocidade vertical V_y=0  —  equação de Torricelli  —  v_y² = (V_o.senα)² + 2.(-g).h  —  0² = (V_o.senα)² – 2.g.0,30x  —  x=V_o².sen²α/6 (I)  —  tempo de subida  —  V_y=V_oy– gt  —  0=v_o.senα – 10t  —  t=V_o.senα/10  —  t_total=(tempo de subida + tempo de descida)=2t  —  t_total=2.V_o.senα/10  —  t_total= V_o.senα/5  —  segundo a horizontal trata-se de movimento retilíneo uniforme com velocidade constante V_x=V_ox=V_o.cosα  —  V_x=x/t_total  —  V_ocosα=x/V_o.senα/5  —  x=v₀.cosα.V_o.senα/5  —  x=v₀².cosα.senα/5 substituindo (I) em x  —  V_o².sen²α/6 = v₀².cosα.senα/5  —  senα/6= cosα/5  —  senα/cosα=6/5  —  tgα=1,2  —   pela tabela α=50^o  —  R- D

 

35-

 02- Colocando os dados fornecidos no sistema de eixos cartesianos  —  equação  —  y(x) = a(x – x1).(x – x2)  — 

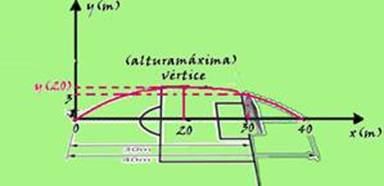
colocando a origem do sistema no ponto de lançamento da bola  —  x1=0 e x2=40)  —  y(30) = a(x – 0).(x – 40) quando x=30m,  y=3m  —  3 = a.(30 – 0).(30 – 40)  —  3=a.30.(-10)  —  a= – (1/100)  —  a altura máxima ocorre na metade da abscissa x, ou seja, quando x=20 m  —  y(20)=a.(x – x1).(x – x2)  —  y(20)=- (1/100). (20 – 0).(20 – 40)  —  y(20)= – (1/100).(20).(-20)  —  y(20)=4 m  —  R- B

 

36- Sendo a perda de energia durante a colisão desconsiderada neste lançamento obliquo você pode considerar  todo o movimento horizontal (segundo x) como sendo uniforme de velocidade constante Vox=Vosenθ=10.0,6  —  Vox=6m/s  —  com essa velocidade constante, excluindo o tempo do choque a bola percorre ∆x=6,6m  —  Vox= ∆x/∆t  —  6=6,6/∆t  —   ∆t=1,1s  —  o intervalo de tempo total de movimento da bola inclui o tempo do choque (1/10)s  —   ∆ttotal=1,1 + 0,1=1,2s  —   ∆ttotal=1,2s  —  cálculo da velocidade vertical (Vy) da bola ao chegar ao solo, lançada verticalmente para baixo com Voy=Vo.cosθ=10.0,8  —  Voy=8m/s  —

Trata-se de um lançamento vertical para baixo com velocidade inicial Voy=8m/s, percorrendo h=1,8m num local onde g=10m/s2  —  equação de Torricelli  —  Vy2 = Voy2 + 2.g.h  —  Vy2=82 + 2.10.1,8  —  Vy=10m/s  —  durante a colisão vertical, o impulso da força F é igual à variação da quantidade de movimento  —   I=∆Q  —  I=F.∆t=F.0,1  —  ∆Q=mV – mVo=0,6.9 – 0,6.(-10)  —

∆Q=11,4kg.m/s  —  I=∆Q  —  0,1F=11,4  —  F=114N

 

37-

Trata-se de um lançamento oblíquo, representado na figura, onde foram colocados os respectivos dados fornecidos no enunciado  –

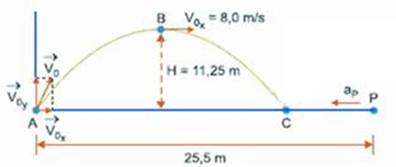
—  cálculo de Voy  —  na altura máxima (H=11,25m) a velocidade vertical Vy é nula (Vy=0)  —  equação de Torricelli  — 

Vy2 = Voy2 + 2.(-g).H  —  02 = Voy2 – 2.10.11,25  —  Voy=√(225)  —  Voy=15m/s  —  tempo de subida  —  Vy = Voy – gt  —  0=15 – 10t  —  t=1,5s  —  para que Protásio consiga alcançar a bola no mesmo nível do lançamento, ele deve alcança-la no ponto C, onde, desde que partiu, ela demora t=1,5 (metade do percurso horizontal) + 1,5s (outra metade do percurso horizontal)  —  t=3s  —  cálculo do alcance horizontal x lembrando que,  —  Vox é constante e durante todo o movimento horizontal tem intensidade  Vox=8m/s  —  x=Vox.t=8.3=24m  —  aceleração de Protásio  —  até alcançar a bola ele percorreu ∆S no mesmo tempo que a bola permaceu no ar, ou seja, t=3s  —  ∆S=22,5 – 24

=1,5m  —∆S= Vot + at2/2  —  como ele partiu do repouso, Vo=0  —  1,5=0 + a.32/2  —  a=1,5/4,5  —  a=1/3m/s2  —  R- B

 

Voltar para os exercícios sobre lançamento oblíquo