Resolução comentada dos exercícios LANÇAMENTO HORIZONTAL

Resolução comentada dos exercícios sobre  LANÇAMENTO HORIZONTAL

 

01- R- E – veja teoria

02- R- C – em todo lançamento horizontal, a componente V_0x=V_o=V_x=constante.

03- O tempo que o destróier dispõe é o tempo que a bomba demora para cair e percorrer a distância vertical de 8km  —  Y=8.000m  —  Y=gt²/2  —  8.000=10t²/2  —  t=√1.600  —  t=40s

04- Tempo que a pedra demora para atingir a superfície da água, ou seja, percorrer verticalmente Y=1m  —  Y=gt²/2  — 

1=5t²  —  t=√0,2s  —  em t=√0,2=0,45s ela percorre na horizontal X=3m  —  X=V_o.t  —  3=V_o.0,45  —  V_o=6,7m/s

05- Y=gt²/2  —  0,8=5t²  —  t=0,4s  —  X=V_ot  —  0,8=V_o.0,4  —  V_o=2,0m/s  —  R- D

06- tempo de queda  —  Y=gt2/2  —  5=5t2  —  t=1s (é sempre o mesmo, depende apenas da altura vertical)  —  velocidade mínima (limite inferior de R)  —  X=V.t  —  1=V.1  —  V=1ms  —  limite posterior (velocidade máxima)  —  X=V’.t  —  4=V’.1  —  V’=4ms  —  R- D

07- O tempo t de queda aumenta, pois a altura aumenta  — como X1=1m e X2=4m permanecem constantes, V1 e V2 devem diminuir para manter a igualdade X=V.t  —  R- E

08- Velocidade vertical com que ela chega ao solo  —  V_y²=2.g.h=2.10.0,6  —  V_y²=12  —  velocidade horizontal com que ela chega ao solo  —  é a mesma de lançamento  —  V_x=2m/s  —  velocidade resultante V com que ela chega ao solo

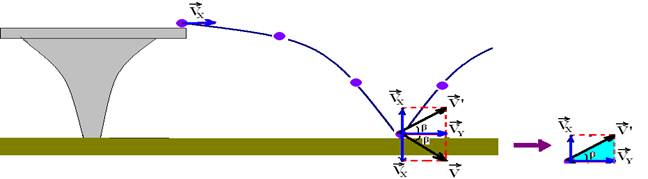
A intensidade da velocidade resultante com que ela chega ao solo vale V²=V_y² + V_X²=12 + 4  —  V=√16  —  V=4m/s  —  mas, como o choque é perfeitamente elástico, ela retorna com velocidade resultante de mesma intensidade, ou seja, V’=V=4m/s  —  no triângulo hachurado da figura acima  —  senβ=V_y/V’=√12/4=2√3/4=√3/2  —  β=60^o  —  R- C

09- A ordem de chegada ao solo, independente das massas , depende da altura de queda  —  menor altura, menos tempo de queda  —  R- C

10- a) Lançamento horizontal do sistema (bloco + projétil) que independe da massa  —  tempo que demora para chegar ao solo na vertical percorrendo a altura Y=1,25m  —  Y=gt²/2  —  1,25=5t²  —  t=0,5s  —  nesse tempo ele percorre na horizontal X=5m com velocidade V_o  —  X=V_ot  —  5=V_o.0,5  —  V_o=10m/s

b) choque inelástico  —  movem-se juntos após o mesmo  —  princípio da conservação da

quantidade de movimento  — quantidade de movimento  –Q_antes=m_pV_p + m_bV_b=0,02.V_p + 0,480.0  —  Q_antes=0,02.V_p  —  Q_depois=(m_p + m_b).V=(0,02 + 0,480).10  —  Q_depois=5kg.m/s  —  Q_antes=Q_depois  —  0.02V_p=5  — V_p=250m/s

11- Não, pois enquanto o alvo permanece imóvel, o projétil, durante todo seu movimento estará caindo, sujeito à aceleração da gravidade e chegará ao alvo numa posição abaixo daquela em que ele mirou.

12- Como o alvo permanece imóvel, o projétil, durante todo seu movimento estará caindo, sujeito à aceleração da gravidade e chegará ao alvo numa posição abaixo daquela em que ele mirou  —  tempo que o projétil demora para percorrer a distância horizontal de X=30m com V_o=600m/s (constante)  —  X=V_ot  —  30=600t  —  t=0,05s  —  nesse tempo ele desce uma altura Y de  —  Y=gt²2=5.(0,05)²  —  Y=5.(0,0025)=0,0125m=1,25cm  —  R- E

13- Distância vertical (altura do prédio) percorrida em 2s  —  Y=gt²/2=5.4=20m  —  número de andares  —  n=altura do prédio/altura de cada andar=20/2,5  —  n=8 andares  —  R- D

14- tg45^o=D/H  —  1=D/H  —  D=H  — na vertical  —   H=gt²/2  —  H=5t²  —  na horizontal  —  X=Vt  —  D=H=10t  —

10t=5t²  —  t=2s  —  D=H=10.2=20m  —  R- A

15- V_o=144km/h=144/3,6  —  V_o=40m/s  — tempo que o saco demora para chegar ao solo na direção vertical  —  Y=gt²/2  —  500=5t²  —  t=10s  —  nesse instante o alvo deve estar a uma distância horizontal de X=V_ot=40.10  —  X=400m  —–  R- D

16- tempo que demora para percorrer Y=0,80m na vertical  —  Y=gt²/2  —  0,80=5t²  —  t=0,4s  —  nesse tempo ele percorre na horizontal X=2,8m com velocidade V_o  —  X=V_ot  —  2,8=V_o.0,4  —  V_o=7,0m/s  —  R- D

17- R- E  —  (veja teoria)

18- V_o=360/3,6=100m/s  —  t=0  —  X_o=0  —  t=1s  —  X₁=V_ot=100.1=100m  —  t=2s  —  X=V_ot=100.2=200m  —  a distância entre os pontos de impacto será de 100 m.

19- Por inércia as três caixas continuaram em movimento com a mesma velocidade horizontal do avião de 360 km/h  —  desta forma os impactos no solo ocorrerão sobre a mesma linha reta, separadas pela distância percorrida pelo avião durante aquele 1 s entre os lançamentos das caixas  —   velocidade de 360 km/h corresponde a 100 m/s e desta forma a distância entre os pontos de impacto será de 100 m.

20- (01) Correta  —  a trajetória somente é parabólica quando a resistência do ar é nula.

(02) Errada  —  a componente horizontal da velocidade só se mantém constante se a resistência do ar é nula.

(04) Errada  —  a força de arrasto tem sentido oposto ao da velocidade em cada ponto, sempre tangente à trajetória.

(08) Errada  —  mesma justificativa de (01) e (02).

(16) Correta  —   componente horizontal da força de resistência do ar faz diminuir a componente horizontal da velocidade, que tende para zero, enquanto a componente vertical da resistência do ar tende a equilibrar o peso. Assim o movimento tende a se tornar retilíneo e uniforme, na direção vertical. 

R- (01+ 16) = 17

21- Com a mola comprimida de X a energia potencial elástica armazenada na mesma vale  —  E_p=kX²/2  —ao deixar o contato com a mola toda a energia potencial elástica é transformada em energia cinética de valor E_c=mV²/2  —  considerando o sistema conservativo (sem atrito) essas energias se igualam  —  KX²/2 = mV²/2  —  V²=KX²/m  —  utilizando agora a conservação da energia mecânica  —  no topo do plano  —  E_MA=mV²/2 + mgh  — no solo chega com velocidade V’  —  E_MB = mV’²/2 + mg.0  —  E_MA = E_MB  —  mV²/2 + mgh=mV^’2/2  —   V’=√(2gh + KX²/m)  —  R- A

22-Quando a menina abandona a bola, a menina continua em movimento retilíneo e a bola executa um lançamento horizontal  —  as velocidades horizontais da bola e da menina são as mesmas e valem V_m=V_s=10,8/3,6=3m/s  —  então, a distância horizontal percorrida pela menina e pela bola é a mesma  —  S_b=S_m=V.Δt=3.0,5  —  S_b=S_m=1,5m  —  R- E

 

Utilize as informações a seguir para responder às questões de números 23 e 24

Três bolas − X, Y e Z − são lançadas da borda de uma mesa, com velocidades iniciais paralelas ao solo e mesma direção e sentido.

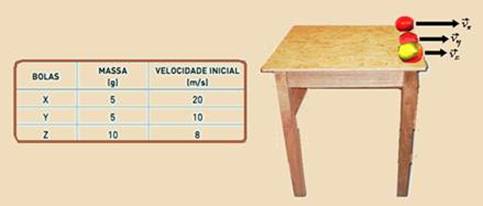
A tabela acima mostra as magnitudes das massas e das velocidades iniciais das bolas.

 

23-

Trata-se de um lançamento horizontal que segundo o eixo y é uma queda livre com V_oy=0 e sob aceleração da gravidade g  —  h=V_oyt + gt²/2=0 + gt²/2  —  h=gt²/2  —  observe que, como h e g são os mesmos, o tempo de queda também será o mesmo  —  R- D

 

24-

Em todo lançamento horizontal a velocidade horizontal é constante, igual à velocidade de lançamento, independente da massa do corpo  —  assim, a esfera que é lançada com maior velocidade consegue o maior alcance  —  R- C

25-

Como o exercício pede a altura você deve utilizar apenas o movimento parcial na direção vertical (eixo Y)

A projeção da aceleração da gravidade () é o próprio .  Assim, na direção vertical tem-se um movimento uniformemente variado (MUV), ou seja, um lançamento vertical para cima, com aceleração igual à aceleração da gravidade  e velocidade inicial de lançamento  Voy, tal que Voy=Vo.senα, onde α é o ângulo de lançamento..   

 

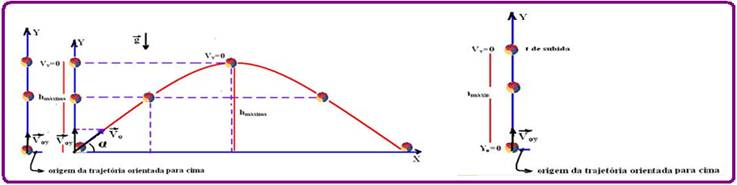
V_oy=V_o.senα – componente vertical de V_o  —  Y – altura num instante qualquer t  —  Y_o  —  altura inicial  —  g – aceleração da gravidade  —  orientando o eixo Y para cima tem-se um lançamento vertical de equações  —  S=Y  —  S_o=Y_o=0  —  V_o=V_oy=V_o.senα  —  a=-g  —  equação da posição (dos espaços) ou da altura Y  —  S=S_o + V_o.t + a.t²/2  —  Y=Y_o + V_oy.t – gt²/2  —  Y=0 + V_oy.t – gt²/2  —  Y= V_oy.t – gt²/2, com V_oy=Vo.senα. 

V_oy=V_o.senθ=30.0,5  —  V_oy=15m/s  —  Y=15.1 – 10.1²/2  —  Y=10m  —  R- A

 

 Voltar para os Exercícios