Resoluções dos exercícios gráficos do MUV

Resoluções dos exercícios sobre gráficos do MUV

01-

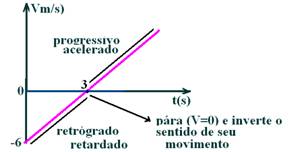
a) S_o=8m (ponto em que a parábola encosta na ordenada “eixo S”, ou seja, ponto quando t=0). Inverte o sentido de seu movimento no instante t_i=3s (vértice da parábola, onde V=0, onde o movimento passa de retrógrado para progressivo). Passa pela origem dos espaços quando S=0, ou seja, nos instantes t=2s e t=4s.

b) O movimento é progressivo quando o móvel se desloca no sentido dos marcos crescentes (V>0) o que ocorre após t=3s e retrógrado quando o móvel se desloca no sentido dos marcos decrescentes (V<0) o que ocorre entre 0 e 3s.

c) O movimento é acelerado após 3s, pois a e V tem mesmo sinal (a é positiva “a concavidade da parábola é para cima” e V é positiva “se desloca no sentido dos marcos crescentes”).

O movimento é retardado entre 0 e 3s 3s, pois a e V tem sinais contrários (a é positiva “a concavidade da parábola é para cima” e V é negativa “se desloca no sentido dos marcos decrescentes”).

d) S_o=8m — quando t=2s — S=0 — S=S_o + V_o.t + a.t²/2 — 0=8 + V_o.2 + a.2²/2 — 2.a + 2.V_o = -8 I — quando t=4s — S=0 — S=S_o + V_o.t + a.t²/2 — 0=8 + V_o.4 + a.4²/2 — 8.a + 4.V_o = -8 II — Resolvendo o sistema composto por I e II — a=2m/s² e V_o=-6m/s — S=S_o + V_o.t + a.t²/2 — S= 8 – 6.t + t²

e) V=V_o + a.t — V= -6 + 2.t — gráfico VXt — V=0 — 0= -6 + 2.t — t=3s — V_o=-6m/s — como é uma função do primeiro grau seu gráfico é uma reta que pode ser definida por apenas dois pontos.

f) A aceleração é constante e vale a=2m/s²e seu gráfico é uma reta paralela ao eixo dos tempos

02- Trecho I – MUV (ramo de parábola) com aceleração positiva “a>0” (concavidade para cima) e velocidade positiva “V>0” (se desloca no sentido dos marcos crescentes,movimento progressivo) — o movimento é acelerado, pois a e V tem mesmo sinal.

Trecho II – MUV (ramo de parábola) com aceleração negativa “a<0” (concavidade para baixo) e velocidade positiva “V>0” (se desloca no sentido dos marcos crescentes,movimento progressivo) — o movimento é retardado, pois a e V sinais contrários.

Trecho III – MU (reta oblíqua) com V constante e negativa (se desloca no sentido dos marcos decrescentes, movimento retrógrado).

Trecho IV – MUV (ramo de parábola) com aceleração positiva “a>0” (concavidade para cima) e velocidade negativa “V<0” (se desloca no sentido dos marcos decrescentes, movimento retrógrado) — o movimento é retardado, pois a e V sinais contrários.

Trecho V – MUV (ramo de parábola) com aceleração positiva “a>0” (concavidade para cima) e velocidade positiva “V>0” (se desloca no sentido dos marcos crescentes, movimento progressivo) — o movimento é acelerado, pois a e V sinais contrários.

03- A aceleração é máxima onde a curva tem maior inclinação em relação à horizontal — R- A

04- V_o=4m/s — a=(V – V_o)/(t – t_o)=(12 – 4)/(4 – 0) — a=2m/s² — V= V_o + a.t — V=4 + 2.7 — V=18m/s (velocidade no instante t=7s) — a distância percorrida corresponde à área hachurada do gráfico abaixo

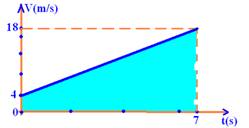
ΔS=(B + b).h/2=(18 + 4).7/2 — ΔS=77m

05- ΔS=S – S_o=9 – 0=9m — V_o=0 — V=6m/s — Torricelli — V² = V_o² + 2.a.ΔS — 36=0 + 2.a.9 — a=2m/s² — R- B

06- a) Na vertical — S_o=0 — t=0,3s — S=1,2m — S=S_o + V_o.t + a.t²/2 — 1,2=0 + V_o.0,3 + a,(0,3)²/2 — 0,3.V_o + 0,045.a=1,2 — V_o + 0,15.a=4 I — t=1,1s — S=0 — S=S_o + V_o.t + a.t²/2 — 0=0 + V_o.1,1 + a.(1,1)²/2 — 1,1V_o + a.0,605=0 II — resolvendo o sistema composto por I e II — a=-10m/s² — V_o=5,5m/s — a altura máxima ocorre quando V=0 (ela pára para começar a descer) que vale 0,55s pelo gráfico — S=S_o + V_o.t + a.t²/2 === S_máx=0 + 5,5.(0,55) – 10.(0,55)²/2 — S_máx=3,025 – 1,5125 — S_máx=1,5125m

b) Na horizontal a velocidade é constante e vale V_m=ΔS/Δt=1,3/1,1 — V_m=1,18m/s

c) V_o=5,5m/s (veja item a)

07- V_B=0 (vértice da parábola “pára para começar a inverter o sentido de seu movimento”) — quanto mais inclinada a curva em relação à horizontal, maior será a velocidade, ou seja, V_A>V_C — R- B

08- a) Ficou parado entre 1h e 1,8h, ou seja, 48minutos, no km100 (veja gráfico)

b) V_m=ΔS/Δt=(120 – 0)/(3 – 0) — V_m=40km/h (lembre-se de que o tempo de parada está sempre incluído)

09- Os gráficos não podem se referir ao mesmo movimento; se a aceleração é uma constante negativa, a velocidade é uma reta com inclinação negativa, ou seja, está diminuindo. Logo, a função posição x(t) só pode ser representada por uma parábola com concavidade para baixo, ao contrário do que está mostrado.

10- a)Os deslocamentos de cada carro são fornecidos pelas áreas hachuradas nos gráficos abaixo:

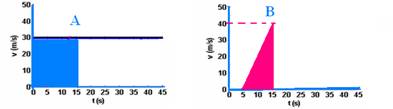
ΔS_A=b.h=15.30=450m — ΔS_B=b.h/2=10.40/2=200m — d=450 – 200 — d=250m

b) Se encontram no instante t em que efetuaram o mesmo deslocamento, ou seja, a área em cada gráfico deve ser a mesma:

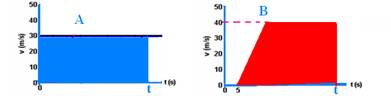
ΔS_A=b.h=t.30=30.t — ΔS_B=(B + b).h/2=(t – 5 + t – 15).40/2=40t – 400 — no encontro, percorreram a mesma distância — ΔS_A=ΔS_B — 30t=40t – 400 — t=40s

11- a) ΔS=soma das áreas=3.8/2 + (4 + 2).12/2 + 2.12/2 — ΔS=60m

b) V_m= ΔS/ Δt=60/15 — V_m=4m/s

12- Entre 0 e t₁ — velocidade aumentando, aceleração positiva e concavidade da parábola para cima — entre t₁ e t₂ — velocidade constante, aceleração nula, movimento uniforme com reta ascendente e movimento progressivo — entre t₂ e t₃ — velocidade diminuindo, aceleração negativa e parábola com concavidade para baixo — R- D

13- Trata-se de uma queda livre com a=-g (aceleração da gravidade) com concavidade para baixo e a velocidade a partir de zero e aumentando em módulo (movimento retrógrado acelerado) — R- B

14- Entre 0 e 4s — a=4m/s² — V=V_o + at — V=0 =4.4 — V=16m/s — entre 4s (onde V_o=16m/s) e 8s — V=V_o + at — V=16 -2.4 — V=8ms

15- Durante 1s ele se move com velocidade constante de 20m/s e depois, sua velocidade diminui até zero segundo uma reta, pois se trata de um MUV com desaceleração constante — R- D

16- Parte do repouso — V_o=0 — entre 0 e 2s a aceleração é positiva e vale 0,5m/s² — V=V_o + at=0 + 0,5.2=1m/s e sua velocidade variade 0 a 1m/s — ntre 2s e 4s, a aceleração é nula e ele segue em movimento uniforme com velocidade constante de 1m/s —

R- E

17- entre 0 e 10s — V_o=0 — V=V_o + at=0 + 1.10=10m/s — entre 10s e 20s — V_o=10m/s — V=V_o + at=10 + 2.10=30m/s — entre 20s e 50s — a aceleração é nula e a velocidade constante de 30m/s — entre 50s e t ele freia e pára com sua velocidade variando de 30m/s para 0 — V=V_o + at — 0=30 -1.t — t=30s — t_f=50 + 30=80s

Construindo o gráfico Vxt

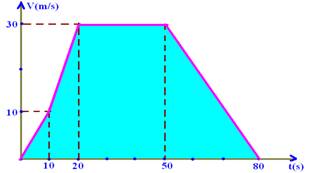
ΔS_total=soma das áreas=10.10/2 + (30 + 10).10/2 + 30.30 + 30.30/2 — ΔS_total=1.600m — R- A

18- Colocando a origem da trajetória vertical no ponto de lançamento e orientando-a para baixo, na subida o movimento é retrógrado retardado e na descida progressivo acelerado (observe atentamente figuras abaixo)

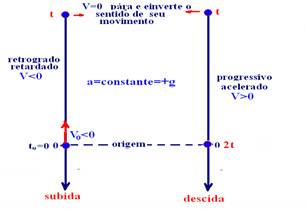
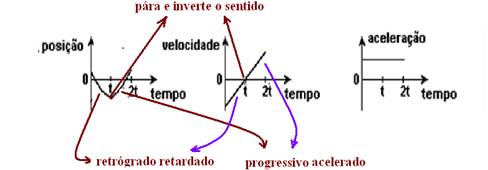
R- D

19- Veja explicação baseada nos gráficos abaixo:

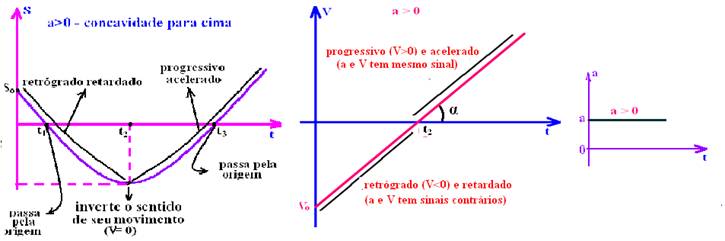
R- D

20- R- B — a aceleração do móvel A é positiva e diferente de zero e o móvel B está em movimento uniforme com velocidade constante e aceleração nula.

21- O vértice da parábola é o ponto onde ocorre a inversão do sentido do movimento. Observe que no gráfico existem três vértices —

R- D

22- 1 – V₁>0 — movimento progressivo (se move no sentido dos marcos crescentes) e a₁<0 (parábola com concavidade para baixo)

2 – V₂<0 — movimento retrógrado (se move no sentido dos marcos decrescentes) e a₁<0 (parábola com concavidade para baixo)

R- D

23- Veja pela resolução anterior que, nesse intervalo de tempo, V₁ é sempre positiva e V₂sempre negativa e, assim, elas não se igualam — R- E

24- S_oII=0 e supondo V_oII=0 a equação do móvel II, que é um MUV é S=S_o + V_o.t + at²/2 — t=15s — S=225m — 225=0 + 0 + a.15²/2 — a=2m/s² — V=V_o + at=0 +2.15 — V=30m/s — R- D

25- Entre 0 e 2s — a=(V – V_o)/(t – t_o)=(14 – 26)/(2 – 0) — a=-6m/s² — após 2s, V é constante e assim, a=0 — R- A

26- V=V_o + at — 20=0 + a.10 — a=2,0m/s² — ΔS=area=b.h/2=5.10/2=25m — R- C

27-

a) O gráfico solicitado entre t = 0 e t = 10 s.

b) Se x = 5 + 16.t – 2.t² — v = 16 – 4.t — v = 16 – 4.4 = 16 – 16 = 0 m/s

c) t=o — S_o=5m — t=5s — S=5 + 16.5 -2.25 — S=35m — deslocamento — ΔS=S – S_o=35 – 5=30m — distância percorrida d — até parar ele demora — V=Vo +a.t — 0=16 – 4t — t=4s e percorre se desloca até o marco — S=5 +16.4 -2.16=37m — entre 4s e 5s ele retorna ao marco S=35m

d ida=(37 – 5)=32m + 2 (volta) — d=34m

28- a) Parte do repouso — V_o=0 — entre 0 e 20s — V=V_o + at — V=0 + 2.20 — V=40m/s — entre 20s e 50s — V=V_o + at=40 – 1.30 — V=10m/s — veja gráfico abaixo

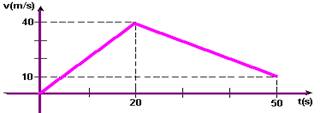
b) A distância percorrida é fornecida pela área hachurada da figura abaixo

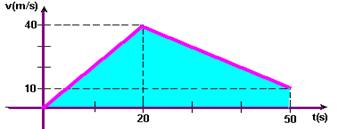
d=b.h/2 + (B + b).h/2=20.40/2 + (40 + 10).30/2 — d=1.150m

29- Sendo o movimento acelerado o gráfico posição x tempo é um arco de parábola com concavidade para cima e a velocidade aumenta de modo uniforme, assim o gráfico velocidade x tempo é uma reta com inclinação ascendente — R- D

30- Entre 0 e 6s — V_I=V_o + a_It_I=2 + 4.6 — V_i=26 cm/s — entre 6s e 10s — V_I=V_o=26cm/s — V_II=V_o + a_IIt_II=26 + (-3).4 —

V_II=14 cm/s — V_II=V_o=14 cm/s — V_III=V_o + a_III.t_III=14 + 4.6 — V_III=38 cm/s

31- 01) Correta — no gráfico representado a seguir, seja k o coeficiente angular (declividade) da reta secante à curva entre os

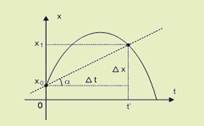
instantes 0 e t’ — k=tgα=(X₁ – X_o)/(t’ – 0)=V_m=ΔX/Δt.
02) Falsa — no diagrama D, no intervalo considerado, a declividade da reta tangente à curva dada está aumentando (em módulo) logo o módulo da velocidade está aumentando — portanto, o movimento é acelerado.

04) Falsa — no instante considerado, o móvel está numa posição negativa (antes da origem).

08) Falsa — no intervalo considerado, o corpo está se deslocando para posições cada vez mais negativas, portanto afastando-se da origem (em movimento retrógrado retardado).

16) Correta — nesse instante, a reta tangente à curva é horizontal, tendo declividade (coeficiente anular) nula.

32) Falsa — nesse intervalo, em módulo, o coeficiente angular da reta tangente está diminuindo, logo o movimento é uniformemente retardado.

64) Correta — pode corresponder a um lançamento vertical para cima com trajetória orientada para baixo (v_o < 0), sendo o ponto de lançamento acima do plano de referência (x_o < 0), como indicado no esquema a seguir.

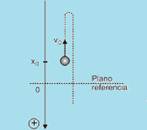
R- (01 + 16 + 64) = 81

32- Trata-se de um gráfico de aceleração ´ tempo — analisando-o você pode afirmar que a aceleração é constante e não nula nos intervalos C e G e nula no intervalo E, onde a velocidade é constante — R- A

33- Sendo a trajetória é retilínea, a aceleração restringe-se à componente tangencial (), que, em módulo, é igual a aceleração escalar (a), dada pela taxa de variação da velocidade (Dv) em relação ao tempo (Dt) — a=ΔV/Δt:

I. a_I = Þ a_I = 10 m/s².

II. a_II = 0 (não houve variaçمo da velocidade)

III. a_III = Þ a_III = –5 m/s².

R- C

34- Nos intervalos de tempo em que a velocidade escalar é constante (1 s a 2 s; 3 s a 4 s e 5 s a 6 s) a aceleração escalar é nula — nos intervalos 0 a 1 s; 2 s a 3 s; 4 s a 5 s e 6 s a 7 s, a velocidade varia linearmente com o tempo, sendo, então, a aceleração escalar é constante.

De 0 a 1 s: a = — de 2 s a 3 s: a = m/s²; — de 4 s a 5 s: a = m/s²; — De 6 s a 7 s:

a = m/s².

R- A

35- Analisando cada intervalo:

– De 0 a 3 s: o movimento é uniformemente acelerado; a aceleração escalar é — a₁ = ΔV₁/Δt₁=8/3=2,7m/s² — o espaço percorrido é calculado pela “área” de 0 a 3 s — ΔS₁=3.8/2 — ΔS₁=12m.

– De 3 s a 5 s: o movimento é uniforme, com velocidade escalar v₂ = 8 m/s — o espaço percorrido é — DS₂ = v₂Dt₂=8´2

DS₂=16 m.

– De 5 s s 7 s: o movimento é uniformemente retardado; a aceleração escalar é — a₃=(0 – 8)/(7 – 5) — a₃=-4m/s² — ΔS₃=2.8/2 — ΔS₃=8m

R- B

36- I. Cálculo do deslocamento entre 0 e 8s pela área do triângulo — ΔS₁=b.h/2=8.80/2 — ΔS₁=320m — não completou a volta, pois ΔS₁ < 400m — Falsa.

II. Cálculo do deslocamento entre 0 e 9s pela soma das áreas do triângulo com a do retângulo — ΔS₂=320 + b.h=320 + 1.80 —

ΔS₂=400m — em 9s o piloto completou uma volta — Correta.

III. Entre 8s e 10s, o movimento é retilíneo e uniforme com velocidade constante de 80m/s e consequentemente a força resultante é nula — Correta.

IV. A componente da força resultante na direção do movimento é a tangencial de intensidade — FR=ma=mΔV/Δt — F_R=m.60/2 — F_R=30m — P=mg=m10 — P=10m — F_R/P=30m/10m — F_R=3p — Correta.

R- E

37- a=(V – V_o)/(t – t_o)=(-20 – 20)/(2 – 0) — a=-20m/s² — R- A

38-

-1. Correta — V_m=∆S/∆t=(600 – 200)/4 — V_m=400/4=100m/min=0,1km/(1/60)h — V_m=0,1×60=6km/h.

2. Correta — a distância não variou entre 6min e 8min, ou seja, durante 2 minutos.

3. Correta — no eixo da distância (vertical) — d=(1400 – 200)= 1200m

R- E

39-Primeira etapa — queda livre no vácuo (durante 5,0s) com velocidade variando de V_o até V , com a=g=10m/s² — V=V_o + a.t — V=0 + 10.5 — V=50m/s — durante esse tempo ele caiu uma altura h=V_ot + at²/2=0 + 10.25/2 — h=125m — observe no gráfico que no instante t=5,0s o pára-quedas abriu sua velocidade caiu instantaneamente de 50m/s para 10m/s — no intervalo de tempo (t – 5)s ele percorreu, com velocidade constante de V=10m/s a a altura h’=325 – 125=200m — V=h´/(t – 5) — 10= 200/(t – 5) — 10t – 50=200 — t=250/10 — t=25s — R- B — você poderia também resolver pela área — h_total=325=área do triângulo + área do retângulo=5.50/2 +

(t – 5).10 — t=25s.

40- Como partem juntos (instante t_o), eles se encontrarão após sofrerem o mesmo deslocamento ∆S — em todo gráfico Vxt o deslocamento é numericamente igual à área entre a reta representativa e o tempo — observe que quando o tempo é t₄ as áreas

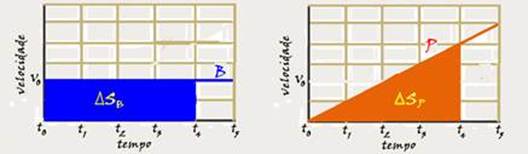
são iguais — carro B — área=∆S_B=b.h=4.2=8 unidades — carro P — área=∆S_P=b.h/2=4.4/2=8 unidades — R- D

Resoluções dos exercícios gráficos do MUV

Voltar para os exercícios