Composição de Movimentos – Resolução

Resolução comentada dos exercícios de vestibulares sobre COMPOSIÇÃO DE MOVIMENTOS

 

01- R- A  (veja teoria)

02- Veja a figura abaixo:

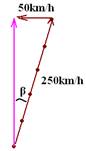
Senβ=50/250=0,2  —  β=aproximadamente 12^o  —  R-D

03- Aplicando Pitágoras no triângulo abaixo:

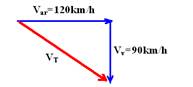
V_T²=(120)² + (90)²  —  V_T=150km/h  —  R- A

04- Ida do ninho para a árvore (contra o vento)—-  V_R=5m/s  —  V_R=ΔS/Δt  —  5=75/Δt  —  Δt=15s  —  volta da árvore para o ninho (a favor do vento)  —  V_R=15m/s  —  V_R= ΔS/Δt  —  15=75/Δt  —  Δt=5s  —  Δt_total=15 + 5  —  Δt_total=20s

05- R:

a)    b) 

06- O avião deverá estar orientado na direção sudeste, para que ele siga a rota norte-sul

 

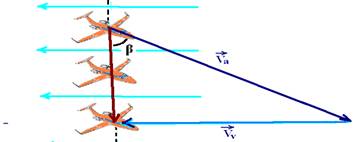
Senβ=V_v/V_a=150√3/300  —  senβ=√3/2  —  β=60^o  —  R- D

07- V_c – velocidade da caminhonete  —  velocidade do carro patrulheiro – V_p=60km/h  —  o radar do carro patrulha indica a velocidade relativa – V_r=30km/h  —  V_r=V_c – V_p  —  30=V_c – 60  —  V_c=90km/h  —  R- E

08- a) V=8 + 5  —  V=13km/h

b) V=8 – 5  —  V=3km/h

09- V_b= ΔS/Δt  —  8= 3,2Δt  —  Δt=0,4h  —  nesse tempo, devido à correnteza ele se deslocou  —  V_c= ΔS/Δt  — 

5= ΔS/0,4  —  ΔS=2km  —  chegará no ponto C.

10- V_subida= 8 – V  —  t_subida=t_s  —  V_subida=d/t_s  —  8 – V=d/t_s  —  t_s=d/(8 – V)  —  V_descida=2 + V  —  V_descida=d/t_d  —  2 + V=d/t_d  —  t_d=d/(2 + V)  —  t_s + t_d=10min  —  t_s + t_d=600  —  d/(8 – V) + d/(2 + V)=600  —  d(2 + V) + d(8 – V)=600.(8 – V).(2 + V)  —  2d + Vd + 8d – Vd = 600.(16 + 8V – 2V  – V²)  —  d=960 + 360V – 60V²  I  —  esta é uma equação do segundo grau cujo gráfico é uma parábola e da qual se quer determinar o valor máximo para d, que ocorre no vértice da parábola, de  valor V_máximo=-B/A, onde A=-60 e B=360 (veja I)  —  V_máximo=-B/A=-360/-60  —  V_máximo=3, que substituído em I, nos fornece a distância máxima percorrida  —  d_máximo=960 +360.3 – 60.3²  —  d_máximo=1500m  —  R- B

11-

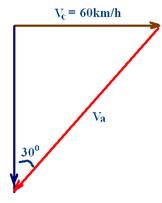
Sen30^o=V_c/V_a  —  1/2 =60/V_a  —  V_a=120km/h  —  R- C

12- d – comprimento da escada rolante  —  parado na escada  —  V_e=d/t=d/10  —  V_e=d/10  —  subindo a escada  —  V_h – V_e=d/15  —  V_h – d/10=d/15  —  V_h=d/15 + d/10  —  V_h=d/6  —  descendo a escada  —  V_h + V_e=d/t  —  d/6 + d/10=d/t  —  10dt + 6dt=60d  —  t=60/16  —  t=3,75s  —  R- B

13- Observe as figuras abaixo:

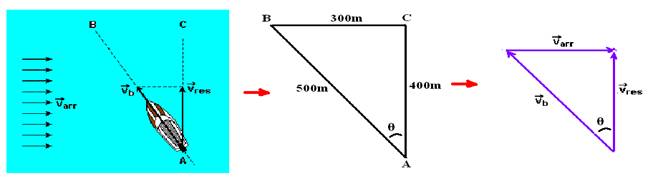
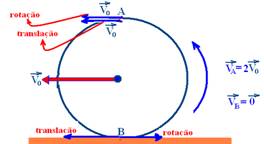
a) No triângulo ABC  —  senθ=300/500  —  senθ=0,6  —  cosθ=400/500  —  cosθ=0,8  —  na figura da direita  —  senθ=V_arr/4,5  —  0,6 =V_arr/4,5  —  V_arr=2,7m/s

b) cosθ=V_res/4,5  — 0,8=V_res/4,5  —  V_res=3,6m/s

14- R- B  (veja teoria)

15- a) veja figura abaixo

 

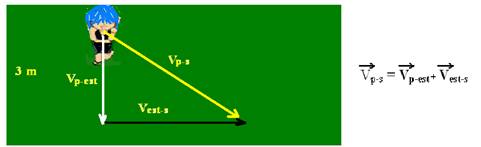
(V_p-s)² = (V_p-est)² + (V_est-s)²  —   (V_p-s)²=(1,5)²  + (2,0)²  —  V_p-s=2,5m/s

b) o tempo de travessia depende apenas da velocidade perpendicular à esteira (1,5m/s) e da largura da mesma (3m)  — 

V=ΔS/Δt  —  1,5=3/Δt  —  Δt=2s  —  substituindo esse tempo em V_p-s= ΔS/Δt  —  2,5= ΔS/2  —  ΔS=5,0m

16- Se você estiver no barco I você verá o barco II se aproximar de você e, se você estiver no barco II você verá o barco I se aproximar de você  —  R- C

17- Como a distância entre as duas bóias não varia, elas estão paradas uma em relação a outra. Então, o menino deve nadar diretamente de uma para outra  —  R- A

18- Como o observador está em repouso no navio, a distância entre ele e o navio não varia e como o pássaro voa na direção leste-oeste em relação ao navio e consequentemente à pessoa, esta o verá voando na direção leste-oeste com velocidade de 20m/s  —  R- C

19- Velocidade do barco em relação às margens  —  V_b-m=14 + 4=18km/h=18/3,6=5m/s  —  para atravessar totalmente a ponte o barco percorre ΔS=D + L=25 + 80=105m  —  V_b-m=ΔS/Δt  —  5=105/Δt  —  Δt=21s

20- Para calcular o tempo que o barco demora para atravessar o rio usa-se apenas a velocidade do barco em relação à água V_b=3,0km/h e o comprimento do rio (ΔS=1,0km)  —  V_b=ΔS/Δt  —  3=1/Δt  —  Δt=1/3h  —  Δt=20min  —  R- C

21- A favor do vento  —  V_a + V_v=180 I  —  contra o vento  —  V_a – V_v=150 II  —  resolvendo o sistema composto por I e II  —  V_a=165km/h e V_v=15km/h  —  R- A

22- V_m=240 + 260  —  V_m=500m/s  —  lembre-se que a velocidade do som independe da velocidade da fonte  —  V_s=300m/s  —  

R- D

23- A velocidade do ponto superior do cilindro que está em contato com a prancha vale 2V_Ce é igual à velocidade da prancha V_p, ou seja, V_p=2V_C

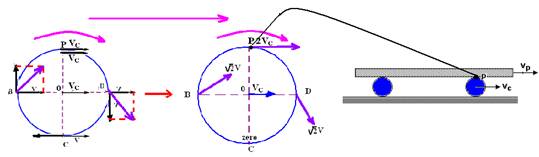
Portanto  —  V_p/V_c=2  —  R- A

24- O tempo de travessia depende apenas da largura do rio (L) e da velocidade do barco em relação às margens (u)  —  u=L/t  —  t=L/u  — quanto maior a velocidade das águas, maior será o deslocamento do barco para a direita  —  R- B

25- Subindo o rio  —  V=ΔS/Δt  —  V_b – V_a=d/10 (I)  —  descendo o rio  —  V= ΔS/Δt  —  V_b + V_a=d/4 (II)  —  fazendo (II) – (I)  —  (V_b + V_a) – (V_b – V_a)=4/4 – d/10  —  V_b + V_a – V_b + V_a = (5d – 2d)/20  —  2V_a=3d/20 (III)  —  descendo o rio com o motor desligado o barco percorre  distância d com velocidade que é a mesma que a da água V_a  — 

V_a=d/t  —  d=V_at (IV)  —  substituindo (IV) em (III)  —  2V_a=3.V_at/20  —  t=40/3=13h + 1/3h  —  t=13h e 20min  —  R- B

26- Dados: v_carro = 80 km/h; sen q = 0,8 e cos q = 0,6  —  a figura abaixo mostra o automóvel e as velocidades do automóvel

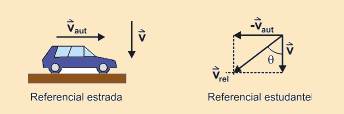
() e da chuva (), para a pessoa parada na beira da estrada. O diagrama vetorial mostra a composição dessas velocidades para o estudante  —  tg q =V_carro/V  —  senq/cosq=V_carro/V  —  0,8/0.6=80/V  —  V=60km/h  —  R- B

 

27- Dados: v_b = 11 km/h; v_a = 0,83 m/s = (0,83 ´ 3,6) = 3 km/h  —  na descida  —   v = v_b + v_a= 11 + 3 = 14 km/ h  —  na subida 

—  v = v_b – v_a = 11 – 3 = 8 km/ h  —  R- A

28- Sejam v_c a velocidade da correnteza de v_b a velocidade própria do barco  —  na descida  —  v_b + v_c = 20  (I)  —  na subida  — 

V_b – v_c = 12  (II)  —  somando as duas expressões  —  (I) + (II) Þ (v_b + v_c) + (v_b – v_c) = 32  —  2 v_b = 32  —  v_b = 16 km/h  —

Substituindo em (I)  —  16 + v_c = 20  —  v_c = 4 km/h  —  R- C

29- Como o transatlântico se move em linha reta com velocidade constante ele está em equilíbrio dinâmico e comporta-se como se estivesse em repouso (equilíbrio estático) , não afetando o movimento da bola  —  R- D  

30- Observe a figura abaixo  —  aplicando o Teorema de Pitágoras  —  130² = 50² + x²   —  x =120 m  —  da expressão

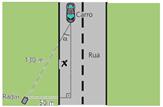
fornecida  — V_m = V_r ⋅ cos(α)  —  72=V_r.120/130  —  V_r=78km/h  —  R- C

 

31-

O tempo mínimo de travessia só ocorre quando o bote atravessa o rio com sua velocidade (V­_b=10m/s) sempre perpendicular às margens e, consequentemente perpendicular à velocidade da água (correnteza) (veja figura)  —  observe que se você utilizar apenas a

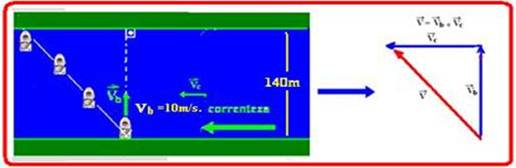
componente V_b da velocidade, a distância percorrida será a largura do rio, que é de 140m  —  V_b=∆S/∆t  —  10=140/∆t  —  ∆t=14s  —  R- D. Observação: Esse tempo não depende da velocidade da correnteza e, dependendo dela ele apenas chegará à outra margem mais próximo ou mais afastado do ponto de partida, mas o tempo de travessia será o mesmo.

32-

Trata-se de deslocamentos vetoriais cuja representação esquemática está na figura   —  observe que o triângulo é

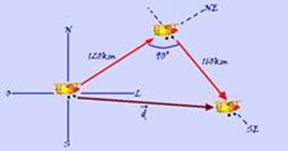
retângulo  —  Pitágoras —  d2=120² + 160²  —  d=200km  —  V_m=d/∆t=200/(1/4)  —  V_m=800km/h  —  R- E

 

 

33-

-A velocidade vetorial () do barco em relação à margem (velocidade com que uma pessoa parada na margem do rio veria o barco passar por ela), quando ele sobe o rio é fornecida por   —  observe na soma vetorial abaixo que, em módulo (intensidade)

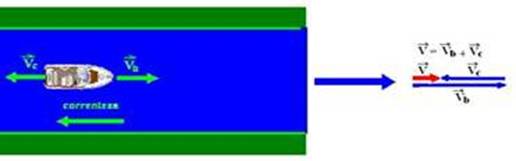
V=Vb – Vc sendo, Vb – módulo da velocidade do barco, Vc – módulo da velocidade da correnteza e V – módulo da velocidade do barco em relação à margem  —  assim, no exercício V= 13 – 5  —  V=8m/s  —  sendo a distância entre as duas cidades ∆S=40km=40.103m  —  V=∆S/∆t  —  8=40.103/∆t  —  ∆t=40.103/8=5.103 s  —  ∆t = 1h 23min 20s  —  R- B

 

Voltar para os Exercícios