Cinemática Vetorial – Resolução

Resolução comentada dos exercícios de vestibulares sobre Cinemática Vetorial

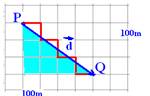
01- Aplicando Pitágoras no triângulo hachurado  —  d=500m  —  R- D

02- a) Supondo que ele se desloque no sentido anti-horário indo de M para N, o deslocamento vetorial  é obtido unindo os pontos M 

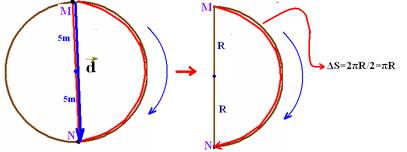
e N e a intensidade do vetor deslocamento é d=2R=2.5  —  d=10m  —  ΔS=2πR/2= πR=5π  —  ΔS=5π m

03- R- B  —  Quando um corpo sai de um ponto A, desloca-se até um ponto B, e retorna ao ponto A, mesmo que com trajetórias diferentes na ida e na volta, seu deslocamento vetorial  é nulo, pois você está somando e subtraindo dois vetores de mesma direção, mas de sentidos opostos.

04- a) A variação de espaço ΔS representa a distância efetivamente (realmente) percorrida pelo corpo (distância medida sobre a trajetória) durante o percurso de 3/4 da mesma  —   ΔS=3/4.2πR=3/4.2π.4  — ΔS=6π m  

b) O vetor deslocamento é obtido unindo-se os pontos P e Q, com sentido de P para Q

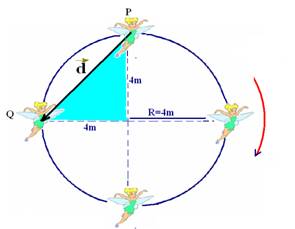
Aplicando Pitágoras no triângulo hachurado  —  d²=4² + 4²  —  d=√32  —  d=4√2 m  —  direção – oblíqua  —  sentido – sudoeste

c) V_m= ΔS/Δt=6π/2  —  V=3πm/s

d) V_m=d/Δt=4√2/2  —  V_m=2√2 m/s  —  direção – oblíqua  —  sentido – sudoeste

05- a) (NP)²=4² + 3²  —  NP=5cm  —   ΔS=MN + NP + PQ=4 + 5 + 2  —   ΔS=11cm  —  V_m= ΔS/Δt=11/2  —  V_m=5,5cm/s

b) A velocidade vetorial média  é obtida unindo M com Q e com sentido de M para Q 

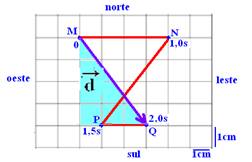
Aplicando Pitágoras no triângulo hachurado  —  d=5cm  —  V_m=d/Δt=5/2  —V_m=2,5cm/s – inclinada – sudeste

06- R- A (veja teoria)

07- Quando um corpo sai de um ponto A, desloca-se até um ponto B, e retorna ao ponto A, mesmo que com trajetórias diferentes na ida e na volta, seu deslocamento vetorial  é nulo, pois você está somando e subtraindo dois vetores de mesma direção, mas desentidos opostos. Se  é nulo, a velocidade vetorial média também é nula, pois V=d/t  —  V=0/t  —  V=0  —  R- A

08- R- E – veja resolução do exercício anterior

09- I – Observe no triângulo hachurado da figura abaixo que d=300² + 400²  —  d=500m=0,5km  —  V_m=d/t=0,5/0,5  —  V=1km/h –

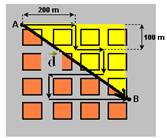
correta

II- Falsa  —  a distância percorrida vale ΔS=200 + 100 + 100 + 100 + 200 + 100 + 300  —  ΔS=1.100m

III- Correta – veja I

R- A

10- velocidade escalar  —  V_me=ΔS/Δt=6L/t  —  velocidade vetorial V_mv=d/t  —  Lcos60^o=L.12=L/2  —  V_mv=L/2 + L + L/2 + L/2 +

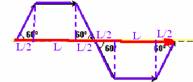
L + L/2=4L  —  V_mv=4L/t  —   t é o mesmo  —  V_me/V_mv=(6L/t)/(4L/t)  — V_me/V_mv=3/2  —  R- D

11- Se a velocidade vetorial é constante e não nula, ela tem em todos os pontos a mesma intensidade, mesma direção e mesmo sentido e, nesse caso o movimento só pode ser um  movimento retilíneo e uniforme  —  R- C

12- a) veja figura abaixo:

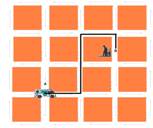
Vm=18km/h=5m/s  —  menor caminho  —  ΔS=200 + 400 + 200 + 100 =900m  —  Vm=ΔS/Δt  —  5=900/t  —  t=180s=3minutos

b) A intensidade do vetor deslocamento  é obtida aplicando Pitágoras no triângulo hachurado da figura abaixo  —  d² = 300² +

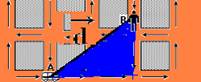
400²  —  d=500m  —  o tempo de percurso é o mesmo t=180s  —  V_mv=d/t=500/180×3,6  —  V_mv=10km/h  

13- ΔS=20 + 20 + 20 + 20 + 20  —  ΔS=100m  —  o deslocamento vetorial  é obtido unindo-se A com B, no sentido de A para B

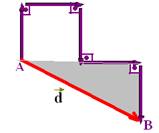
Aplicando Pitágoras no triângulo hachurado  —  d²=40² + 20²  —  d=20√5m  —  R- C

14- Como os intervalos de tempo são iguais parara todos os atletas e o deslocamento vetorial também é o mesmo (obtido, em cada caso, unindo os pontos A e B), o vetor velocidade média (V_m=d/t), também será o mesmo para todos os atletas  —  R- C

15- (01) Falsa, pois se o movimento for circular e uniforme a velocidade vetorial varia em direção e sentido.

(02) Correta – veja figuras abaixo

  

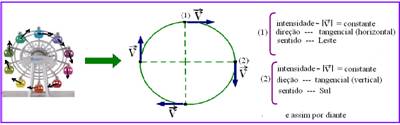
(04) Correta – todo vetor fica determinado quando se conhece sua intensidade, direção e sentido.

(08) Correta – veja (02)

(16) Falsa – veja (01)

R- soma (02 + 04 + 08)=14

16- No triângulo abaixo  —  sen30^o=cateto oposto/hipotenusa=x/d  —  1/2 = x/d   —  x=d/2  — nessas condições, o triângulo do meio

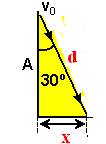
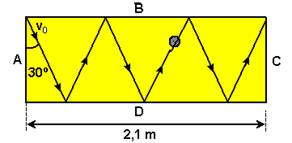
 eqüilátero de lados d  —  como tem-se 3 triângulos eqüiláteros de lados d  —  3d=2,1  —  d=0,7m – observe na figura acima que ele percorre ΔS=6d=6.0,7  —  ΔS=4,2m  —  V= ΔS/t  —  14=4,2/t  —  t=0,3s  —  t=30.10^-2s

17- Sim, pois sempre que um corpo efetua uma curva com qualquer velocidade, mesmo constante, surge sobre ele uma força que o obriga a fazer a curva (no caso a força de atrito), que é denominada força resultante centrípeta, de direção radial e dirigida para o centro da curva. Se existe força centrípeta, existirá também aceleração centrípeta também de direção radial e dirigida para o centro da curva.

18- Observe com muita atenção cada caso esquematizado na figura abaixo

 

19- Como ele está em movimento circular uniforme, a intensidade do vetor velocidade é constante e vale V=√2m/se, então não existe aceleração tangencial, mas somente centrípeta, de intensidade  —  a_c=V²/R=(√2)²/0,5=2/0,5  —  a_c=4m/s²  —  R- E

20- Se a_t=0, o movimento é uniforme e se a_c=constante e não nula ele está em trajetória circular (V e R são constantes). Portanto trata-se de um movimento circular uniforme  — R- C

21- Como a velocidade escalar V é constante, não existe a_t, somente a_c que é fornecida por a_c=V²/R  —  como V é constante, a_c é inversamente proporcional a R, ou seja, menor R – maior a_c  —  R- C

22- No movimento circular uniforme, movimento em que a intensidade (módulo) da velocidade vetorial é constante, sua direção 

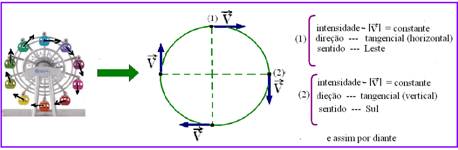
e sentido variam, poisé tangente à trajetória em cada ponto.  —  R- B

23- Se a indicação do velocímetro é constante a aceleração tangencial é nula, restando apenas a aceleração centrípeta (a_c=V²/R)  — 

1voltas completa  —  ΔS=2πR —  Δt=2min=2.60  —  Δt=120s  —  V=ΔS/Δt=2πR/120  —  V=πR/60  —  a_c=V²/R  —  4=(πR/60)²/R  —  4=π²R²/3.600 x 1/R  — 14.400=π².R  —  R=14.400/π²=14.400/9,9596=1.445,9m  —  R- D

24- I- Falsa – como a resistência do ar é desprezada, a força resultante que age sobre cada bola é seu peso (P=mg,vertical e para baixo)

II- Correta – sendo a aceleração tangencial constante (a_t=g), a maior altura será atingida por aquela que tem maior velocidade inicial.

III_ Correta – pela aceleração da gravidade g, vertical e para baixo

R- D

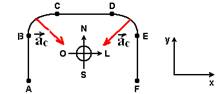
25- I- no trecho AB é acelerado com a_t, pois partiu do repouso V_o=0  —  nos trechos BC e DE, não tem a_t (velocidade constante) mas tem a_c (trajetória curva)  —  no trecho EF é retardado com a_t, pois está freando até parar  —  correta  

II- correta – num trecho ele acelera e no outro, retarda.

III- correta – veja figura abaixo

R- E

26- O vetor velocidade é tangente à trajetória e tem o sentido do movimento (horizontal e para a direita)  —  a aceleração centrípeta é dirigida para o centro da curva (vertical e para baixo)  —  R- e 

27- De acordo com o enunciado a_t=1m/s²  —  V após 10s vale V=V_o + at  —  V= 0 + 1.10  —  V=10m/s  —  a_c=V²/R=10²/100  —  a_c=1m/s²

28- Observe a figura abaixo

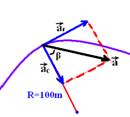
a²=1² + 1²   —  a=√2m/s²  —  senβ=a_t/a  —  senβ=1/√2  —  senβ=√2/2  —  β=45^o  —  R- D

29-  Movimento uniforme  —  —   e  são perpendiculares   —  R- C

30- Entre 2s e 4s ele percorreu um quarto do arco da circunferência  —  ΔS=2πR/4  —  V= ΔS/Δt  —  √2=(πR/2)/(4-2)  —  4√2=πR  —  R=4√2/π  —  R= 1,8m  —  sendo a velocidade constante só existe aceleração centrípeta, também constante  —  a_c=V²/R  — 

a_c= (√2)²/1,9=1,0m/s²  —  R- C

31- Somente na trajetória II, onde existe aceleração centrípeta e consequentemente força centrípeta e, pelo princípio da inércia ele se “sentirá jogado”, em sentido contrário ao da curva, tentando sair pela tangente  —  R- B

32- Na figura abaixo a aceleração  está decomposta em suas parcelas  e 

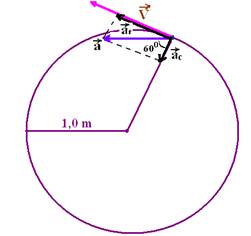
cos60^o=a_c/a  —  0,5=a_c/32  —  a_c=16m/s²  —  a_c=V²/R  —  16=V²/1  —  V=4m/s  — R- B

33- Veja esquema abaixo:

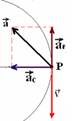R- D

34- R- B  (veja teoria)

35- Se está em MCU, a aceleração tangencial é nula, a velocidade vetorial é tangente e a aceleração é a centrípeta  —  R- D

36- R- C  —  está em movimento circular uniforme

37- A figura abaixo mostra os vetores  e , decompostos a partir do vetor .

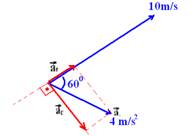
sen60^o=a_c/4  —  0,87=a_c/4  —  a_c=3,48m/s²  —  a_c=V²/R  —  3,48=(10)²/R  —  R=29m  —  cos60^o=a_t/4  —  0,50=a_t/4  —  a_t=2,0m/s²  —  R- D

38-

Veja figura abaixo

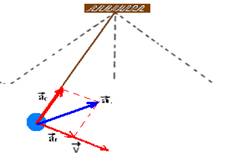
R- D

39– Trata-se de uma localização em três dimensões

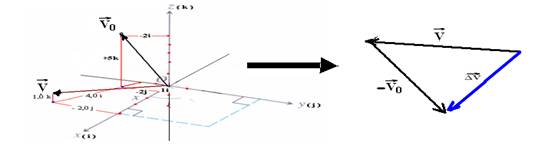
ΔV=V – V₀=(4i – 2j + k) – (i -2j + 5k) = 4i -2j +k –i +2j – 5k  —  ΔV=3i – 4k  —  a= ΔV/Δt=(3i – 4k)/2  —  a=1,5i – 2k

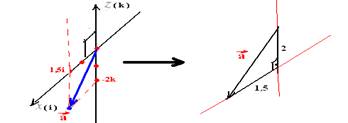
a²=(1,5)² + (2,0)²  —  a=√6,25  —  a=2,5m/s²  —  R- D

40- a) Como CI parte de A e PA parte de B, o deslocamento de CI deve ser 300m maior que o deslocamento de PA  — ΔS_CI=ΔS_PA +300  —  como o movimento de CI é uniformemente variado e o de PA é uniforme  —  equações de cada um com a origem em A  —  ΔS_CI=gt²/2  —  ΔS_PA=Vt + 300  —  no encontro  —  ΔS_CI=ΔS_PA  —  5.10^-3t²/2=1.t + 300  —  2,5.10^-3t² – t + 300=0  —  resolvendo a equação  —  t=600s (tempo do encontro)  —  deslocamento escalar de PA  —  ΔS_PA=Vt=1.600  —  ΔS_PA=600m  — como PA percorreu 600m até o encontro, ele ocorre no ponto D da figura abaixo  —  a diagonal do quadrado (BD) é o

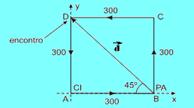
deslocamento vetorial () de PA e tem intensidade   —  d=300√2m  —  o vetor velocidade média () tem intensidade  —  V_m=300√2/600  —  V_m ≈ 0,7m/s, direção  —  oblíqua  —  sentido  —   NO formando um ângulo de 45^o com a horizontal.

b) CI andará 900m até o encontro  —  V_m=900/600  —  V_m=1,5m/s

 

41- Cálculo do deslocamento em todo o trajeto DS = v.Dt = 24.1 = 24 km  —  distância AB pode ser calculada da seguinte forma  — DS = 2.AB + 2.BC  —  DS/2 = AB + BC  —  AB = DS/2 – BC =24/2– 3 = 12 – 3 = 9 km  —   tempo total gasto no trecho ABCB

v = DS/Dt  —  Dt = DS/v = (9 + 6)/20= 15/20  —  Dt = 0,75 h  —   módulo da velocidade vetorial média 9/0,75 = 12 km/h

R- A

42- Dados  —  largura do rio D = 60 m  —   Dt = 2 min = 120 s  —  cos q = 4/5  —  sen q =3/5  —  a figura abaixo ilustra as

velocidades, sendo: v a velocidade de Pedro em relação à margem; V_p/ag: a velocidade de Pedro em relação à água e v_ag a velocidade da água.

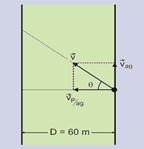
a) V_p/ag=D/Δt=60/120  —  V_p/ag=0,5m/s 

b) Da figura  —  cosθ= V_p/ag/V  —  3/5=0,5/V  —  V=2,5/3  —  V=0,83m/s

c) Da mesma figura  —  senθ=V_ag/V  —  4/5=V_ag/2,5/3  —  V_ag=10/15  —  V_ag=0,67m/s

 

43- O vetor deslocamento () do carteiro é obtido unindo-se os pontos A com B, figura abaixo  —  o módulo de  é fornecido pelo teorema de Pitágoras  —  d²=400² + 300²  —  d=500m  —  direção oeste-leste  —  sentido para o leste  —  R- C

44- Distância percorrida do sul para o norte  —  V=ΔS/Δt  —  20=ΔS/(15/60)  —  ΔS=5km  —  o novo deslocamento de 5km forma um ângulo de 60^o com o deslocamento inicial  —  veja a figura abaixo onde  é o vetor deslocamento pedido  —  aplicando a

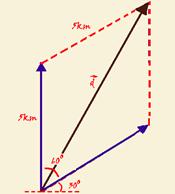
lei dos cossenos  —  d²=5² + 5²  + 2.5.5.cos60^o  —  d=√75  —  d=5√3m

 

45-

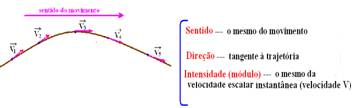
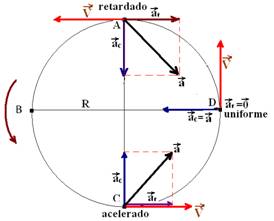
A aceleração vetorial  é definida como , e indica a variação de velocidade uma unidade de tempo  sendo que essa variação pode acontecer tanto em direção como em sentido.

Assim, a aceleração vetorial  pode ser decomposta em duas; a aceleração tangencial  e a aceleração centrípeta , conforme a figura.

 Características da aceleração tangencial (): é responsável pela variação da intensidade (módulo) do vetor velocidade, fazendo com que o movimento seja acelerado ou retardado.

R- A

 

 

46-

Em qualquer movimento circular (uniforme ou não) surge sempre uma aceleração denominada aceleração centrípeta  responsável pela variação da direção do vetor velocidade,com as seguintes características:  

R- B

 

47-

Em todo movimento circular existe sempre uma força resultante com direção radial e sentido dirigido para o centro da circunferência, de intensidade Fc=mV2/R, denominada força resultante centrípeta  —  R- C

 

Voltar para os Exercícios