Movimento acelerado e movimento retardado – aceleração média
Resoluções – Movimento acelerado e movimento retardado – aceleração média
01- am=(V – Vo)/(t – to) — am=(72/3,6 – 0)/(2 – 0) — am=10m/s2
02- I- a1=(2v – v)/t — a1=v/t — II – a2=(3v – v)/2t — a2=v/t — III – a3=(5v – v)/5t — a3=4v/5t — R- D
03- am=(0 – 20)/(4 – 0) — am=-5m/s2 — R- C
04-am=(V – Vo)/(t – to) — 2=(108/3,6 – 0)/(t ) — 2=30/(t ) — t=15s
05- Orientando a trajetória, antes de rebater velocidade positiva e depois de rebater, velocidade negativa:
Am=(-30 – 20)/0,1 — am=-50/0,1 — am=-500m/s2 — R- D
06- R- B
07- Menor tempo – maior aceleração – Corvette — am=100/4=25(km/h)/s — maior tempo – menor aceleração – Parati —- am=100/33,35=3(km/h)/s — R- C
08- Entre 3s e 9s — am=(0 – 12)/(9 -3) — am=-12/6 — am=-2m/s2 — entre 0 e 12s — am=(-12 – 6)/(12 – 0) — am=-18/12 — am=- 1,5m/s
09- a=(2 – 0)/(4 – 0) — a=1/2m/s2 — R- B
10- Observe que até 3s a aceleração é constante e vale 3m/s2 (terreno mais inclinado) e que depois ela cai para 2m/s2 (terreno menos inclinado) — R- C
11- Trecho AB — progressivo (V>0) e retardado (o módulo de V está diminuindo, ele vai parar em B “VB=0”)
Trecho BC — retrógrado (V<0) e acelerado (módulo de V está aumentando “em B estava parado”)
Trecho CD — Movimento uniforme com velocidade constante e negativa, portanto retrógrado mas sem aceleração.
Trecho DE — retrógrado (V<0) e retardado (módulo de V está diminuindo “pára em E”)
Trecho EF — progressivo (V>0) e acelerado (módulo de V está aumentando “saiu do repouso em E”)
12- R- C — entre t2 e t3 0 movimento é retrógrado (velocidade negativa) e acelerado (módulo da velocidade está aumentando “estava parado em t2”)
13- a) entre 6s e 16s, a velocidade é constante e a aceleração é nula.
b) entre 0 e 6s (movimento progressivo acelerado)
c) o deslocamento (distância percorrida) em todo gráfico V X t é fornecido pela área entre 0 e 20s — área do triângulo=b.h/2=6.12/2=36m + área do retângulo=b.h=10.12=120m + área do trapézio=(B + b).h/2=(12 + 10).4/2=44m — deslocamento = 36 + 120 + 44 — d=200m
d) Vm=d/t — Vm=200/20 — Vm=10m/s
14- a) V=90/3,6=25m/s
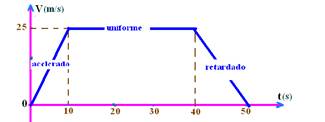
b) A distância é fornecida pela área do trapézio — ΔS=(B + b).h/2=(50 + 30).25/2 — ΔS=1.000m
15- Se o movimento for progressivo o sinal será positivo, mas se o movimento for retrógrado o sinal será negativo.
16- (01) Correta — V é constante e vale 12m/s X 3.6=43,2km/h e o movimento é progressivo (V>0 e a=0)
(02) Falsa — o movimento é uniformemente acelerado mas a aceleração vale a=(20 – 12)/(25 – 10) — a=0,53m/s2
(04) O deslocamento é fornecido pela área do trapézio — ΔS=(20 + 12).15/2 — ΔS=240m — Correta
(08) ΔS=10t=10.10=100m — entre 0 e 10s ΔS é fornecido pela área do retângulo=10.12=120m — Falsa
(16) Falsa — nada se pode afirmar a respeito da trajetória
Soma=(01 + 04) = 05
17- Quanto mais inclinada reta representativa da velocidade maior será a aceleração — R- A
18- R- C — é o único movimento que é retardado com a velocidade diminuindo até que ele pare.
19- R- D
20- Movimento progressivo (indo), ΔS=área do trapézio=(2 + 1).2/2=3m que é a mesma que do movimento retrógrado (voltando) — R- C
21- Observe no enunciado que ele começou a reduzir a velocidade de 360kmh para 270kmh quando apagou — movimento retardado com velocidade diminuendo — R- C
22- Entre 0 e 6s — VI=Vo + aItI=2 + 4.6 — Vi=26 cm/s — entre 6s e 10s — VI=Vo=26cm/s — VII=Vo + aIItII=26 + (-3).4 — VII=14 cm/s — VII=Vo=14 cm/s — VIII=Vo + aIII.tIII=14 + 4.6 — VIII=38 cm/s
23- a) Supondo que nos intervalos de 0 e 4 s e de 12 s a 16 s a velocidade permaneça constante e que, nos intervalos de 4 s a 8 s e de 16 s a 20 s as variações de velocidade sejam constantes, o gráfico pedido está representado abaixo.
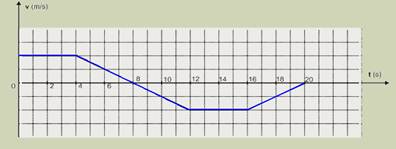
b) Com base no gráfico obtido no item( a) podemos descrever o movimento do carrinho da seguinte maneira:
de t = 0 a t = 4 s o movimento é progressivo e uniforme;
de t = 4 s a t = 8 s o movimento é progressivo e uniformemente retardado;
de t = 8 s a t = 12 s o movimento é retrógrado e uniformemente acelerado;
de t = 12 s a t = 16 s o movimento é retrógrado e uniforme,
de t = 16 s a t = 20 s o movimento é retrógrado e uniformemente retardado.
24- Sendo a trajetória é retilínea, a aceleração restringe-se à componente tangencial 
, que, em módulo, é igual a aceleração escalar (a), dada pela taxa de variação da velocidade (Dv) em relação ao tempo (Dt) — a=ΔV/Δt — para cada intervalo você tem — I. aI=(40 – 0)/(4 – 0) — aI=10m/s2 — II. AII = 0 (não houve variação de velocidade) — III. aIII=(0 – 40)/(14 – 6) —
aIII= – 5m/s2 — R- C
25- am=ΔV/Δt — como ΔV1=2 ΔV2 — am1=2am2 — R- D
26- Cálculo da aceleração de retardamento do carro — Vo=54km/h/3,6=15m/s — V=0 (pára) — t=5s — V= Vo + a.t — 0
= 15 + a.5 — a= – 3m/s2 (o sinal negativo de a significa que o carro está freando) — em módulo — a=3m/s2 — depois que ele acionou os freios a intensidade da força resultante sobre o carro é a própria força de atrito — FR=Fat — m.a = μ.N — m.a = μ.m.g — 3= μ.10 —
μ = 0,3 — R- A