Sistemas de Unidades – Análise dimensional

– Quando você está estudando um determinado fenômeno, você analisa as variáveis que participam do mesmo de modo que elas forneçam dados relevantes sobre o mesmo. Estas variáveis se denominam grandezas físicas que correspondem a tudo que você pode contar, medir, pesar, enfim, enumerar..

– Escolhida a grandeza física a ser analisada no fenômeno você deve medi-la o que significa compará-la com outra de mesma natureza, ou seja, com um padrão denominado unidade. Assim, a medição é a técnica por meio da qual você atribui um número a uma grandeza física e, para avaliá-la, você deve compará-la com outra similar tomada como padrão, denominada unidade.

Exemplo: O jovem da figura está medindo sua massa (48kg) e sua altura (1,5m) onde massa e altura são, respectivamente, as grandezas físicas, 48 e 1,5 os números e kg e m os nomes das unidades empregadas.

– Por muito tempo, o mundo usou medidas imprecisas, como aquelas baseadas no corpo humano: palmo, pé, polegada, braça, côvado. Isso acabou gerando muitos problemas, principalmente no comércio, devido à falta de um padrão para determinar quantidades de produtos.

Por esse motivo a Academia de Ciência da França, em 1789, criou um sistema de medidas baseada numa constante padrão e não arbitrária denominado Sistema Métrico Decimal que era formado inicialmente por três unidades fundamentais básicas: o metro, o litro e o quilograma.

– Atualmente o metro é definido como sendo o comprimento do trajeto percorrido pela luz no vácuo, durante um intervalo de tempo de 1/299.792.458 de segundo; o quilograma corresponde a massa de um modelo internacional de platina iridiada (feito de iridio e platina) que se encontra conservado no Escritório Internacional de Pesos e Medidas (BIPM), situado no parque de Sant Cloud, nas proximidades de Paris (França). Um litro corresponde ao volume interno de um recipiente em forma de cubo com 1dm de aresta (1L=1dm³).

Sistema Internaconal de Unidades (SI)

– Com o decorrer do tempo, com as relações comerciais entre os países aumentando foi necessário obter um sistema de unidades mais abrangente, útil e complexo, o Sistema Internacional de Unidades (SI) que, no Brasil, foi adotado em 1962 sendo posteriormente, em 1998 ratificado pelo CONMETRO que tornou seu uso obrigatório em todo Brasil. Nela constam as sete grandezas de base adotadas pela Organização Internacional de Normatização (ISO) que são: comprimento, massa , tempo, corrente elétrica, temperatura termodinâmica, quantidade de matéria e intensidade luminosa.

– A Organização Internacional de Normatização (ISO), adotou um sistema de grandezas físicas baseado nas sete grandezas de base: comprimento, massa , tempo, corrente elétrica, temperatura termodinâmica, quantidade de matéria e intensidade luminosa.

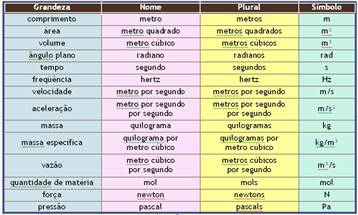
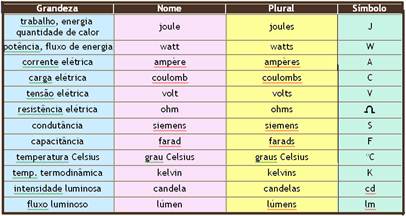
A tabela a seguir mostra as grandezas do SI, nome das unidades, plural das mesmas e os respectivos símbolos:

Unidades derivadas

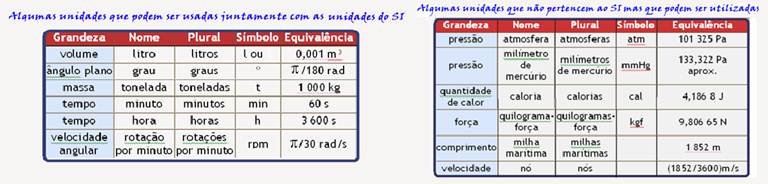
– Consideram-se unidades derivadas do SI apenas aquelas que podem ser expressas através das unidades básicas do SI e sem sinais de multiplicação e divisão, ou seja, sem qualquer fator multiplicativo ou prefixo com a mesma função. Desse modo, há apenas uma unidade do SI para cada grandeza. Contudo, para cada unidade do SI pode haver várias grandezas. Às vezes, dão-se nomes especiais para as unidades derivadas. Observe a tabela abaixo:

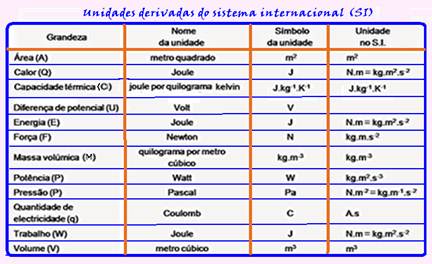
Regras para se escrever unidades do SI

– Os nomes das unidades do SI devem ser escritos em letra minúscula, mesmo sendo nomes de pessoas — exedmplos: quilograma; newton, metro quadrado, kelvin, etc — são duas as exceções – no início da frase – grau Célsius

– Escrevendo os nomes no plural — os nomes das unidades do SI não coincidem com as regras da gramaticais — veja a primeira tabela acima.

– Escrevendo os símbolos das unidades — o acento tônico recai sobre a unidade e não sobre o prefixo — exemplos: megametro; hectolitro;centigrama; micrometro — exceções: quilômetro; decâmetro; hectômetro; decímetro; centímetro e milímetro.

– Nenhum símbolo deve ser seguido de ponto — exemplo: hora – correto – (h) — errado (h.;hr.); — segundo – correto (s) – errado (s.;seg.); — metro – correto (m) – errado (m.;mtr.;mt.); — minuto – correto – (min) – errado – (min.; minut.); — quilograma – correto (kg) – errado (kg.;kgr.).

– O símbolo das unidades SI é invarável e, no plural não deve ser seguido de “s” — exemplos: doze horas – (12h e não 12 hs); 5 minutos – (5 min e não 5mins); 6metros – (6m e não 6ms).

– Quando você for escrever uma unidade composta não misture nome com símbolo — exemplos: metro por segundo ao quadrado e não metro/s²; km/h e não km/hora.

– O grama é de gênero masculino e, portanto, você deve escrever fazendo a concordância de forma correta — exemplos: seis quilogramas; oito miligramas; duzentos e vinte e um gramas.

– O prefixo quilo deve ser escrito de maneira correta — exemplos: quilolitro e não kilolitro; quilômetro e não kilômetro; quilograma e não kilograma.

– Nas medidas de tempo você deve escrever os símbolos da maneira correta — exemplos: 5h20min e não 5,20h ou 5h 20’; 2h24min5s e não 2h24’5’’ — observação: os símbolos (’) e (’ ’) são unidades de ângulo plano e não de tempo.

Análise Dimensional

– A análise dimensional no campo da física está relacionada com as unidades de medida das grandezas físicas e é útil na resolução de equações que relacionam essas grandezas físicas. Ela facilita a memorização das equações matemáticas dos fenômenos físicos.

– Qualquer equação matemática que representa uma situação física qualquer precisa, além de um número que a quantifique de uma unidade de medida que faça a classificação qualitativa.

– Todas as grandezas físicas podem ser analisadas dimensionalmente através de três unidades que você deve tomar como parâmetros que são: Comprimento (L), Tempo (T) e massa (M). As outras unidades de medidas de grandezas derivadas terão suas unidades de medidas provenientes dessas três. Costuma-se adotar as grandezas fundamentais do S.I. para se escreverem as equações dimensionais.

– Uma grandeza dimensional é representada por colchetes e você pode expressa-la em função das grandezas fundamentais. Por exemplo, uma grandeza física (F), que depende da massa, do comprimento e do tempo, tem sua equação dimensional escrita da seguinte maneira:

Os números a, b e c são chamados de dimensões da grandeza G. Por definição, a grandeza F possui dimensão a em relação à massa M, dimensão b em relação ao comprimento L e dimensão c em relação ao tempo T.

– Observação: Uma grandeza é dita adimensional se ela é desprovida de unidades, ou seja, o resultado final da dimensão é

unitário. Exemplo: a grandeza G é uma grandeza adimensional se G=v.t/∆S, sendo v a velocidade,, t o tempo e ∆S o comprimento. Assim [G] =(m/s)t/∆S= (L/T).T/L=L.T^-1 .T .L^-1 — [G] = 1

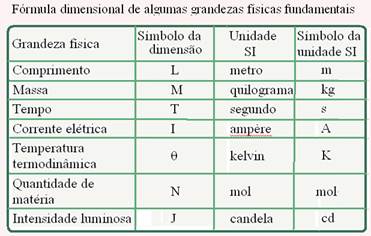
– Consideram-se unidades derivadas do SI apenas aquelas que podem ser expressas através das unidades básicas (fundamentais) do SI, expressas na tabela acima.

– Exemplos de como proceder no cálculo das dimensões de uma grandeza dimensional derivada ou de uma grandeza expressa por uma função matemática:

01- Calcule a fórmula dimensional das seguintes grandezas físicas derivadas:

Peso – Newton

peso é força — P=mg=kg.m/s² — [P]=M.L.T^-2

Pressão – Pascal

P_r=dgh=(kg/m³).(m/s²).(m) — [P_r]=(ML^-3).(L.T^-2).(L) — [P_r]=M.L^-1.T^-2 ou [P_r]=F/S=(ma)/S=(kg).(m/s²)/m² — [P_r]=(M).(L.T^-2).(L^-2) — [P_r]=M.L^-1.T^-2

Energia – Joule

Trabalho é variação de energia — W=F.d=mad=(kg).(m/s²).m — [W]=(M).(L.T^-2).L — [W]=M.L².T^-2

02- Segundo Einstein, uma luz de frequência n pode ser considerada como sendo constituída de fótons, partículas com massa em

repouso nula e com energia E=hn, sendo h a constante de Planck. Calcule a dimensão da constante h.

E=hn — h=E/n=F.d/1/T=m.a.d.T^-1=kg.m/s².m.s^-1 — h=kg.m².s^-1 — [h]=M.L².T^-1

Se uma equação que traduz uma lei física é homogênea, as parcelas que constituem os dois membros da igualdade fornecem os

mesmos símbolos dimensionais. Assim , na expressão da energia relativística de Einstein E=m_o.c², onde E representa a energia relativística da partícula em repouso, m_o a massa de repouso da partícula e c a velocidade da luz no vácuo, as unidades dimensionais de E e de m_o.c²devem ser iguais. Prove essa igualdade.

E = energia de repouso — [E] = J = N.m = (kg.m/s²).m = kg.m²/s² — [E] = M.L².T^-2 — [ m_o]=kg=M — c=m/s — c²=(m/s)²=m².s^-2 — [c²]=L².T^-2 — [ m.c²]=M.L².T^-2 — portanto E e m.c² possuem símbolos dimensionalmente iguais e são homogêneas.

Fórmulas dimensionais de algumas grandezas físicas derivadas