Resolução comentada dos exercícios de vestibulares sobre
Trabalho de um gás – Transformações cíclicas
01- R- C — veja teoria
02- W=P.ΔV — 30=P(5 – 2) — P=10N/m2(Pa) — R- A
03- 1g – 5.103cal — 4.000g – Q cal — Q=2.107cal — 1cal – 4,2J — 2.107cal – W J — W=8,4.107J — rendimento de 15% — Wútil=0,15.8,4.107=1,26.107 J — R- E
04- Trata-se de uma transformação de calor (gerado pela queima do combustível) em trabalho (movimentação do veículo) —
R- A
05- a) WAB=área do triângulo=b.h/2=10.10/2 — WAB=50 J
b) WBC=área do retângulo=b.h=(20 – 10).10 — WBC=100 J
c) WCD= zero
d) WAD=50 + 100 + 0 — WAD=150 J
06- Observe que o menor trabalho corresponde à menor área, que é a hachurada na figura abaixo —
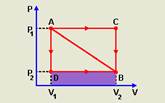
W=área do retângulo=b.h — W=(V2 – V1).P2 — R- B
07- Trecho CD — WCD=P.ΔV=P.(VD – VC)=5,8.(0,8 – 1,6) — WCD= – 4,64 J — R- A
08- O trabalho no trecho AB é numericamente igual à área do trapézio, hachurada na figura, e de
valor W=(B + b).h/2=(30.104 +10.104).20.10-2/2/2 — W=400.102J=40.103J — W=40kJ — R- C
09- Observe as áreas que fornecem os respectivos trabalhos:
R- D
10- a) De A para B — isovolumétrica — PA/TA=PB/TB — 5/TA=2/TB — TA=5/2TB (I) — de B para C — isobárica — VB/TB=VC/TC — 2/TB=5/TC — TB=2/5TC (II) — comparando I com II — TA=TC ou TA/TC=1
b) Trabalho pela área — WAB=0 — WBC=P.(VC – VB)=2(5 – 2) — WBC=6J — Wtotal= 0 + 6 — Wtotal=6J
11– W=P.ΔV — 30=P(5 – 2) — P=10N/m2(Pa) — R- A
12- a) V=S.h=500.20=103 cm3 — V=104.10-6 — V=10-2 m3 — PV=nRT — (105 + 10m/5.10-2).10-2 = 0,5.8.300 — 103 + 2m=1,2.103 — m=102kg
b) isobárica — Vo/To=V/T — S.0,2/300=S.h/420 — h=0,28m — W=P.ΔV=1,0.105.5.10-2.(0,28 – 0,20) — W=400J
13- Volume da caixa — V=ℓ3=(4.10-2)3 — V=64.10-6m3 — área de cada parede — S=ℓ2=(4.10-2)2 — S=16.10-4m2 — a 300K — pressão nas paredes — P=1atm=105N/m2 — P=F1/S — 105=F1 /16.10-4 — F1=160N — a 330K — cálculo da pressão no final desta transformação que é isovolumétrica — Po/To=P/T — 105/300=P/330 — P=1,1.105N/m2 — P=F2/S — 1,1.105=F2/16.10-4 — F2=176N — ΔF=F2 – F1=176 – 160 — ΔF=16N
14- Antes — Pa=Patm=1atm=105N/m2 — Va=S.h=20.10-4.1 — Va=2.10-3m3 — depois — Pd=Patm + P=P + 105 — Vd=S.h — Vd=20.10-4..0,8 — Vd=1,6.10-3m3 — isotérmica — PaVa=Pd.Vd — 105.2.10-3=(P + 105).1,6.10-3 — P=25.103N/m2 — na situação depois, a pressão com que o êmbolo comprime o gás vale — pressão=força/área=peso/área — 25.103=peso/20.10-4 —
peso=50N — peso=m.g — 50=m.10 — m=5,0kg
15– R- B — veja teoria e lembre-se de que nesse caso o trabalho é negativo (sentido anti-horário).
16- Como a transformação cíclica é no sentido horário, o trabalho realizado é positivo (predomina a expansão – do gás sobre o ambiente) e fornecido pela área do ciclo — W=base x altura=((0,3 – 0,1).(30 – 10) — W= + 4J — R- B
17- W positivo – sentido horário — W=(5 – 2).(800 – 300) — W= + 1.500J — R- A
18- O trabalho é positivo – sentido horário — área do paralelogramo=base x altura — W=(6Vo – 2Vo).(P2 – P1) — W=4Vo.(P2 – P1)
19- A temperatura mais alta corresponde ao ponto cuja isoterma se encontra mais afastada dos
eixos (ponto B) conforme a figura e o trabalho é positivo (sentido horário) e de valor — W=(4.10-6 – 1,5.10-6).(4.105 – 2.105)=2,5.10-6.2.105 — W= +5.10-1J —
R- A
20-
Wtotal=W1 + W2=b1.h1 + b2.h2=(4 – 1).(1) + (7 – 4).(2 – 1)=3 + 3 — Wtotal= 6J — R- D
21– W=b.h/2=(6.10-6-2.10-6).(3.105 – 1.105)/2 — W=4,0.10-1J — R- B
22– Em toda transformação cíclica o trabalho realizado é numericamente igual à área interna do ciclo — observe na figura que a menor área é a do ciclo K (menor que quatro quadrículos) — R- C
23- a) d=m/V — Vo=60,1,2 — Vo=50m3
b) Equação geral dos gases perfeitos — Po.Vo/To = P.V/T — 50/300 = V/500 — V=250/3 — V=83,3 m3 (V>Vo o gás sofreu expansão)
c) Expansão isobárica — W=P.(V – Vo)=105.(83,3 – 50) — W=33,3.105=3,3.106 J
24– Em um ciclo fechado o trabalho é numericamente igual à área da figura. Seu valor é negativo devido ao sentido anti-horário.
R- E
25-
I. Verdadeira — observe que o processo de 1 para 2 ocorre à volume constante e que o de 3 para 1 ocorre à pressão constante.
II. Falsa — observe que nesse processo o volume não varia (∆V=0) e, como W=P.∆V, W=0.
III. Verdadeira — nesse processo o trabalho é negativo, pois o volume está diminuindo e o meio exterior exerce W sobre o gás.
IV. Verdadeira — do enunciado — P2=5P1 — todos os pontos da mesma curva da isoterma possuem a mesma temperatura — T2=T3 — o processo de 1 para 2 é uma isovolumétrica e seu volume não varia (V1=V2=V) — P1.V/T1 = P2.V/T2 — P1/T1=P2/T2 — P1/T1=5P1/T2 — T2=5T1 — como T2=T3 — T3=5T1.
V. Verdadeira — em todo ciclo a temperatura final e inicial são iguais e, consequentemente não ocorre variação da energia interna do sistema.
R- E.
26- Neste ciclo você tem — Trecho AB — isotérmica de expansão — trecho BC — isocórica ou
isovolumétrica — trecho CD — isotérmica de compressão — Trecho DA — isocórica ou isovolumétrica.
As respostas devem ser em função dos dados fornecidos, ou seja, em função de PA, VA, PC e VC.
Primeira linha — no trecho AB trata-se de uma isotérmica (mesma temperatura TA=TB=T) — PA.VA/T=PBVB/T ou PA.VA=PB.VB = constante — equação dos gases perfeitos — PA.VA=nRTA — TA=TB=T=PA.VA/nR (I) — P=PA(dado); V=VA (dado) e T=PA.VA/nR —segunda linha — no trecho BC
trata-se de uma isocórica ou isovolumétrica (volume constante VB=VC=V) — do trecho AB — PA.VA=PB.VB (II) — do trecho BC (III) — VB=VC — (III) em (II) — PA.VA=PB.VC — PB=PA.VA/VC — P= PA.VA/VC; V=VC e T= PA.VA/nR (de I) — terceira linha — isotérmica — TC=TD — equação dos gases ideais — PC.VC=nRTC — TC=PC.VC/nR — P=PC; V=VC e T= PC.VC/nR — quarta linha — analogamente — P=PC.VC/VA, V=VA e T= PC.VC/nR.
b) * Transformação isotérmica — como a temperatura (T) e a energia interna (U) de um sistema estão associadas à energia cinética das moléculas, se a temperatura for constante, a energia interna (U) do sistema também será constante. Assim, a variação
de energia interna (ΔU) do sistema será nula — ΔU=0 — ΔU= Q – W — 0=Q – W — Q=W — portanto em toda transformação isotérmica todo calor Q recebido pelo sistema ou cedido por ele é transformado em trabalho W.
* Transformação isocórica, isométrica ou isovolumétrica — ocorre a volume constante — Vo=V —
ΔV=0 — W=P.ΔV — W=P.0 — W=0 — ΔU = Q – W — ΔU=Q – 0 — ΔU=Q — assim, todo o calor (Q) recebido pelo sistema é igual à sua variação de energia interna (ΔU)
Primeira linha — isotérmica — ΔU=0 — Q=W — Q=300J — W=Q=300J — segunda linha —
isocórica — W=0 — ΔU=Q —ΔU= -750J — Q= – 750J — terceira linha — isotérmica — ∆U=0 — Q=W — W = -150J — Q= – 150J — quarta linha — isocórica — W=0 — ∆U=Q — Q=750J — ∆U=750J.