Resolução comentada dos exercícios de vestibulares sobre Tipos de transformações gasosas
Resolução comentada dos exercícios de vestibulares sobre
Tipos de transformações gasosas
01– R- D — veja teoria
02- Isotérmica — P.V=constante — P é inversa a V — R- D
03- R- B — veja teoria
04- R- A — veja teoria
05- Observe que a pressão sobre o êmbolo é constante, pressão atmosférica que é constante mais a pressão devido ao peso, que também é constante. Assim trata-se de uma transformação isobárica onde o gás se expande com aumento de temperatura — R- B
06- Trata-se de uma transformação isotérmica — P.V=constante — inversamente proporcionais — se você dobra a pressão, o volume cai pela metade — massa específica — μ=m/V — μ e V são inversamente proporcionais — se V cai pela metade, a massa específica μ duplicará — R- B
07- Trata-se de uma transformação isotérmica — P.V=K — (V=1, P=2) — 2.1=K — R- D
08- Isotérmica — Po.Vo=P.V — Po.1=0,9Po.V — V=1/0,9 — V=1,111 — R- D
09- Po.Vo/To=P.V/T — (3P/2).Vo/0,93.T=P.V/T — 3Vo/1,86=V/1 — Vo/V=1,86/3 — Vo/V=0,62
10- Observe que a primeira transformação o gás recebe calor e sua temperatura e volume aumentam sob pressão constante (pressão atmosférica + pressão devido ao peso do êmbolo), portanto trata-se de uma transformação à pressão constante (isobárica) — na segunda transformação o gás está em equilíbrio térmico com o ambiente tendo a mesma temperatura que ele (isotérmica) —R- A
11- Devido à redução da pressão externa o volume do balão aumenta para que ocorra redução da pressão interna — R- C
12- R- (1 + 2 + 8) = 11
13- Como a temperatura de ebulição é crescente, com o aumento de pressão máxima o único diagrama que representa isto é o II.
14- Po.Vo/To=P.V/T — PoVo/To=P.(6/5)Vo/(9/10)To — Po.Vo/To=(P.6Vo)/5 x 10/(9To) — Po=60P/45 — P=3/4Po — R- B
15- A transformação é isotérmica com diminuição da pressão e aumento de volume — R- D
16- a) Observe na última coluna que o produto PxV é praticamente constante (Lei de Boyle para transformações isotérmicas)
b) Supondo que cada 8 unidades tenha 0,5cm — regra de três — 8u – 0,5m — 24u – h — h=1,5m — P=Po + dgh=1,0.105 + 14.103.10.1,5 — P=3,1.105N/m2(Pa)
17- R- C — veja teoria
18- Como o volume do cilindro que contém o gás se dilata muito pouco com a temperatura, pode-se dizer que se trata de uma transformação gasosa isométrica ou isovolumétrica (volume constante) — como o carro fica exposto ao sol, a temperatura do gás aumenta e consequentemente a pressão exercida pelo gás também aumenta, pois P/T=constante e P é diretamente proporcional a T — R- D
19- R- C — veja teoria
20- À temperatura constante (isotérmica), se a pressão diminui, no caso a externa, o volume aumenta, pois PV=constante — se a bola aumenta o volume, a pressão interna da bola diminui para igualar a pressão externa que também diminuiu — R- A
21- Pressão na profundidade de 20m=2atm (devido à coluna de água) + 1atm (pressão atmosférica na superfície da água) — P=3atm — isotérmica — P.V=K — Po.Vo=P.V — 1.Vo=3.V — V=Vo/3 — V=0,333Vo — R- A
22- Como a variação de volume dos pneus é desprezível, trata-se de uma isométrica, onde P/T=constante, sendo P diretamente proporcional a T — R- C
23- Até a explosão o volume do recipiente permanece constante (isométrica) — Pi/Ti=Pf/Tf — 2,0.105/78=4,0.105/Tf — Tf=156K — R- B
24- Isovolumétrica — Po/To=P/T — 2,3/(27 + 273)=2,53/T — 2,3T=759 — T=330K=330 – 273 — T=57oC
25- a) Se a porta do freezer fica aberta por algum tempo, parte do ar de seu interior é substituído pelo ar mais quente do exterior. Depois que você fecha a porta da geladeira, a temperatura interna do ar em seu interior irá diminuir e como se trata de uma isovolumétrica, a pressão também diminui (P/T=constante) fazendo com que a pressão externa fique maior que a interna, dificultando a abertura da porta. Mas, após alguns instantes, entra ar pelo sistema de vedação da geladeira, diminuindo a diferença entre as pressões externa e interna, facilitando, então, a abertura da porta.
b) Isovolumétrica — Point/To=Pint/T — 1,0.105/(27 + 273)=Pint/(-3 + 273) — Pint=0,9.105 N/m2 (Pa) — a diferença entre as pressões interna e externa sobre a porta da geladeira (ΔP) é igual à força resultante externa sobre a área da porta — ΔP=F/S —
(1,0.105 – 0,9.105)=F/(0,6×1) — 0,1.105=F/0,6 — F=6,0.103N
26-
27- Pressão à profundidade de 15m — P=Po + Págua a 15m=1,0 + 1,5 — P=2,5 atm — trata-se de uma isotérmica (temperatura permanece constante dentro da bolha) — Po.Vo=Pi.Vi — 1.Vo=2,5Vi — Vo=2,5Vi — R- D
28- a) Se a porta do freezer fica aberta por algum tempo, parte do ar de seu interior é substituído pelo ar mais quente do exterior. Depois que você fecha a porta da geladeira, a temperatura interna do ar em seu interior irá diminuir e como se trata de uma isovolumétrica, a pressão também diminui (P/T=constante) fazendo com que a pressão externa fique maior que a interna,
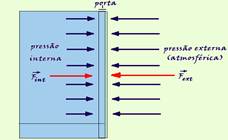
dificultando a abertura da porta. Mas, após alguns instantes, entra ar pelo sistema de vedação da geladeira, diminuindo a diferença entre as pressões externa e interna, facilitando, então, a abertura da porta.
b) Se a pressão externa é maior que a interna, como Pressão=Força/Área da porta, a força externa terá intensidade maior que a força interna e a intensidade da força resultante será FR=Fext – Fint — a transformação é isovolumétrica (volume constante) —
P1/T1=P2/T2 — 1,0.105x1.000=P2/(25 + 273) — P2=Pint=0,9.105N/m2 (Pa) — ΔP=FR/S — (1,0.105 – 0,9.105)=FR/2 — FR=0,2.105N — FR=2,0.104N
29- R- A — veja teoria
30- Isobárica — .V /T=constante — V é diretamente proporcional a T — R- B
31- Isovolumétrica — Po/To=P/T — 30/(27 + 273)=32/T — 30/300=T/32 — T=320K — T=320 – 273 — T=47oC —
R- D
32- Trata-se de uma transformação isobárica, pois a pressão exercida pelo ar no interior do cilindro é igual à pressão externa (atmosférica) exercida sobre a superfície livre da água — observe que o nível da água externa e internamente continuará sendo
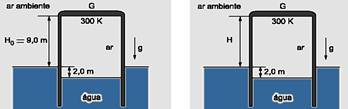
de 2m, pois o sistema está em equilíbrio e o empuxo é o mesmo (o peso do ar não varia) — volume inicial do ar — Vi=S.h=S.(2 + 9) — Vi=11.S (S é a área de seção transversal do cilindro) — volume final do ar — V=S.(H + 2) — isobárica — Vo/To=V/T — 11.S/300=(H + 2).S/360 — H=11,2m — R- D
33- Utilizando a equação de estado dos gases ideais, temos: p1V1 = n1RT1 e p2V2 = n2RT2e, portanto, 
. Como a parede é diatérmica e os gases estão em equilíbrio térmico, T1 = T2; como a parede pode mover-se sem atrito na horizontal e está em repouso, p1 = p2. Portanto, 
. Mas 
, logo, V2 = 2 V1. Substituindo esse resultado em V1 + V2 = Vo, obtemos 3V1 = Vo, ou seja, V1 = Vo/3 e, consequentemente,V2 = 2Vo/3.
34- Isotérmica — Po.Vo=P.V — 200.9=1.V — V=1.800 ℓ — 40ℓ – 1min — 1.800 ℓ – t min — t=1.800/40=45min —
R- C
35- Como não há trocas de calor com o meio externo, a temperatura continua sendo T — pressão final — Pi.Vi=Pf.Vf — P.(1/3)V=Pf.V — Pf=P/3 — R- B
36- antes de comprimir a bomba você tem n1 mol de ar no interior da bomba e n2 no interior do pneu — depois que o êmbolo desceu você terá no interior do pneu n mol tal que n=n1 + n2 — PV/RT=P1V1/RT1 + P2V2/RT2 — o processo é isotérmico — PV=P1V1 + P2V2 — P1=1 atm — P2=3atm — V1 (interior da bomba)=S.h=24cm2.30cm — V1=720cm3 — V1=0,72L — P.2,4=1.0,72 + 3.2,4 — P=3,3 atm — R- C
37- PoVo/To=P.V/T — T=To (do enunciado) — 1,6.105.3=P.4 — P=1,2.105 Nm2
38- P1V1/T1 + P2V2/T2= PfVf/Tf — P1V1 + P2V2= PfVf — P1V1 + P2V2= Pf(V1 + V2) — Pf=(P1 + P2)/2 — (5,0 + 18,0)/2 — Pf=11,5 atm — R- B
39-
40- a) Situação antes – cilindro fechado — situação depois – êmbolo já deslocado
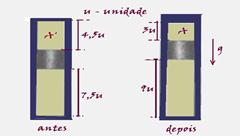
Antes — PA’=Patm=1,0.105N/m2 — VA’=4,5 unidades — TA’=27oC=300K
Depois — PA=? — VA=3 unidades — TA=27oC=300K
Isotérmica — PA’.VAPA.VA — 1.105.4,5=PA.3 — PA=1,5.105N/m2
b) Parte inferior do cilindro
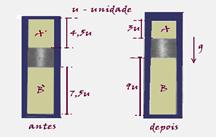
PB’.VB’/TB’=PB.VB/TB — 1.105.7,5/300=1,5.105.9/TB — TB=540K ou 267oC
41- a) P1 = F/S + Patmosférica = m.g/S + 105 = 160×10/0,16 + 105 = 10.000 + 105 = 104+ 105 = 0,1.105 + 105 — P1= 1,1.105 Pa
b) Pela lei geral dos gases — (p.V/T) = constante — (P1.V1/T1) = (P2.V2/T2) e como V = H.S pode-se ainda escrever — (P1.V1/T1) = (P2.V2/T2) — (P1.S.H1/T1) = (P2.S.H2/T2) — (P1.H1/T1) = (P2.H2/T2), mas o processo ocorre sob pressão constante e logo P1 = P2 então (H1/T1) = (H2/T2) — a partir dos dados disponíveis — (H1/T1) = (H2/T2) — (4/300) = (6/T2) — T2 = 1800/4 — T2 = 450 K
c) Para o cálculo da eficiência do processo R será necessário determinar a variação de energia potencial gravitacional da plataforma, DEP = m.g.DH e a quantidade de calor no processo Q que é dada por Q = m.c.DT — DEP = m.g.DH = 160.10.(6 – 4) = 3200 J — para o cálculo da quantidade de calor é necessário conhecer a massa de ar no cilindro. — como a densidade do ar a 300 K foi fornecida pode-se fazer — d = m/V — m = d.V = 1,1.0,16.4 — d= 0,704 kg — Q = m.c.DT = 0,704.103.(450 – 300) — Q=105.600 J — eficiência — R = 3.200/105.600 — R= 0,03 = 3%
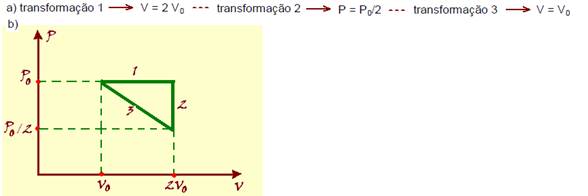
42- A lei geral dos gases afirma que P.V/T é constante — entre o estado A e B o volume é constante e logo P/T = constante —
(P/T)A = (P/T)B — P/300 = 2P/T — 1/300 = 2/T — T = 600 K — entre o estado B e C a temperatura é constante e logo P.V = constante — (P.V)B = (P.V)C — 2P.V = PC.(3V/2) — 4P/3 = PC — R- D
43- a) Falsa- é isovolumétrica — b) Correta- todos os pontos da curva AB tem a mesma temperatura — c) Falsa – o volume é constante — d) Falsa — mais afastada, T2>T1 — R- B
44- a) p.V/T = constante — 150.103.V/300 = 160.103.1,05.V/T — (1/2)= 160.1,05./T 
T = 168.2 = 336 K — T = 63°C
b) p.V/T = constante — 150.103.V/300 = p.1,08.V/360 — (103/2)= 1,08.p/360 — p = 167.103 Pa — p = 1,67.105 Pa
45- Isovolumétrica — Po/To=P/T — Po/(27 + 273)=P/(273 – 18) — P=(255/300)Po — P=0,85Po — P=85% da pressão inicial —
R- D
46- Isotérmica — Po.Vo=P.V — 1.105.100=P.140 — P=0,71.105 Pa — P=71.000Pa — R- C
47- R- C
48- Estado inicial — p = p0 — V = V0 — T = T0 — 1ª transformação — isotérmica — T1 = T0 e V1 = Vo/2 — P1V1/T1=PoVo/To — P1.(Vo/2)/To=PoVo/To — P1/2=Po — P1=2Po — 2ª transformação — Isobárica: p2 = p1 — V2 = 2 V0 — P1V1/T1=P2V2/T2 — (P1.2Vo)/To=(P1.Vo/2)/2To — 2/T2=1/2To — T2=4To — R- E
49-
50- Dados — D = 20 cm — R = 10 cm = 1 dm — p = 1 atm — T = 27 °C = 300 K — M = 30 g/mol — R = 0,08 atm·L/mol·K — π = 3 — volume da bola — V=(4πR3)/3=(4.3.13)/3 — V=4dm3 — V=4L — equação de Clapeyron —
pV=(m/M).R.T — m=(M.p.V)/RT=30.1.4/0,08.300=120/24 — m=5g — R- B
51-
Como o enunciado afirma que, durante o aquecimento não houve deformação da lata – Vi=Vf=V — dados: Pi=1atm — Ti=25oC=298K — Vi=V — Pf=? — Tf=621oC=894K — Vf=V — trata-se de uma transformação isovolumétrica (isocórica, isométrica) — Pi.V/Ti = Pf.V/Tf — 1.V/298 = Pf.V/894 — Pf=894/298 — Pf=3 atm — R- C