Resolução comentada dos exercícios de vestibulares sobre
dilatação linear, superficial e volumétrica dos sólidos e dilatação dos líquidos.
01- Como A está fixo, as dimensões do sistema devem aumentar, pois está sendo aquecido e o ponto B deve afastar-se de A (veja a figura)
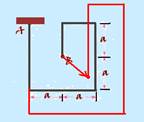
R- B
02- Quando a temperatura aumenta (θ > 27 ºC) o alumínio se dilata mais e ela se curva para cima e quando a temperatura diminui (θ < 27 ºC) o alumínio se dilata menos e ela se curva para baixo —
R- D
03- Sendo a barra de mesmo material (mesmo coeficiente de dilatação) e como sofre a mesma variação de temperatura, todos os seus pontos sofrerão a mesma dilatação e ela não será deformada — R- A
04- R- D — veja teoria
05- A dilatação do alumínio é o dobro da dilatação do aço — veja figura
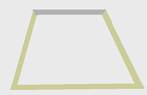
R- E
06- Observe que as lâminas estão se encurvando para dentro, então α2 > α1 e, quanto mais baixo estiver o contato (mais apertado o parafuso), menor será a dilatação das lâminas e consequentemente menor será a temperatura — R- D
07- R- B — veja teoria
08- Água fria contrai o interno e água quente dilata o externo — R- D
09- Sendo α1 (azul) maior que α2 (vermelho), com o aquecimento, a lâmina azul se dilata mais que a vermelha e a espiral se fecha (contrai) fazendo o ponteiro girar no sentido horário — R- E
10- Para que a ponte permaneça sempre na horizontal, os dois pilares devem sofrer a mesma dilatação para a mesma variação de temperatura — ΔL1= ΔL2 — L01.α1.Δt= L02.α2.Δt — 40.18.10-6=30.α2 — α2=24.10-6 oC-1.
11- ΔL=Lo.α.Δt=100.1,2.10-5.20 — ΔL=2,4.10-2m=2,4 cm — R- B
12- ΔL=Lo.α.Δt=12.1,1.10-5.40 = 528.10-5=52.800.10-5 — ΔL=0,528 cm — R- E
13- cálculo do coeficiente de dilatação da haste — ΔL=Lo.α.Δt — 2.10-2=103.α.1 — α=2.10-5oC-1 — ΔL=Lo.α.Δt=
800.2.10-5.20 === ΔL=32.000.10-5=0,32mm — R- B
14- ΔL = Lo . α . Δθ — ΔL = 30 . (11 . 10-6) . (40 – 10) = 99 . 10-4 m — R- C
15- ΔL=Lo.α.Δt — 15=1.000.α.(500 – 0) — R- α=30.10-6 oC-1
16- ΔL=Lo.α.Δt — ΔL=10.11.10-6(2,7 – 30) — ΔL=110.10-6.(-27,3) — ΔL= – 0,00303 — L=10,00 – 0,00303 — L=9,99697cm
17- aço de 0oC a 100oC — Laço=Lo(1 + α.Δt)=Lo + Lo.12.10-6.100) — Laço=1,0012Lo — vidro de 0oC a 100oC — Lvidro=Lo(1 + α.Δt)=Lo + Lo.8.10-6.100) — Laço=1,0008Lo — Laço – Lvidro=0,1 — 1,0012Lo – 1,0008Lo=0,1 — Lo=0,1/0.0004 = 0,25.103=250 cm — R- D
18- A reta A tem maior inclinação — R- C
19- Como o coeficiente de dilatação linear do latão é maior que o do aço, o latão se dilata mais quando aquecido e se contrai mais
quando resfriado — R- C
20- α=ΔL/LoΔt=0,24/2.200 —α=0,24/400 — α=0,0006 oC-1 — R- E
21- Para que o balanço permaneça sempre na horizontal, independente da temperatura, eles devem, para qualquer variação de temperatura, sofrer sempre a mesma dilatação ΔL — ΔLA=ΔLB — LA.1,5.10-5.Δt=72.2.10-5.Δt — LA=144.10-5/1,5.10-5 —
LA=96cm
22- Quanto maior o coeficiente de dilatação mais o corpo se dilata quando aquecido e mais se contrais quando resfriado.
(01) A se dilata mais que B — Correta
(02) Falsa — veja (01)
(04) A folga diminuirá — Falsa
(08) Possuem diferentes Lo — Falsa
(16) Apenas a placa se dilatará — Correta
(32) Apenas a placa se dilatará — Correta
R- (01 + 16 + 32)=49
23- R- A — veja teoria
24- Como um metal se dilata quando se aquece a estrutura metálica do lado direito do prédio passa a ter um comprimento maior do que a estrutura metálica em seu lado esquerdo devido ao aquecimento provocado pelo incêndio que ocorreu no lado direito. Para que a altura do prédio medida em seu lado direito fique maior do que a medida pelo lado esquerdo, o prédio entortará necessariamente para o lado esquerdo, como indicado na figura 2.
25- a) αA=ΔLA/LoAΔtA=0,0022/1,0022.100 — αA=22.10-6 oC-1 — αB=ΔLB/BΔtA=0,0011/1,0011.100 — αB=11.10-6oC-1
b) αA/αB=22.10-6/11.10-6 — αA/αB=2
26- Para que o circuito seja ligado com menor aumento de temperatura você deve escolher o que se dilata muito mais que o cobre, que no caso é o alumínio — R- B
27- a) Esfriou o conjunto, o alumínio tem maior coeficiente de dilatação e se contrai mais que o ferro.
b) ΔLAl=Lo.αAl.Δt — ΔLFe=Lo.αFe.Δt — ΔLAl/ ΔLFe=24.10-6/11.10-6≈2,2 — R- 2,2
28- Deve-se mergulhar a tampa do frasco na água quente. O zinco irá dilatar mais que o vidro, soltando-se do gargalo.
29- ΔV=0,006Vo — ΔV=Vo.γ.Δt — 0,006Vo=Vo.γ.200 — γ=3.10-5 oC-1 — α/1=γ/3 — α/1=3.10-5/3 — α=1,0.10-5 oC-1 —
R- A
30- a massa é a mesma para qualquer temperatura — d=m/V — volume inicial — 10=m/Vo — Vo=m/10 — volume final — 32oF=0oC — 10,03=m/V — V=m/10,03 —32oF=0oC — V=Vo.(1 + γ(t – to)) — m/10,03=(m/10).(1 + γ(0 – 100) — 1/10.03=1/10 – 100γ/10 — 1003γ=0,03 — γ=2,99.10-5=3.10-5 oC-1 — α/1=γ/3 —α/1=3.10-5/3 — α=1,0.10-5 oC-1 — R- B
31- a) Tempo que a chapa demora para atingir a elevação — ΔS=Vot + gt2/2 — 11.045=0.t + 10.t2/2 — t=√2.209 — t=47s — até abrir o pára-quedas ele demorou 5 minutos=5.60=300s — Δt=300 – 47=253s — Δt=253s
b) ΔS=So.β.Δt=500.4,8.10-5.(40 – -55) — ΔS=2,28cm2
32- O orifício se dilata na mesma proporção que a chapa, ou seja, de 4% — R- B
33- Δl=Lo.α.Δt=Lo.10-5.25 — ΔL=25.10-5Lo — R- D
34- Δd=0,02do — Δd=do.α.Δt — 0,02.do=do.α.100 — α=2.10-5 oC-1
espessura — ΔL=LoαΔt — ΔL/Lo=αΔt=2.10-5.100 — ΔL/Lo=2.10-3=0,2%
área — ΔS=So.β.Δt — ΔS/So=2αΔt=2.2.10-5.100 — ΔS/So=4.10-3=0,4%
volume — ΔV=Vo.γ.Δt — ΔV/Vo=γ.Δt =3.2.10-5.100 — ΔV/Vo=6.10-3=0,6%
R- D
35- a) ΔL=Lo.α.ΔT — α = ΔL/(Lo.ΔT) — metal I — αI=300.10-6/30 — αI=1,0.10-5oC-1 — metal II — αII=600.10-6/30 — αII=2,0.10-5 oC-1
b) A lâmina II deve estar na parte superior que deve se dilatar mais para que o dispositivo se encurve para baixo, pois ela tem maior coeficiente de dilatação.
36- R- C
37- ΔL=Lo.α.ΔT=2.22.10-6.110=484.10-5m — R=1 + 0,00484=1,00484m — S=πR2=3,1416.(1,00484)2 — S=3,172 m2
R-D
38- a) DL = a.L0.DT 
b) ΔV = g.V0.DT
c) ΔL = a.L0.DT
39- ΔV = Vo (γHg) DT — DV = Vo (3αHg) DT — ΔT=ΔV/3αHg.Vo=Ao.h/3αHgVo — ΔT=10-7.6.10-2/(3.40.
10-6.10-5)=6.10-9/120.10-11 — ΔT=5oC — ΔT=Tf – Ti — 5=Tf – 12 — Tf=17oC
40- a) O recipiente B porque se dilata menos.
b) O nível do líquido continuaria sendo o mesmo nos dois recipientes.
41- Sendo a densidade inversamente proporcionsal ao volume — R- D
42- R- A
43- Observe no gráfico que, se você diminuir a temperatura do sistema, o volume do recipiente fica menor que o da água e ela transborda e que se você aumentar a temperatura do sistema, o volume da água fica maior qie o do recipiente, e ela transborda — R- C
44- R- C — veja teoria
45- a) Correta — elas possuem a mesma densidade — estão em equilíbrio estático — o peso da esfera é igual ao empuxo.
b) Correta — sofrem dilatação volumétrica e a esfera se dilata mais que o óleo, deslocando mais líquido eaumentando o empuxo.
c) Correta
d) Falsa — a esfera se contrai mais que o óleo diesel, seu volume diminui mais e sua sensidade aumenta ficando maior que a do óleo diesel.
e) Correta
R- D
46- ΔLlíquido= ΔLaparente(tyransbordado) + ΔLfrasco — ΔLaparente(tyransbordado)= ΔLlíquido – ΔLrecipiente — R- B
47- 01. Falso — como a temperatura aumentou o volume do tanque também aumentou
02. Correto — a temperatura aumentou
04. Correta
08. Falsa — o tanque também se dilatou
16. Falsa — foi maior, pois parte da gasolina vazou
R- (02 + 04)=06
48- a) ΔVgas=Vo.γgas.Δt=15.000.9,6.10-4.(30 – 15) — ΔVgas=216 L
b) d=0,8g/cm3=0,8.103g/L — d=m/V — 0,8.103=m/20.000 — m=16.105g — Q=m.c.Δt=16.105.0,6.15 — Q= 1,44.108 cal
49- ∆V = γ .Vo.∆T — ∆V = 2.10-4.(S.20).4 — S.∆h = 160.S.10-4 — ∆h = 16.10-3m = 1,6 cm — ∆h=1,6cm
50- ∆Vtaça = γ .Vo.∆T=120.2,3.10-4.18=0,49cm3 — Val=120,49cm3 — ∆Vglic = γ .Vo.∆T=5,1.
10-4.119.18=1,092cm3 —
Vglic=120,092cm3 — a glicerina não transbordará pois a taça passará a ter um volume de 120,49 centímetros cúbicos, enquanto que o volume total da glicerina passará a ser de 120,092 centímetros cúbicos. Esta diferença 120,49 – 120,092 = 0,398 centímetros cúbicos é quanto ainda se poderia preencher de glicerina, na temperatura final.
51- ∆V = γ .Vo.∆T=4.104.1,1.10-3.20 — ΔV=880L — R- E
52- Analisando o gráfico, notamos que o volume específico diminui de 0 °C até 4°C, aumentando a partir dessa temperatura.
Aproximando os valores lidos no gráfico, constatamos uma redução de 1,00015 cm3/g para 1,00000 cm3/g de 0 °C a 4 °C, ou seja, de 0,00015 cm3/g. Isso representa uma redução percentual de 0,015%, o que é menos que 0,04 % — R- C
53- Quando o recipiente estiver completamente cheio de líquido, eles deverão ter o mesmo volume — ΔVV= ΔVL — 100(1 + 10-5(t – 10) = 99.(1 + 2.10-4)(t – 10) — t=19,6.10-2/18,6.10-3 — t≈10,5oC
54- O volume de glicerina que extravasou corresponde à dilatação aparente — ΔVap=Vo.γap.Δt — 352.10-3=10.γap.(90 – 10) —
γap=352.10-3/8.102 — γap=44.10-5 oC-1 — γg= γap+ γf — 5,0.10-4=44.10-5 + γf — γf=5,0.10-4 – 4,4.10-4 — γf=6,0.10-5 oC-1 —
αf=6.10-5/3 — αf=2,0.10-5 oC-1 — R- B
55- 
56-
b) T=2π√(L/g) — L=Lo.α.Δt — T=2π√( Lo.α.Δt/g)
57– ΔVap=Vo. γap.Δt — 25=500.γap.50 — γap=25/25.103 — γap=10-3 oC-1 — γlíq= γV = γap — γlíq=0,001 + 0,00001 —
γlíq=0,00101 oC-1
58- Cálculo de ℓ0A e de ℓ0B — ℓ0A. ℓ0B=75 — 3ℓ0B. ℓ0B=75 — ℓ0B=5cm e ℓ0A=15cm —
Após o aquecimento, os comprimentos finais das hastes são iguais, pois a figura transforma-se em um quadrado — ℓA= ℓB —
ℓ= ℓ0(1 + αΔt) — 15.(1 + αAΔt) = 5.(1 + αBΔt) — a relação entre os coeficientes de dilatação das hastes equivale a 9 e a variação da temperatura a 300 (320º – 20º) — logo — 15.(1 + 300.αB/9) = 5.(1 + 300αB) — 15 + 500αB=5 + 155αB —
αB= 1,0.10-2 oC-1
59- A expressão matemática que fornece o diâmetro do aro após aquecido ou resfriado vale — d = do(1+a.ΔT) — ao aquecer de 1ºC o aro da rede no lado do time visitante eles provocaram uma dilatação em seu diâmetro modificando-o para — d = 230,1(1+4,8.10-4.(21–20)) = 230,21mm — o que facilita a marcação de pontos pelo time local, já que o diâmetro do aro foi aumentado.
Por outro lado ao resfriar o aro da cesta em seu lado eles provocaram uma contração deste, reduzindo-o para — d = 230,1(1+4,8.10-4.(19 – 20)) = 229,99mm — assim, o time visitante não conseguirá marcar pontos, uma vez que o aro tem diâmetro menor do que o da bola.
As atitudes dos torcedores facilitaram as realizações de pontos para o time local e impossibilitaram a marcação de pontos pelo time adversário.
O técnico do time visitante está reclamando dessas atitudes dos anfitriões em utilizar conhecimentos científicos para fraudar o resultado da partida.
60- Observe que o valor do coeficiente de dilatação do alumínio é o dobro do coeficiente de dilatação do concreto e, como elas tem as mesmas dimensões iniciais e sofrem a mesma variação de temperatura, a chapa de alumínio se dilata dias vezes mais do que a de concreto — R- E
61- O fósforo acenderá primeiro no cubo que atingir a temperatura final de ignição mais rapidamente, ou seja, aquele que possuir maior condutividade térmica. Neste caso é o cubo feito de ouro, o cubo A. Quanto ao tamanho da aresta do cubo ela dilatará conforme seu coeficiente de dilatação, que é maior no chumbo. Assim a aresta do cubo A será menor que a do cubo B — R- A
62- O cobre deve se dilatar mais e deve ter maior coeficiente de dilatação — R- A
63- Dados: Ao = 1 m2 = 106 mm2; DA = 0,36 mm2 e Vo = 1 dm3 = 10-6 mm3 — DA = Ao.2 a DT — 0,36 = 10-6 2 a DT —
DT = 0,36/2.10-6=0,18/10-6 — DV = Vo3aDT — ΔV=10-6.3.0,18/10-6 — DV= 0,54 mm3 — R- B
64- Veja o esquema abaixo:
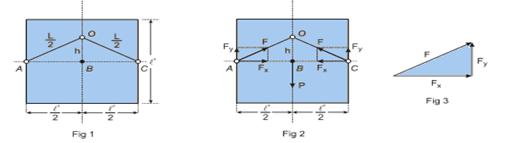
Nas figuras acima — ℓ: lado inicial do quadrado — ℓ’: lado do quadrado depois do aquecimento — L: comprimento da corda — h: distância OB — na Fig 1, no triângulo ABO, aplicando o teorema de Pitágoras — h2 + ℓ’2/4= ℓ2/4 — h2= ℓ2/4 – ℓ’2/4 — h=1/2.√ (ℓ2 – ℓ’2) (I) — na Fig 2, como o quadro está em equilíbrio, a resultante das forças é nula — assim — 2 Fy = P — 2 Fy = m g — FY=mg/2 (II) — o triângulo ABO da Fig 1 é semelhante ao triângulo das forças na Fig 3 — então — Fy/h=F/ ℓ/2 — substituindo nessa expressão as equações (I) e (II)
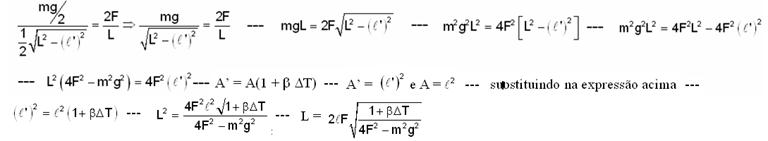
R- E
65- A expressão da dilatação superficial é: A = Ao (1+ b DT). Como As áreas finais terão que ser iguais — Aeixo = Aorif Þ 1,02 Ao [(1 + 5´10-5) (-50)] = Ao (1 + 5´10-5) DT — 1,02 – 2,55´10-3 = 1 + 5´10-5 DT — ΔT=0.02 – 2,55.10-3.5.10-6 — ΔT=349oC
66- Dados: R = 6.400 km = 6,4´106 m; L = 6,4 m; b = 
Da figura dada: sen q = 
O comprimento da base da área de avanço do oceano (DA) é b = 2 p r e a altura é L. Assim:
DA = (2 p r) L = (2 p R sen q) L. Mas:
DA = Aagua b DT. Igualando essas duas expressões:
(2 p R sen q) L = 
DT = 
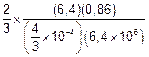DT = 
DT = 4,3 ´ 10–3 °C.
67- acat = A
a2 = 
68- ℓoA=0,99ℓoB — ℓA=ℓoA(1 + αA.∆t) — ℓA=0,99ℓoB(1 + αA.∆t) — ℓB=ℓoB(1 + αB.∆t) — quando o comprimento for o mesmo
— ℓA = ℓB — 0,99ℓoB(1 + αA.∆t) = ℓB=ℓoB(1 + αB.∆t) — 0,99ℓoB(1 + 10.10-5.∆t) = ℓB=ℓoB(1 + 9,1.10-5.∆t) — ∆t=1.250oC —
∆t=t – to — 1.250=t – 20 — t=1.270oC — R- C
69- Novo comprimento ℓ do pêndulo quando a temperatura subir de 10oC — ℓ = ℓo (1 + α(t – to) — ℓ = 10(1 + 10.10-6.10 —
ℓ=1,0001m — cálculo do período T que pelo enunciado vale T= √(4ℓ) — T= √(4.1,0001) — T= 2.√1,0001 s — para meio ciclo de oscilação o período será T=√1,0001 s — se, para cada meia oscilação o período aumenta de T=√1,0001 s, o relógio irá atrasar — R- C
70- Cálculo do coeficiente de dilatação linear do material — Lo=50m — L=50 + 50×0.02/100 — L=50,01m — ∆L= L – Lo=L0α∆θ — 0,01=50.α.20 — α=10-2/103 — α=10-5 oC-1 — o espaço (d) entre as barras é preenchido pelas duas metades das dilatações (∆L) de cada barra — d=2. ∆L/2=2.(0,01)/2 — d=0,01=10-2cm — ∆L=d=Loα∆θ — 10-2=50.10-5.∆θ —
∆θ=10-2/50×10-5=1.000/50 — ∆θ=20 oC
71- Todas estão corretas, com exceção da 08 que está errada pois, pela expressão ∆V=Vo.λ.∆θ você observa que o coeficiente de dilatação térmica (λ) é diretamente proporcional à dilatação (∆V) — R- (01 + 02 + 04 + 16) = 23
72– 01. Correta — embora esse “espaço vazio” deva, depois de algum tempo, ser preenchido com vapor d’água que se formará devido à baixa pressão.
02. Falsa — à temperatura de –5 °C, a água será congelada, aumentará de volume, estourando a garrafa.
04. Correta — essa dilatação observada é chamada de dilatação aparente — a dilatação real é soma da dilatação aparente com a dilatação da garrafa.
08. Falsa — tanto a água como a garrafa aumentam de volume.
R- (01 + 04) = 05
73- R- A.
74- Dilatometria – Estuda a dilatação dos corpos – Quando a temperatura de um sólido aumenta, surge um aumento da amplitude das vibrações atômicas e da distância média entre os átomos e moléculas que o constituem e então eles se
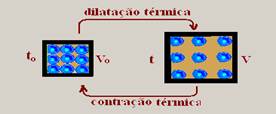
dilatam. Se a temperatura diminui, ocorre o fenômeno inverso, ou seja, eles se contraem.
16- Relação entre os coeficientes de dilação linear (α), superficial (β) e volumétrica (γ) — α/1 = β/2 = γ/3 — 1,5.10-3/1 =γ/3 — γ = 4,5.10-3 oC-1 — volume inicial da esfera — Vo=(4/3).π.R3=(4/3).3.(5)3 — Vo=500=5.102cm3 — ∆V=Vo. γ.∆θ=5.102.4,5.10-3.(110 – 10) — ∆V=225cm3 — R- E.
75- Quando a temperatura do trilho passar de 10oC para 40oC um comprimento de trilho de lo=25m sofrerá uma dilatação linear de — ∆L=Lo.α.(θ – θo)=25.14.10-6.(40 – 10)=10500.10-6 — ∆L=0,01m — o máximo comprimento do trilho a ser colocado deve ser — L=25,00 – 0,01=24,99m — R- D.
76- Depois que a régua foi resfriada ela se contraiu e o espaço entre cada unidade diminuiu fazendo com que a medida do mesmo lápis
aumente — R- A
77- Para qualquer tipo de dilatação no caso volumétrica, quanto maior o coeficiente de dilatação, maior será o volume dilatado, pois ∆V=Vo.γ.∆θ sendo γ o coeficiente de dilatação:
I. Falsa — a tampa deve se dilatar mais, ou seja, possuir maior coeficiente de dilatação.
II. Correta — ambos devem se dilatar mais para se desprenderem.
III. Correta — como a tampa possui maior coeficiente de dilatação ela se dilata mais pra aumento de temperatura ou se contrai mais para diminuição de temperatura.
IV. Correta — quanto maior a distância entre os átomos maior será a facilidade para se dilatar ou contrair com a variação de temperatura. — R- E