Calor latente – trocas de calor com mudança de estado – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Calor latente – trocas de calor com mudança de estado
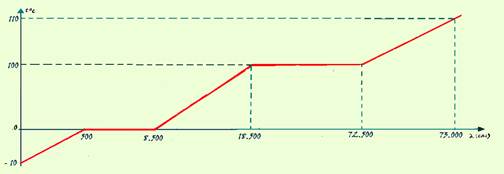
01- Aquecimento do gelo — Q1=m.c.(t – to)=100.0,5.(0 – (-10)) — Q1=500cal
Fusão do gelo — Q2=m.LF=100.80 — Q2=8.000cal
Aquecimento da água — Q3=m.c.(t – to)=100.1.(100 – 0) — Q3=10.000cal
Vaporização da água — Q4=m.LV=100.540 — Q4=54.000cal
Aquecimento do vapor — Q5=m.c.(t – to)=100.0,5.(110 – 100) — Q5=500cal
QT=Q1 + Q2 + Q3 + Q4 + Q5=73.000cal ou Q5=73kcal
02- a) Q=m.L — (200 – 100)=5.L — L=20cal/g
b) Q=m.c.(t – to) — (100 – 0)=5.c.(100 – 0) — c=0,2cal/goC
03- R- C — observe no gráfico
04- a) O primeiro trecho de gráfico corresponde ao aquecimento do gelo. Pela equação fundamental do calor sensível, Q = m.c.ΔT —
1000 = 100.c.20 — c = 0,5 cal/g.°C
b) O segundo trecho, uma linha horizontal sobre o eixo das abscissas, corresponde a fusão do gelo. Pela equação: Q = m.L —
8000 = 100.L — L = 80 cal/g
c) O terceiro e último trecho do diagrama corresponde ao aquecimento da água provinda da fusão do gelo. A capacidade térmica é dada pelo produto entre a massa e o calor específico sensível, ou seja, C = m.c — C = 100.1 = 100 cal/°C
05- Etotal = 1,6 ×1022 J (Energia total acumulada pela Terra) — Egelo = 3,2 ×105 J (Energia necessária para o derretimento de 1 kg gelo a 0°C) — regra de três — 1kg – 3,2.105J — mkg – 1,6.1022J — m=1,6.1022/3,2.105=0,5.1017J — m=50.1015kg — dividindo por 103 passa para tonelada — m=50.1012ton — m=50 trilhões de toneladas — R- B
06- Durante a fusão ele recebe Q=20cal/s.100s=2.000cal — Q=mL — 2.000=100.L — L=20cal/g — R- D
07- Aquecendo 2,5.103g de água de 18oC a 96oC — Q=mc(θ – θo)=2,5.103.1.(96 – 18) — Q1= 1,95.105cal — vaporização de 1,0.103g de água a96oC — Q=mL=103.540 — Q2=5,4.105cal — calor total — Qtotal=1,95.105 + 5,4.105 — Qtotal=7,35.105cal — Po=1.000W=1.000J/s — Po=1.000/4,2cal/s — Po=Q/Δt — 1.000/4,2=7,35.105/Δt — Δt=3.087s=51min
08- Pelo gráfico, em 24h 12kg de massa se fundem — portanto em 1h, se funde m=0,5kg — Q=m.L=0,5.320 — Q=160kj —
R- D
09- a) Substância B durante a fusão recebe de calor Q — Q=Po.Δt=20.(90 – 30) — Q= 1.200cal — Q=m.L — 1.200=50.L — L=24 cal/g
b) calor específico da substância B — Q=mcΔθ — Q=Po.Δt — Po Δt=mcΔθ — cB=Po. Δt/mΔθ=20.30/50.(80 – 20) — cA=0,2cal/goC — energia térmica (calor) liberada pela substância B quando sua temperatura diminui de 280oC a 80oC — QA=m.c.(80 – 280)=50.0,1.(-200) — QA= – 1.000 cal — energia térmica (calor) que a substância A deve receber para atingir a temperatura de 80oC — QB=m.c.(80 – 20)=50.0,2.60 — QB= 600cal — a fusão da substância B é realizada com Q=1000 – 600=400cal — Q=mL — 400=m.24 — mB=50/3g (parte de B que se liquefaz) — no estado sólido B fica com ms=50 – 50/3 — ms=100/3g — observe que a temperatura de equilíbrio térmico entre A e B é de 80oC.
10- Observe que, pelo gráfico TA>TB — como Q=m.L e como Q e m são as mesmas — LA>LB — R- C
11- a) fusão do gelo — Q=mgeloLf — potência da fonte — Po=Q/Δt — Q=Po.Δt — Po.Δt=mgelo.Lf — Po.60=mgelo.80 — 3Po=4mgelo (I) — aquecimento da massa (m=mágua + mgelo) de 0oC a 5oC — Q’=mc(θ – θo)=(2.400 + mgelo).1.(5 – 0) — Po.Δt’=(2.400 + mgelo).1.(5) — Po.20=12.000 + mgelo — 4Po=2.400 + mgelo (II) — dividindo membro a membro (I) e (II) —
3Po/4Po=4mgelo/2.400 + mgelo — mgelo≈553,85 g
b) Substituindo mgelo=554,85 em I — 3Po=4.553,85 — Po≈738,47cal/min
12- a) Q1 + Q2=0 — m1.c1.(T1-To1) + m2.c2.(T2-To2)=0 — 1000 × 1,0 × (T – 55) + 500 × 1 × (T – 25 ) = 0 — 1500 T = 67500 — T = 45 °C.
b) m=1.000 + 500=1.500kg — Q = 1500 × 1,0 × (100 – 45) = 1.500 × 55 = 82500 cal — Q=82,5 kcal.
c) Para resfriar a água — Q1 = – 1500 × 1 × 100 — Q1= – 150 000 cal — Para congelar a água — Q2 = – 80 × 1500 cal —
Q2=- 120 000 cal — portanto o calor total a ser RETIRADO da água será — Qt = Q1 + Q2 = – 270 000 cal — Qt= – 270 kcal.
13- a) Calor que a água (m=1kg=1.000g) perde quando fica em superfusão, se solidificando de 0oC a -5,6oC — Q=mcΔθ=1.000.1.(-5,6 – 0) — Q=-5.600cal — quando a superfusão cessa essa quantidade de calor torna sólida uma massa de água m com L=-80cal/g (perde calor ao se solidificar) — Q=mL — -5.600=m.(-80) — m=70g
b) Quando o bloco metálico de massa m=930g à temperatura θo=91oC é colocado no recipiente onde você tem gelo a 0oC, água a 0oC, todo o sistema é aquecido até à temperatura t — Fusão do gelo — Q1=mL=70.80 — Q1=5.600cal — aqucimento da água — Q2=mc(θ – θo)=1.000.1. (θ – 0) — Q2=1.000.θ — resfriamento do bloco metálico — Q3= mc(θ – θo)=C.(θ – θo)=400.(θ – 91) — Q3=400.θ – 36.400 — Q1 + Q2 + Q3=0 — 5.600 + 1.000.θ + 400.θ – 36.400=0 — 1.400.θ=30.800 —
θ=22oC
14- Potência da fonte térmica — Po=energia/tempo=Q/Δt=m.c.(θ – θo)/Δt=m.1.(100 – 10)/5 — Po=18m — intervalo de tempo para a vaporização da água — Q=Po.Δt=m.Lv — 18m.Δt=m.540 — Δt=15min — R- D
15- Calor necessário para fundir os 2 kg de gelo a 0 °C — Q = m.L = 2000.80 = 160000 cal — calor necessário para resfriar os 3 kg de água até 0 °C — Q = m.c.T = 3000.1.(0-40) = – 120000 cal — observe que o calor liberado pela água, 120 kcal, não é suficiente para fundir todo gelo (visto que são necessários 160 kcal) — portanto o equilíbrio térmico ocorrerá a 0 °C, sendo que os 3 kg de água líquida original continuará líquida e teremos uma parte do gelo derretida que vale — Q = m.L — 120000 = m.80 — m = 120000/80 = 1500 g = 1,5 kg — assim a quantidade de água gelada final será de 3 + 1,5 = 4,5 kg — R- D
16- A quantidade efetiva de energia utilizada foi — Q = m.c.∆T + m.L — Q = 1000.1.(100-20) + 500.540 — Q = 80000 + 270000 — Q = 350000 cal = 1.470.000 J — a quantidade de energia liberada foi — W = P.∆t — W = U.i.∆t — W = 127.12.(20.60) — W = 1.828.800 J — o rendimento (η) será — η =Q/W=1.470.000/1.828.800 — η=0,80 — η=80%
17- Volume que evaporou — V=1000mL – 950mL=50mL=50.10-6 m3 — V=0,050.10-3m3 — d=m/V — m=d.V — Q=m.L=d.V.L — Q=1,0.103.0,050.10-3.2,3.106 — Q=115.000J — R- B
18- a) P = U.i = 220.1 = 220 W = 220 J/s — Q = m.c.Δθ=1.4,2.103.(45 – 23)=1.4,2.103.22 — Q=9,24.104J — Po=Q/∆t — 220=9,24.104/∆t — ∆t=420s=7min
b) Se a água está a 45 °C e sua temperatura cai para 0 °C, há liberação de — Q = m.c. ∆θ = 1 . 4,2.103.45 = 189.000 J — para fundir todo o gelo são necessários Q = m.L = 0,6.330.000 = 198.000 J — como não ocorrerá o derretimento total do gelo, haverá gelo residual e, deste modo, a temperatura final desse experimento será 0 °C.
19- a)A sublimação do gelo seco ocorre devido ao calor absorvido pelo isopor — ms – massa de gelo seco que sofreu sublimação entre 18h e 24h — Δt=24 – 18=6h — Po=Q/Δt — Po=ms.L/Δt — 60=ms.648.103/6×3.600 — ms=2kg — se ele vai utilizar 2kg e 2kg foram sublimados, a massa total adquirida foi de mt=4kg
b) Número de mols de gelo secoque sofre sublimação — n=m/M=2.000/44 — n=45,4545 — n≈45,5 mol — nas condições normais de pressão e temperatura (CNTP), 1 mol do gás ocupariam 22,4L, então 45,5 mol ocuparão um volume de V=45,5.22,4 — V≈1.020L=1.020.103cm3 — V≈1,02.106cm3 — Como cada cm3 de gás formado carrega 0,01g, 1,02.106 cm3 carregará — mt=0,101.1,02.106=1,02.104g — mt=10,2kg
20- Devido ao alto calor específico da água, ela serve como regulador térmico para os seres vivos. Quando a temperatura do organismo aumenta, ele elimina água na forma de suor. Essa água, ao evaporar, absorve calor desse organismo, regulando sua temperatura. Cada 1 grama que se transforma em vapor absorve 540 cal — R- B
21- De água a 25oC a água a 120oC — Q1=m.c.Δθ=1.1.95 — Q1=95kcal — vaporizando a água a 25oC — Q2=m.L=1.526 — Q2=526kcal — Qtotal=95 + 526 — Qtotal=621kcal
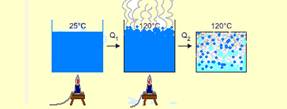
R- Qtotal=621 kcal.
22-
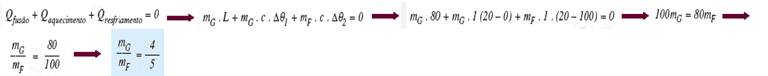
23-

24- Q(gelo) + Q(agua) + Q(água congelada) = 0 — 725.0,5.(0-x) + 2500.1.(0-5) + 64.(-80) = 0 — -362,5.x – 12500 – 5120 = 0 —
-362,5.x = 17620 — x = -17620/362,5 = -48,6°C
R- B
25- Quantidade de calor máxima cedida pela água ao gelo — Q=m.c.(t – to)=100.1.(0 – 30) — Q= – 3.000cal — essa quantidade de calor consegue fundir uma massa de — Q=m.L — 3.000=m.80 — m=37,5g — como existiam 100g de gelo e foram derretidos só 37,5g, sobraram no copo gelo e água a 0oC — R- C
26- Qcedidoágua + Qrecebgelo + Qrecfusãogelo + Qgelo+água=0 — mágua.cágua.(t – to) + mgelo.cgelo.(t – to) + mgelo.Lgelo + mgelo-água.cágua(t – to)=0 —
500.1.(30 – 40) + mgelo.0,5.(0 – (-7)) + 80mgelo + mgelo.1.(30 – 0)=0 — 113,5mgelo = 5.000 — mgelo=44g — R- B
27- a) Q= mágua.cágua.(t – to) + m.L=0,1×4.200x(0 – 20) + 0,1.3,3.105 — Q=80.570cal ou Q=80,57kcal
b) porta fechada — volume V constante — Lei geral dos gases perfeitos — Po.Vo/To=PV/T — 1/293=P/270 — P=0,92atm
28- a) Q=m.c.(t – to) + m.L=25.10-3.410.(30 – 10) + 25.10-3.80.000 — Q=205 + 2.000 — Q=2.205J
b)
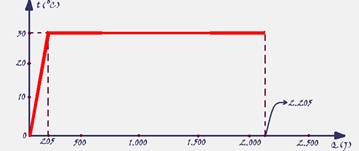
29- a) Po=Q/Δt — 750=Q/60 — Q=45.000J — 1g – 2.500J — m – 45.000J — m=45.000/2.500 — m=18g=0,018kg — a taxa é de 0,018kg/min
b) massa de água perdida pelo atleta — m=0,018kg/minx30min — m=0,54kg=0,54L
30– Q=m.L — Po=Q/Δt — Q=Po.Δt — mL= Po.Δt — m.2,26.103=113×3.600 — m=180g
31- msuco.csuco.(t – to) + mgelo.Lf + mágua.cágua.(t – to)=0 — 250.1.(t – 20) + 50.80 + 50.1.(t – 0)=0 — 250t – 5.000 +4.000 + 50t=0 — t=3,3oC
32- mchumbo.Lf + mchumbo.cchumbo.(t – to) + mágua.Lv=0 — -300.5,5 + 300×0,03(100 – 327) + m.540=0 — m=6,8g — R- E
33– Observe que a temperatura inicial e final do óleo é a mesma, então ele pode ser excluido da resolução do exercício — fusão do gelo a 0oC — Q1=mL=40.80 — Q1=3.200cal — água de 00C a 30oC — Q2=mcΔθ=40.1.30 — Q2=1.200cal — massa m de água a 70oC sendo resfriada até a temperatura θ — Q3=mc(θ – θo)=m.1.(30 – 70) — Q3=-40m — Q1 + Q2 + Q3=0 — 3.200 + 1.200 – 40m=0 — m=110g
34- Em 1 s é fornecida a quantidade de calor — Po=800W=800J/s =Q/Δt — Q=800J=800/4,2cal — esse Q aquece água de 20oC a 100oC (Q1) e depois a vaporiza a 100oC (Q2) — Q1= mc(θ – θo)=m.1.80=80m — Q2=mL=m.540 — Q=Q1 + Q2 — 800/4,2=540m + 80m — m=0,31g — d=m/V — 1g/mℓ=0,31g/V — V= 0,31mℓ — vazão — Va=0,31/1 — Va=0,31 mℓ/s
35- De acordo com o gráfico no instante inicial a temperatura da água é de 10 °C e no instante 50 s é de 30 °C — a quantidade de calor absorvida pela água foi de Q = m.c.DT = 200.1.(30-10) = 4000 cal — o que significa que a fonte de calor possui fluxo de 4000 cal/50 s = 80 cal/s — a partir do instante inicial considerando-se 135 s o total de calor fornecido para água, por esta fonte, será de 135.80 = 10.800 cal — Q = m.c.DT — 10.800 = 200.1.(T – 10) — T = 64°C — Para fundir 200 g de gelo são necessários — Q = m.L = 200.80 = 16000 cal — com um fluxo de 80 cal/s — 16000/80 = 200 s — R- A
36- a)Observe nos gráficos que a mudança de estado físico, solidificação, ocorreu entre as leituras de calor 16.104 J (veja no gráfico maior) e 1.104 J (veja no detalhe gráfico a direita) — Q = m.L — (1.104 – 16.104) = 0,5.L — -15.104 = 0,5.L — L = -30.104 =L=-3,0.105 J/kg
b) o resfriamento na fase sólida pode ser lido no detalhe gráfico, onde se pode ver que este resfriamento ocorreu entre 1.104 J e zero. — Q = m.c.DT — (0 – 1.104) = 0,5.c.(-10 – 0) — -104 = -5.c — c = 2000 J/(kg°C) = 2 kJ/(kg°C)
37- Calor de fusão do gelo — Qg = mLg = m(80) — calor sensível da água: Qa = mcaDT = m(1)(100) = m(100) — calor de vaporização da água: Qv = mLv = m(540) — a quantidade de calor até o instante t é — Q = Qg + Qa + Qv = m(80) + m(100) + m(540) = m(720) — como o calor é fornecido à taxa constante, até o instante t/2 a quantidade fornecida é Q/2= m(360) — essa quantidade de calor é suficiente para derreter o gelo e aquecer a água até 100°C e vaporizar uma massa m’ de água, que pode ser calculada por — m(360) =m(80) + m(100) + m’(540) — m’(540) = m(360) – m(180) — m’(540) = 180 m Þ m’ =m/3 — assim, na metade do tempo teremos uma mistura de água e vapor a 100 °C, restando 2/3 da massa inicial da água — R- C
38- a) Dado: m = 100 g. — pela leitura do gráfico, conclui-se que — de 0°C até 40 °C a substância esteve na fase sólida — a fusão ocorreu na temperatura de 40 °C com absorção de 400 cal — após a fusão, iniciou-se novo aquecimento, de 40 °C a 80 °C — na fase líquida a quantidade de calor absorvida foi — Qs = 1.000 – 600 = 400 cal — Qs = m c DT — c=Q/mΔT —
Q=400/100×40 — c = 0,1 cal/g.°C — durante a fusão, a temperatura se manteve constante, absorvendo nesse processo — Q = 600 – 200 = 400 cal — QL=mL — L=400/100 — L=4 cal/g
b) Dados: mg = 50 g; Lg = 80 cal/g; cag = 1 cal/g.°C — quantidade calor necessária para fundir totalmente o gelo — Qg = m Lg — Qg = 50 (80) = 4.000 cal — se a substância recebeu 1.000 cal para aquecer de 0 °C até 80 °C, para retornar a 0°C, fazendo o processo inverso, ela liberou, também, 1.000 cal, que foram absorvidas pelo gelo — essa quantidade é insuficiente para fundir totalmente o gelo — a massa (m’) de gelo fundida é, então, a que recebeu Q’= 1.000 cal — Q’= m’ Lg Þ 1.000 = m’ (80) —
m’ = 12,5 g.
39-

40- m = 100 g; cgelo = 0,5 cal/g.°C; Lfusão = 80 cal/g; cágua = 1 cal/g.°C; LV = 540 cal/g; Dt = 5 min = 300 s e 1 cal = 4,2 J — a quantidade de calor total é igual ao calor sensível do gelo de –10°C até 0 °C, mais o calor latente de fusão do gelo, mais o calor sensível da água de 0 °C a 100 °C e mais o calor de vaporização da água — Q = Qgelo + Qfusão + Qágua + Qvaporização — Q = m cgelo DTgelo + m Lfusão + m cágua DTágua + m LV — Q = 100 (0,5) [0 – (-10)] + 100 (80) + 100 (1) (100 – 0) + 100 (540) —
Q = 500 + 8.000 + 10.000 + 54.000 — Q= 72.500 cal=72.500×4,2 — Q=304.500J — Po=Q/Δt=304.500/300 — Po=1.015W — R- C
41- mágua = 200 g; mgelo = 150 g; to = 30 °C; cágua = 1 cal/g.°C; Lgelo = 80 cal/g — nesse tipo de problema, envolvendo gelo e água, você precisa sempre verificar se, no equilíbrio térmico, sobra gelo ou se há fusão total — para isso, tem que comparar o calor latente necessário para fusão do gelo (Qgelo) com o calor sensível liberado pela água (Qágua) até 0 °C —
Qgelo = mgelo Lgelo = 150 (80) — Qgelo = 12.000 cal — Qágua = mágua cágua DT = 200 (1) (0 – 30) — Qágua = – 6.000 cal ( o sinal negativo indica apenas que houve liberação de calor) — Comparando essas quantidades de calor (em módulo), verificamos que a quantidade de calor necessária para fundir o gelo (12.000 cal) é menor que a quantidade de calor liberada pela água (6.000 cal — apenas metade da necessária). Portanto, apenas metade da massa de gelo se funde e a temperatura de equilíbrio térmico é 0 °C.
R- C
42- Quantidade calor liberada pela água para o resfriamento desejado — Qágua = m água cágua |DT| = 200 (1) |20 – 24| — Q=-800cal
— quantidade de calor necessária para fundir um cubo de gelo — Qcubo = mcubo Lfusão = 10 (80) = 800 cal — Qágua + Qcubo=0
— sendo a quantidaded de calor cedida igual à recebida, você deve observar que basta um cubo de gelo para provocar o resfriamento desejado da água — R- A
43- Fusão do gelo Q1=mL=50.80 — Q1=4.000cal — resfriando água de 80oC a 0oC — Q2=mcΔt=150.1.80 — Q2=- 12.000cal —
o calor fornecido pela água derreteu o gelo e ainda sobraram 8.000cal para aquecer as (150 + 50)g restantes até uma temperatura t — Q=mcΔt — 8.000=200.1.(t – 0) — t=8.000/200 — t=40oC — R- E
44- A quantidade de calor liberada pelo fogão é — Q = P Dt = m L Þ m = P.Δt/L=300×600/2,25.103 — m=80g — R- C
45- água a 30oC a água a 100oC — Q1=mcΔθ=0,5×4.190.(100 – 30) — Q1= 146.650J=146.65kJ — vaporizando água a 100oC — Q2=m.L=0,5.2.246 — Q2=1.123kJ — Q=Q1 + Q2=146,65 + 1.123=1.269,65kJ — R- B
46- Quantidade de calor que deve ser retirada do corpo para que sua temperatura diminua de 37oC para 30oC — Q=mcΔθ=60.1.(30 – 37) — Q= – 420kcal — essa quantidade de calor em módulo deve ser fornecido pelo gelo a 0oC e fusão — Q=mL — 420=m.80 — m=5,25kg — R- E
47- No sentido científico, supondo que a água esteja fervendo a céu aberto, ao nível do mar, haverá, por conta do recebimento de
energia (calor), ebulição — a temperatura da massa líquida permanecerá constante e sempre de 100oC, logo, a energia cinética

média por molécula permanecerá constante — porém, haverá cada vez menos moléculas na massa líquida — portanto, a quantidade de energia da massa líquida diminui, apesar do recebimento de energia — assim, se você entendesse a quantidade de calor do corpo como temperatura, como na linguagem corrente, sería obrigado a dizer que a temperatura da água diminui durante o tempo em que estiver fervendo — R- A
48- Dados — L = 2,2.103 J/g — P = 300 W — ∆t = 10 min = 600 s — quantidade de calor liberada pelo fogão — P=Q/∆t —Q=P.∆t — Q=m.L —P. ∆t=m.L — m=P.∆t/L=300.600/2,25.103 — m=80g — R- C
49- 01. Correta — veja teoria
02) Correta — veja como exemplo a fusão da água — na patinação sobre o gelo, o deslizamento é facilitado porque, quando o

patinador passa, parte do gelo se transforma em água, reduzindo o atrito — estando o gelo a uma temperatura inferior a 0ºC, isso ocorre porque a pressão da lâmina do patim sobre o gelo faz com que ele derreta — isso ocorre porque um aumento da pressão diminui a temperatura de fusão — outro exemplo, vaporização da água — uma panela de pressão cozinha alimentos em água em um tempo menor do que as panelas comuns — esse desempenho da panela de
pressão se deve ao fato de que a tampa provoca no interior da panela um aumento da pressão que, por sua vez provoca também um aumento na temperatura de vaporização fazendo a água ferver a uma temperatura acima de 100oC.
04. Correta — veja teoria
08. Correta — com o aumento de temperatura, a energia cinética média das moléculas aumenta, e assim, mais moléculas conseguem se transformar em vapor, aumentando a velocidade de evaporação.
R- (01 + 02 + 04 + 08) = 15
50- Dados — V = 2 L — P = 420 W — c = 1 cal/g.°C = 4,2 J/g.°C — L = 540 cal/g = 2.268 J/g — d = 1 kg/L — ∆T = (100 – 20) = 80 °C — massa de água usada — d=m/V — 1=m/2 — m=2kg=2.000g — quantidade de calor necessária para que 20% da massa (0,2 M) de água seja vaporizada — Q = Qsensível + Qlatente — Q = M c ∆T + (0,2 M) L — Q = 2.000 (4,2) (80) + (0,2×2.000)x2.268 = 67.200 + 907.200 — Q = 1.579.200 J — a potência útil é 20% da potência total — Pútil = 0,8 P = 0,8 (420) — Pútil = 336 W — Pútil=Q/∆t — ∆t=Q/Pútil=1.579.200/336 — ∆t=4.700s — ∆t=1h, 18min e 20s — R- B
51- a) Cálculo da área da tampa (40 cm:50 cm) — A = 0,4 m.0,5 m — A=0,2m2 — potência solar incidente na Terra (placa e
consequentemente na água) (1 kW por m2) — 1m2 – 1 kW — 0,2m2 – Po — Po=0,2.1 — Po=0,2 kW
b) A quantidade de energia (E) necessária para aquecer a água no interior da panela é dada por — Q=E=mc∆t — E=300.4.(100 – 25) — E=90.000J ou E=90 kJ
c) A quantidade de energia (E‘) para aquecer a água de 25oC até 100°C é de 90.000 J (item anterior) — para evaporar 1/3 da água — m=300/3=100g — Q’=E’=mL=100.2.200 — E’ = 220.000 J — Etotal = =90.000 + 220.000 — Etotal=310.000 J —
Po=Etotal/∆t — 200=310.000/∆t — ∆t=1.550 s
52-
V=300ml=300.10-3l=0,3l=0,3.103cm3 — d=mV — 1=m/0,3.103 — m=0,3.103g=300g — como a água não evapora, trata-se apenas de calor sensível, sem mudança de estado — Q=m.c.(θ – θo)=300.1.(40 – 10) — Q=9.000 cal — R- D
53- Como o enunciado pede para considerar o sistema água e gelo isolado haverá trocas de calor somente entre eles e, ao final dessas trocas você terá apenas água líquida à temperatura de equilíbrio térmico θe — Q – quantidade de calor cedido pelos 200g de água a 25oC para sua temperatura passar de 25oC a θe — Q=m.c.(θe – θ)=200.1.(θe – 25) — Q=200.θe – 5000 — Q’ – calor recebido pelos 50g de gelo a 0opara mudar de estado e se transformar em 50g de água a 0oC — Q’=m.L=50.80 — Q’=4000cal
Q’’ – calor absorvido pelos 50g de água a 0oC a 50g de água a θe — Q’’=m.c.(θe – 0)=50.1.θe — Q’’=50.θe — a soma algébrica dessas quantidades de calor trocadas pelo sistema é nula — Q + Q’ + Q’’ = 0 — 200.θe – 5000 + 4000 + 50.θe=0 —
250.θe = 1000 — θe=4oC
02- Maior — você pode, agora incluindo o copo nas trocas de calor, efetuar o equilíbrio térmico entre toda a água (250g) a 4oC com o copo que está a 25oC e, é claro que a temperatura final estará entre 4oC e 25oC, ou seja, será maior que 4oC.
54- Como a fusão e a vaporização ocorrem à temperatura constante, pelo gráfico a fusão ocorre à temperatura de 40oC e a
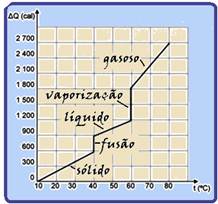
vaporização à temperatura de 60oC — portanto entre 10oC e 40oC o corpo se encontra no estado sólido, entre 40oC e 60oC, no estado líquido e, a partir de 60oC no estado gasoso — calor específico no estado sólido — Q=m.c.(θ – θo) — (600 – 0)=50.c.(40 – 10) — c=0,4cal/goC —
A vaporização ocorre na temperatura de 60oC e para isso o corpo recebeu Q=1.800 – 1.200=600cal — Q=m.L — 600=50L — L=12cal/g — R- B
55- De gelo a -20oC a gelo a 0oC — calor sensível — Q1=m.cgelo.∆θ=2.0,5.[0 – (-20)] — Q1=20kcal — de gelo a 0oC a água a 0oC — calor latente de fusão — Q2=m.L=2.80 — Q2=160kcal — de água a 0oC a água a 50oC — calor sensível — Q3= m.cágua.∆θ=2.1.(50 – 0) — Q3=100kcal — Qtotal=20 + 160 + 100=280kcal — como a fonte térmica fornece 20kcal por minuto — t=280kcal/20kcal/min=14minx60=840s — R- D.
