Átomo de Bohr – Estrutura Atômica

Resolução comentada dos exercícios de física sobre

Estrutura Atômica – Átomo de Bohr

 

01- Quando o elétron salta novamente para sua órbita original, de níveis de energia mais baixos, o que faz com que a energia seja liberada através da emissão de um fóton luminoso.  —  R- B

02- R- D  —  veja teoria

03- I. Falsa  —  não é contínua, só pode ter valores determinados.

II. Correta.

III. Correta.

R- D

04- ΔE=h.f=h.c/λ  —  3,4.10-19=6,6.10-34.3.108/λ  —  λ=5.824.10-10 m  —  R- B

05- Observe que para saltar do nível 1 (n1) para o nível zero (n∞), onde o elétron se ioniza, foram gastos (E1 – E∞)=│-13,6 – 0│= 13,6 eV  —  como recebeu 20 eV e gastou 16,3 eV, vão sobrar  —  20,0 – 13,6=6,4 eV  — R- C

06- R- C  —  veja teoria

07- Lembre-se de que a velocidade de todas as cores e de todas as radiações eletromagnéticas é sempre a mesma no vácuo e, aproximadamente no ar (3,0.108m/s)  —   cada cor tem velocidades diferentes em outros meios homogêneos e transparentes (vidro, água, etc.) —  a energia de cada cor é diretamente proporcional à freqüência (f) e inversamente proporcional ao comprimento de onda (λ)  —  da tabela, o menor λ, a mais energética é a violeta  —  R- C

08- Na transição de 2 para 1  —  ΔE=(-3,4) – (-13,6)  —    ΔE=10,2 eV  —  compatível com f2, que será absorvido  —  De 3 para 1  —    ΔE=(-1,5) – (-13,6)  —    ΔE=12,1 eV  —  compatível com f1, que será absorvido  —  de 3 para 2  —    ΔE=(-1,5) – (3,4)  —  ΔE=1,9 eV  —  incompatível com f3, que não será absorvido  —  R- f1 e f2.

09- Quando a transição ocorrer de um nível mais alto de energia para um nível mais baixo (órbita mais externa para órbita mais interna), ocorre a emissão de um fóton  —  como ao menor comprimento de onda corresponde a maior freqüência e consequentemente maior nível energético você deve escolher a alternativa em que ocorre maior variação de energia  —  R- C

10-  │ΔE│x= hc/λ=4,13.10-15.3.108/1,03.10-7  —  │ΔE│x=12.03 eV  —  │ΔE│y= hc/λ= 4,13.10-15.3.108/4,85.10-7  —  │ΔE│y=

2,55 eV  —  os valores mais próximos são de 2 e 6  —  │ΔE│2= 13,6 – 1,51=12,09  —  │ΔE│6=3,40 – 0,85=2,55  —  R- B

11- ΔE=E2 – E1=(-3,4) – (-13,6)  —  ΔE=10,2 eV=10,2.1,6.10-19  — ΔE= 16,3.10-19J  —  ΔE=h.f  —  f=16,3.10-19/6,63.10-34  —  f=2,5.1015Hz

12- a) Pelo gráfico, a intensidade é máxima quando f=1,8.1013 Hz  —  c=λf  —  3.108=λ.1,8.1013  —  λ=1,7.10-5m

b) Estimando a área, considere a pessoa como um cilindro de 0,3m de diâmetro e altura 1,7m  —  A=2πRh + 2πR2=2.3.0,15.1,7 + 2.3.(0,15)2  —  A≈1,7m2  —  Po=E/Δt  —  σA(T4 – T4a) = E/9.104  —  6.10-8.1,7.((37 + 273)4  – (27 + 273)4)=E/9.104  — 

10,2.10-8.(3104 – 3004)=E/9.104  —  E=10,2.10-8.9.104.(9.235.210.000 – 8.100.000.000)  —  E≈1,04.107 J

13- Se os fótons foram emitidos, o elétron pulou da órbita 2 para a 1  —  E2 – E1= -3,40 – ( -13,6)  —  ΔE= + 10,2 eV  —  R- D

14- O exercício está afirmando que a freqüência do vermelho é menor que a do verde  —  a freqüência é diretamente proporcional ao nível energético  —  Evermelho < Everde  —  a freqüência é inversamente proporcional ao comprimento de onda λ e consequentemente ao nível energético E  —  λvermelho > λverde  —  R- B

15- Para o átomo de hidrogênio  —  (E4 – E1)=- 13,6(1/(n4)2 – (n1)2)  —  ΔE= – 13,6.(1/16 – 1/1)  —  ΔE= – 13,6.(-15/16)  — 

ΔE= +12,75 eV  —  ou  —  ΔE=12,75.1,6.10-19=20,4.10-19J  —  ΔE=h.f  —  20,4.10-19=6,63.10-34.f  —  f=3,07.1015 Hz

16- Nas radiografias os  ossos saem brancos e tecidos em volta negros  —  isso ocorre porque o osso, cuja estrutura é mais densa que a do tecido mole, absorve mais radiação ficando com aparência clara enquanto que o tecido mole, menos denso, é atravessado pelos raios X, ficando com aparência mais escura  —  R- C

17- Lembre-se de que a energia dos fótons de luz é diretamente proporcional à frequência da luz f  —   como a freqüência da luz amarela, do sódio, é menor, então sua energia também é menor  —  a velocidade de propagação de todas as cores e de todas as radiações eletromagnéticas é sempre a mesma no ar e no vácuo (c=3,0.108m/s)  —  R- A

18- Basta substituir na equação, que é fornecida, lembrando que a velocidade v é c (velocidade da luz)  —  V2=2GM/R  —  R=2GM/c2   —  R=2.6,67.10-11.5,98.1024(3.108)2  —  R≈9.10-3m  —  diâmetro d=2R=2.9.10-3=18.10-3=0,018m=1,8cm

19- Fissão Nuclear  —  reação que se inicia com o choque de um nêutron com um núcleo instável que proporciona a quebra deste último e, por este motivo, é chamado de fissão nuclear (divisão do núcleo)  —  Fusão Nuclear – é o processo no qual dois ou mais núcleos atômicos se juntam e formam um outro núcleo de maior número atômico.

O principal tipo de fusão que ocorre no interior das estrelas é o de Hidrogênio em Hélio, onde dois prótons se fundem em uma partícula alfa (um núcleo de hélio), liberando dois pósitrons, dois neutrinos e energia.

20- 

R- B

21- R- D  —  veja teoria

22- E1=Eo  —  n=1  —  E1=-Eo/12  —  E1=-Eo  —  n=4  —  E4=-Eo/42  —  E4=Eo/16  —  E1 – E4=(-Eo) – (-Eo/16)  —  ΔE1,4=(-15/16).Eo  —  R- D

23- Observe no gráfico 1 a queda de intensidade de radiação quando os raios X atravessam a parte maciça do cilindro em teste  —  no gráfico 2 você observa que a metade esquerda do cilindro, em comparação com o gráfico 1, deve ser maciça e a metade direita oca  —  R- E

24- R- A  —  veja teoria

25- A força nuclear forte é a responsável pela atração mútua entre os nêutrons e prótons do núcleo atômico  —  a força nuclear fraca participa das transmutações atômicas  —  a força elétrica está associada aos campos elétricos criados em torno das cargas elétricas

  —  a força gravitacional é uma das mais presentes em nosso cotidiano, haja vista que nosso peso é uma manifestação gravitacional  —  R- C

26- Velocidade da luz no vácuo  —   c = 3.108 m/s  —   constante de Planck  —   h = 6,6.10-34 J·s = 4,1.10-15 eV·s   —   combinando a equação fundamental da ondulatória com a equação de Planck  —  E=h.c/λ  —  para a linha Hα  —  λ=656,3.10-9  —  E=4,1.10-15.

3.108/653,6.10-9  —  E≈1,88 eV  —  R- D

27- De acordo com o postulado de Bohr, o elétron excitado passa para um nível mais energético  —  Ao sofrer decaimento para o nível estacionário, ele emite um fóton, que dependendo da frequência, poderá ser ou não na forma de luz visível  —  R- A   

 

28- (I) Incorreta  —   intensidade de radiação emitida aumenta com a temperatura  —   I=σ.T4  —  portanto, T3 > T1.

(II) Correta  —  pelo gráfico

(III) Incorreta  —  pelo gráfico, vemos que o comprimento de onda para o qual a radiação é máxima é menor para T3.

(IV) Incorreta. Já justificado em (I).

(V) Incorreta. Já justificado em (I).  

R- E 

29- A lei de Stefan-Boltzmann afirma que a potência total irradiada pelo corpo negro é diretamente proporcional à área (S) da superfície emissora e diretamente proporcional à quarta potência da temperatura absoluta (T): P = sST4  —  a equação do efeito fotoelétrico dada por Einstein afirma que quando uma onda eletromagnética de alta frequência atinge uma chapa metálica, cada fóton pode arrancar um único elétron que é ejetado com energia cinética máxima (K) dada pela expressão  —  K = h f – W, sendo h a constante de Planck, f a frequência da onda incidente e W o trabalho para arrancar o elétron do metal  —  a equação de Louis de Broglie concilia as características ondulatórias e corpusculares dos fenômenos relacionados à luz, através da equação  —  λ=h/Q, sendo l o comprimento de onda associado ao movimento da partícula que se desloca com quantidade de movimento (momento linear) Q  —  R- C

30- a) Os fótons incidentes que podem ser absorvidos são determinados a partir das diferenças de energia entre os estados inicial (nível fundamental) e final (1º, 2º ou 3º nível)  —  aqueles fótons cujas energias coincidem com uma das diferenças de energia entre os níveis mostrados na figura poderão ser absorvidos  —  as diferenças de energia entre os estados inicial e final são dadas por  —  DEf3 = – 0,85 – ( -13,60) = 12,75eV (nível fundamental e 3o nível)  —  DEf2 = – 1,51 – ( -13,60) = 12,09eV (nível fundamental e 2onível)  —  DEf1 = – 3,40 – ( -13,60) = 10,20eV (nível fundamental e 1o nível)  —  logo, os fótons que podem ser absorvidos pelo átomo de hidrogênio no estado fundamental são aqueles cujas energias são respectivamente iguais a: 12,09 eV, quando o átomo é excitado do estado fundamental para o 2º nível, e 10,20 eV, quando o átomo é excitado do estado fundamental para o 1º nível.

b)

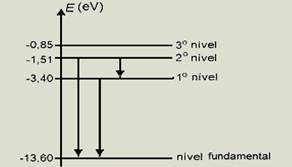
c) As energias dos fótons emitidos são determinadas a partir da diferença de energia entre o nível inicial e o nível final  —  portanto, os fótons emitidos terão as seguintes energias  —  DE2f = -1,51 – ( -13,60) = 12,09eV  —  DE1f = -3,40 – ( -13,60) = 10,20eV  —  DE21 = -1,51 – ( – 3,40) = 1,89eV

31- 1. Tomando os níveis 0, 1 e 2 de energias Eo, E1 e E2, tal que Eo < E1 < E2 (ver representação na figura acima) para transições do nível 2 para o 0, temos duas hipótese  —  1ª hipótese  —   emissão de 1 fóton de energia E = h . f – E2 – Eo  —  2ª hipótese  —   emissão de 2 fótons de energias E’ = h . f’ = E2 – E1 e E” = h . f” = E1 – Eo  —  por conservação da energia  —   (E2 – Eo) = (E2 – E1) + E1 – Eo)  —  E = E’ + E’ e assim, h . f = h . f’ + h . f”  —  f = f’ + f”  —  portanto, cada frequência pode ser a soma ou a diferença entre outras.

2. Os comprimentos de onda que limitam a região do visível são l = 4,0.10-7 m e l’ = 7,0.10-7m (tabela de constantes), que correspondem, respectivamente, às frequências f=3.108/4.10-7  — f=7,5.1014 Hz  —  f’=3.108/7.10-7  —  f’=4,3.1014 Hz

32- R- A  —  veja teoria

33- R- B  —  veja teoria

34- a) E=h.c/ λ  —  1,98.10-15=6,6.10-34.3.108/λ  —  λ=19,8.10-26/1,98.10-15  —  λ=10-10m  —  λ=1 A

b) Q – quantidade de movimento  —   λ=h/mv  —  λ=h/Q  —  Q=h/λ=6,6.10-34/10-10  — Q=6,6.10-24 kg.m/s

35- R- D

36-

R- A

37-

R- A

 

38- Observe que na reação para a formação de uma molécula de glicose surgem seis moléculas de CO2  —  energia necessária  —  E=6.2,34.10-18J  —  E=1,404.10-17J  —  freqüência f da radiação eletromagnética  —  c=λf  —  3.108=6,80.10-7f  —  f=4,4.1014Hz  —  equação de Planck  —  E=n.h.f  —  n – número de fótons absorvidos  —  1,404.10-7=n.6,62.10-34.4,4.1014  —  n≈48  —  R- C

39- Observe que o pedido é a razão R entre a intensidade do campo magnético no CMS (BCMS) e do campo magnético da Terra (BTerra)  —  n=BCMS/BTerra=4/30.10-6  —  n≈133.333 vezes  —  R- A

40- a) Dado  —  Eo = 13,6 eV  —  pela conservação da energia, a energia (E) do fóton emitido é em módulo, igual à variação da energia do elétron  —  E=│Eo/22 – Eo/12│=│13,6/4 – 13,6│  —  E=10,2 e

b) Dados  —   E = 10,2 eV; 1 eV = 1,6.10-19 J  —  MP = 1,6.10-27 kg  —   c = 3.108 m/s  —  Q=E/c  —  conversão de elétron-volt para joule  —  E = 10,2 (1,6.10-19) J  —  pela conservação da quantidade de movimento, o próton adquire quantidade de movimento de mesma intensidade que o fóton, em sentido oposto  —  assim, sendo v a velocidade adquirida pelo próton  —

│Qfóton│= │Qpróton│ —  E/c=Mp.V  —  V=E/(MP.c)  —  V=10,2.1,6.10-19/1,6.10-27.3.108  —  V=3,4m/s

41- a) nágua=c/vágua  —  1,3=3.108/Vágua  —  Vágua≈ 2,3.108m/s

b)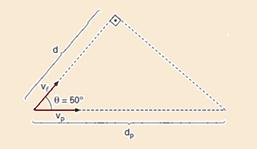

Observe na figura  —  cos50o=d/dp  —  0,64=1,6/dp  —  dp=2,5m  —  sendo a velocidade da radiação Cerenkov constante  — Vp=ΔS/Δt  —   Vp=dp/Δt  —  a radiação Cerenkov percorre a distância dp no mesmo intervalo de tempo em que a luz percorre a distância d nesse meio  —  Vp=2,5/12.10-9  — Vp≈2,1.108m/s

42- Observe a figura, que mostra o elétron movendo-se em uma de suas órbitas, sendo  —  m – massa do elétron  —  e – carga elementar – módulo da carga do próton que é igual ao módulo da carga do elétron=e  —  e – raio da órbita do elétron  —  k – constante eletrostática  —  a força eletrostática ()  trocada entre o próton e o elétron age como resultante centrípeta ()  —  Fe=FC  —  mV2/r=k.e.e/r2  —  mV2=ke2/r  —  multiplicando ambos os membros por ½  —  mV2/2 = ke2/2r (I)  —  a energia (E) do elétron é a soma da sua energia cinética (Ec) com a sua energia potencial (Ep)  —  E=Ec + Ep (II)  —  com o referencial no infinito  —  Ep= – ke2/r (III)  —  substituindo (I) e (III) em (II)  —  E=ke2/2r – ke2/r  —  E= – ke2/2r (IV)  —  de acordo com o enunciado,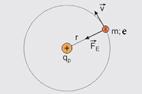

 o comprimento (C) da órbita é igual a um número inteiro (n) de comprimentos de onda (λ) do elétron  —  C=nλ  —  2πr=nλ  —  r=nλ/2π (V)  —  substituindo (V) em (IV)  —  E= – ke2/2(nλ/2π)  —  E= – kπe2/nλ

43- 

Dados  —  carga do próton  —  qp=e  —  carga do quark u  —  qu=2/3e  —  calculando a carga do quark down  —  do enunciado  —  p=u + u + d  —   qp=2qu + qd  —  e=2.(2/3)e + qd  —  e=(4/3)e + qd  —  qd= – (1/3)e  —  considere que o nêutron seja formado de x quarks up e y quarks down  —  como sua carga é nula  —  x + y = 3  —  x(2/3)e + y(-1/3)e = 0  —  2x – y = 0  —  y=2x  — X + 2x=3  —  x=1  —  y=2  —  conclui-se que um nêutron é formado de 1 quark up e 2 quarks down (n=udd)

 

44- a) Falsa  —  A fissão nuclear — divisão de um núcleo atômico pesado em dois núcleos mais leves.

b) Correta  —   Durante a fusão nuclear ocorre grande liberação de energia, já que as massas dos núcleos produzidos são inferiores as dos núcleos iniciais. Parte da massa perdida durante a fusão nuclear é convertida em energia, de acordo com a Equação de Einstein E=MC2. Estas fusões nucleares explicam o calor e a luz do Sol, percebidos por nós, aqui na Terra.

c) Falsa  —  veja b.

d) Falsa  —  veja b.

e) Falsa  —  veja b.

R- B.  

 

45-

 Veja no esquema abaixo a soma das massas dos reagentes e a soma das massas dos produtos da reação  —  diferença entre a soma dessas massas  —  ∆m=236,05 – 235,88=0,17 uma  —  equação de Einstein de equivalência entre massa e energia  —  E= ∆m.c2  —  E=0,17uma=0,17.930MeV  —  E=158,1 MeV. (essa energia é liberada principalmente sob forma de energia cinética).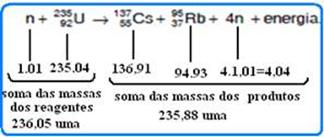

• Decaimento alfa (α) – emissão de partículas α (núcleo de 4He)  —  decaimento beta (β) – emissão, pelo núcleo, de partículas β (cargas negativas, elétrons)  —  decaimento gama (γ) – emissão de raios gama (fótons de alta energia).

46- a) Do texto  —  “Segundo todos os cálculos, as futuras usinas de fusão nuclear poderão extrair de 1 metro cúbico de água uma quantidade de energia igual à de 2 mil barris de petróleo”  —  regra de três  —  1 m3 – 2.103 barris  —  100 m3 – n barris  — 

n=2.103.102  —  n=2.105 barris de petróleo  —  como cada barril contém 1,5.106 kcal, 2.105 barris conterão  —  W=2.105 barris x

1,5.106kcal/barril  —  W=3,0.1011 kcal=3,0.1014cal  —  do enunciado  —  1 BEP (Barril Equivalente de Petróleo), equivale a 1,45.109 cal  —  regra de três  —  1 BEP – 1,45.109 cal  —  n’ BEP – 3.1014 cal  —  n’=3.1014 cal/1,45.109 cal  — 

n’≈2,07.105 BEP.

b) Do texto: “Os centros dos núcleos dos átomos de hidrogênio devem estar a 1.10-15 metros um do outro para que ocorra a fusão”  —  ainda do texto  —  “essa fusão é o processo no qual dois núcleos de átomos leves (por exemplo, o hidrogênio – cujo núcleo é constituído por 1 próton com carga elétrica elementar é 1,6.10-19C) se combinam, ou se fundem, constituindo um elemento mais pesado. Os núcleos, então, carregados positivamente, devem se aproximar suficientemente um do outro, ou seja, vencer a força de repulsão eletrostática entre eles”  —  portanto, são dados  —  d=1.10-15m  —  .|Q1|= |Q2|=1,6.10-19C  —  k=9.109N.m2/C2  —  Lei de Coulomb  —   F=k.|Q1|. |Q2|./d2 = 9.109.1,6.10-19.1,6.10-19/(1.10-15)2   —  F=23,04.101  —  F=230,4 N.

 47- 

As duas leis estabelecidas por Phillip Lenard para o efeito fotoelétrico são:

1ª Lei: para determinada frequência, o número de elétrons emitidos (conhecidos como fotoelétrons) pela placa iluminada (emissora) é proporcional à intensidade da luz nela incidente.

2ª Lei: a energia cinética dos fotoelétrons depende da frequência da radiação incidente na placa emissora, não dependendo da intensidade dessa radiação.

Como, na situação b, a intensidade da luz incidente na placa emissora é o dobro em relação à situação a, de acordo com a 1ª lei, o número de elétrons liberados também é o dobro, provocando corrente elétrica também duas vezes maior  —  ib = 2 ia  —  como se trata da mesma radiação nas duas situações (mesma frequência), a 2ª lei garante que energia cinética dos fotoelétrons também é a mesma, exigindo o mesmo potencial elétrico de frenamento (-Vo)  —  R- C

 

 Voltar para os exercícios