Resoluções comentadas dos exercícios de vestibulares sobre
Efeito Fotoelétrico
01- R- B — veja teoria
02- R- E — veja teoria
03- a) Falsa — a massa de um elétron vale aproximadamente m=9,11.10-28g.
b) Correta — veja teoria
c) Falsa — as massas dos prótons e dos nêutrons são praticamente iguais.
d) Falsa — existe a dualidade onda- partícula.
R- B
04- I- Correta — Ec=0 — W=hf — observe que a energia cedida ao elétron pelo fóton incidente é a energia que ele precisa receber para ser arrancado pelo metal
II- Falsa — a freqüência influencia (freqüência de corte – fo)
III- Falsa — a temperatura do metal não influi na emissão de elétrons.
R- E
05- Toda radiação eletromagnética (luz) se propaga de maneira descontínua em forma de “pacotes” que recebem o nome de fótons “quantum”, conceito de energia quantizada — R- 05
06– E=h.f — como h é a constante de Planck, a energia do fóton E é diretamente proporcional à freqüência f — quanto maior f, maior será E — R- A
07- R- A — veja teoria
08- R- C — veja teoria
09- Maior freqüência, maior nível de energia — a energia cinética dos fótons emitidos é a mesma e consequentemente a velocidade é a mesma — R- A
10- R- C — veja teoria
11- R- A — veja teoria
12– R- C — veja teoria
13- a) Falsa — o potencial de corte é o mesmo qualquer que seja a intensidade da luz incidente.
b) Falsa — a energia cinética máxima é fornecida por Km=e.Vo (e – carga de um elétron e Vo – potencial de corte)
c) Correta — é o fo do gráfico (freqüência de corte)
d) Falsa — Falsa — veja b
R- C
14- Você está aumentando a quantidade de fótons emitidos pela lâmpada — R- D
15- a) As energias dos fótons que surgiram foram obtidas através das massas do elétron e do pósitron que desapareceram no processo de aniquilação.A relação entre massas e energias foram previstas pela teoria da relatividade de Einstein na equação E=mC2, onde m é a quantidade de massas convertidas em energia e C a velocidade da luz no vácuo, de valor C=3,0.108ms.
b) A energia de um fóton (E) e a sua frequência (f) estão relacionadas pela expressão E = h . f, em que h é a constante de Planck — igualando as energias dos dois fótons ao equivalente em energia das massas das partículas aniquiladas (elétron e pósitron) —
Efótons = Emassas equivalentes — 2.(h.f) = 2.Melétron .C2 — 6,6.10-34.f=9,1.10-31.(3.108)2 — f=1,2.1020Hz
16- R- E — veja teoria
17- R- (01 + 02 + 04 + 16)=23 — veja teoria
18- Com o decorrer do tempo o elétron vai adquirindo mais energia o que faz aumentar a sua velocidade até que ele atinja a velocidade da luz (3,0.108m/s) e, a partir daí ele prossegue com essa velocidade que é o valor A do gráfico.
b) E=h.f — c=λf — f=c/λ — mc2=hf — mc2=hc/λ — λ=h/mc — mc=Q — 25.10-18=6.6.10-34/Q — Q=6,6.10-34/25.10-18 — Q=2,64.10-15 kg.ms
19- Quanto maior a freqüência da luz incidente (menor comprimento de onda) maior será seu nível energético facilitando a retirada de elétrons (emissão de luz) — a luz verde tema maior freqüência que a vermelha e consequentemente cada fóton verde tem mais energia que cada fóton vermelho — R- B
20- E=λf — c=λf — E=h.c/λ=6,6.10-34.3.108/600.10-9 — E=3,3.10-19J — R- C
21-
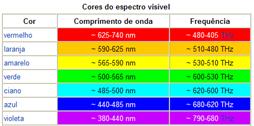
Observe na tabela ao lado que a freqüência e consequentemente o nível de energia dos fótons aumenta do vermelho para o violeta
— R- B
22- A energia da radiação incidente (fóton) é dada por E=h.f — h – constante de Planck e f freqüência do fóton incidente —
R- E
23-
R- D
24- R- E — veja teoria
25- Ecmáx=h.f – W — 3,6.1,6.10-19=6,6.10-34.f – 3.1,6.10-19 — 5,76.10-19=6,6.10-34f — f=1,6.1015 Hz — R- A
26- 01. Correta — como a freqüência da luz violeta é maior que da luz vermelha, o “fóton violeta” é mais energético que o “fóton vermelho”
02. Correta — a difração é junto com a interferência um fenômeno tipicamente ondulatório — a difração é observada quando uma onda muda de direção devido a um obstáculo cujas dimensões são comparáveis ao comprimento de onda — a interferência luminosa consiste no fato de 2 ondas, por exemplo, se movendo em sentidos contrários sofrem interferência produzindo uma onda resultante.
04. Correta — veja teoria.
08. Correta — trata-se da natureza dual da luz, ora como onda e ora como partícula.
16- Falsa — veja 08.
R- ( 01 + 02+ + 04 + 08)=15
27- E=h.f — E=m.C2 — m.C2=h.f — mC=Q=h.fC — R- C
28- As naturezas ondulatória e corpuscular da luz são complementares e não antagônicas — R- B
29- R- E
30-
31- As opções (a), (b) e (d) apresentam fenômenos exclusivamente ondulatórios. Somente a opção (b) apresenta fenômenos de características corpusculares (efeito fotoelétrico) e ondulatórias (difração)
R- C
32- Ecin.máx.=h.f – W — C=λf — f=C/λ — Ecin.máx.=h.C/λ – W=6,63.10-34.3.108/327.10-9 – 1,8.1,6.10-19 — Ecin.máx.=3,8 – 1,8 —
Ecin.máx.=2,0 eV
33- a) Do gráfico, vemos que a frequência limite, ou frequência de corte é fo = 1,2 ´ 1015Hz.
b) Dada a constante de Planck, h = 6,6 ´ 10–34 J.s — a equação de Einstein para o efeito fotoelétrico é — Ecmáx = h f – W, sendo: W o trabalho para arrancar um elétron; h.f a energia do fóton incidente e Ecmáx a energia cinética máxima com que o elétron arrancado é ejetado — veja o gráfico da energia cinética máxima em função da freqüência —
A constante h é o coeficiente angular da reta: h = tg — mas no triângulo da figura, tg a = W/fo — h =W/fo — W = h.fo —
assim a equação do efeito fotoelétrico fica — Ecmáx = h.f – h.fo = h(f – fo) — para o potencial limite de 1,5 V, podemos tirar do gráfico que a frequência é de aproximadamente 1,3.1015 Hz — efetuando os cálculos — Ecmáx = 6,6.10-34 (1,3 – 1,2) 1015 — Ecmáx=6,6.10-34 (0,1) 1015 — Ecmáx = 6,6.10-20 J.
34- A potência da luz — energia por tempo — se refere ao número de fótons que ela é capaz de emitir, por segundo — se você compara-las verificará que a mais potente (I) emite muito mais fótons por segundo que a (II) — a energia de cada fóton é fornecida por E=h.c/λ — como todas grandezas (h – constante de Planck; c – velocidade da luz e λ – comprimento de onda) são os mesmos, a energia de cada fóton também será a mesma — R- A
35- E=h.c/λ — 6.600.1,6.10-19=6,6.10-34.3.108/λ — λ=1,87.10-10m — R- E
36- a) Pela conservação da quantidade de movimento — Qantes = Qdepois — m.4.107 = m.(-V) + 14.5.106 — 4.107.m = – m.V + 7.107 — como o choque é perfeitamente elástico, devido a conservação de energia cinética, o coeficiente de restituição é igual a 1 — (velocidade relativa de afastamento)/(velocidade relativa de aproximação) = 1 — (V + 5.106)/(4.107) = 1 — V + 5.106 = 4.107 — V = 4.107 – 5.106 = 4.107 – 0,5.107 = 3,5.107 m/s — voltando na expressão da conservação da quantidade de movimento — 4.107.m = – m.V + 7.107 — 4.107.m = – m.3,5.107 + 7.107 — 4.107.m + 3,5.107.m = 7.107 — 7,5.m = 7 — m = 7/7,5 — m=0,93 u (unidade de massa atômica)
b) Pela expressão da energia E = hc/l — 7.1012 = 4.10-15.3.108/l — l = 12.10-7/(7.1012) — λ=1,7.10-19 m
37- A cor é uma característica da luz absorvida e da luz refletida pelos objetos, dependendo ainda da luz incidente sobre eles.
R- E
38- (I) Correta — conforme propôs Einstein, a luz é formada de corpúsculos ou quanta de luz, mais tarde denominados fótons — de acordo com a equação de Planck, a energia (E) transportada por um fóton é diretamente proporcional à frequência (f) da radiação — E = h f, sendo h a constante de Planck.
(II) Correta.= — Ecmáx=hf – W — sendo W o trabalho para arrancar um elétron do metal.
(III) Incorreta.
R- C
39- Sendo a velocidade do elétron é muito menor que a velocidade da luz, pode-se desconsiderar efeitos relativísticos e usar a expressão convencional da energia cinética. — Ec = h f e Ec =mV2/2 — combinando essas expressões —
h f = mV2/2 — f=mV2/2h=9,11.10-31.(3.107)2/2.6,6.10-34=8,2.10-16/13.10-33 — f=6,3.1017 Hz — a ordem de grandeza é 1018
40- a) Dados: c = 3.108 m/s; h = 6.10-34 J.s; l = 6.10-7 m.
Lembrando a equação fundamental da ondulatória:
c = l f — f =c/λ — substituindo essa expressão na equação dada — E = h f — E = hc/λ — E = 3.10-19 J.
b) Dados: i = 45°; r = 30°; nar = 1.
Aplicando a Lei de Snell — nar sen 45° = nX sen 30° — 1.√2/2=nX.1/2 — nX=√2
nX =
c) Dados: c = 3.108 m/s — da definição de índice de refração — nX=c/VX — VX=c/nX=3.108/√2 — VX=1,5.√2.108 m/s
41- A física clássica estabelecia que a luz se propagava na forma de ondas e de maneira contínua — a física moderna estabeleceu a teoria quântica, afirmando que a luz não se propaga de forma contínua, mas em pequenos “grânulos” chamados fótons — ao movimento de cada partícula está associada uma onda — dependendo do fenômeno, prevalecem as características ondulatórias ou corpusculares, daí a dualidade entre partículas e ondas.
Por exemplo: quando se faz um feixe de elétrons atravessar uma fenda, ocorre difração, evidenciando o caráter ondulatório da matéria — quando um feixe de luz de alta frequência incide sobre uma chapa metálica, elétrons podem ser arrancados (efeito fotoelétrico) explicado por Einstein, considerando a luz como um feixe de partículas.
R- C
42-
43- a) m1 = m2 = 2 g = 2.10-3 kg; c = 3.108 m/s — a massa a ser convertida em energia é m = m1 + m2 = 4.10-3 kg — da equação de Einstein, a energia liberada na aniquilação é — Elib = mc2 — Elib = 4.10-3.(3.108)2 — Elib = 4.10-3.9.1016 — Elib=3,6.1014 J
b) Dados — população — 1 milhão de habitantes — N = 106 habitantes — consumo médio — 100 kWh/habitante.mês —
lembrando que 1 kWh = 3,6.106 J, a potência consumida mensalmente pela cidade é: — Potcons = 100.106.3,6.106 = 360.1012 — Potcons=3,6´1014 J/mês — Potcons=Elib/Δt — 3,6.1014=3,6.1014/Δt — Δt=1 mês
44- R- A
45- Energia de um fóton — E=h.f — energia transformada por n fótons — Etotal=nh.f=400h.f — c=λ.f — E=h.c/λ — potência — Po=Etotal/Δt — Po=400h.c/λ.Δt (I) — intensidade de onda que deve impressionar a retina — I=Po/A=Po/π.d2(II) — substituindo I em II — I=400h.c/π.r2λΔt (III) — intensidade de onda da fonte — I=Pof/4πd2 (IV) — igualando III com VI — 400h.c/π.r2λΔt= Pof/4π.d2 — d=r/400.√(Pof.λ.Δt)/h.c — observe que, sendo r, Pof, Δt,h e c constantes, a distância d é diretamente proporcional ao comprimento de onda λ — como o comprimento de onda da luz vermelha (lv) é maior que o da luz azul (la), a fonte que poder ser vista a uma distância maior é a que emite luz vermelha.
46- Respostas das questões que envolvem física:
01) Falsa — os átomos têm a capacidade de emitir luz no exato momento em que elétrons saltam de camadas mais externas para outras mais internas da eletrosfera atômica.
02) Falsa — lentes de bordas grossas com índice de refração maior que o do ar são divergentes.
16) Falsa — 1 quatrilhão = 1015 — duração do pulso — ∆t=1/1015 — ∆t=10-15 s
R- (04 + 08 + 64) = 76.
47- P=E/∆t — 110.10-3=E/6.10-9 — Etotal=660.10-12J — E1fóton=hf=6,6.10-34.4.1014 — E1fóton=26,4.10-20J — número de fótons — n=Etotal/E1fóton=660.10-12/26,4.10-20 — n=25.108=2,5.109 — R- A
48- Equação fundamental da ondulatória — V=c=λf — 3.108=700.10-9.f — f=3/7.1015Hz — Etotal=500kcal=5.105 cal=5.105.4 — Etotal=2.106 J — E1fóton=hf=6,62.10-34.3/7.1015 — E1fóton=2,9.10-19J — número de fótons — n=Etotal/E1fóton=2.106/2,9.10-19 — n=0,69.1025=6,9.1024 — R- A
49- a) Dados — λverde = 500 nm — λvermelho = 650 nm — equação fundamental da ondulatória — c=λv — v=λ/c (I) — equação de Plank — E=hv (II) — relacionando (I) com (II) — E=hc/λ — razão pedida — R=Evermelho/Everde=(hc/λvermelho)/(hc/λverde) — R=Evermelho/Everde=λvermelho/λverde=650/500 — R=1,3
b) Dados — h = 6,6.10-34 J.s — m = 5.10-26 kg — λ = 660 nm = 6,6.10-7 m — a variação da quantidade de movimento do átomo é igual à quantidade de movimento do fóton — ∆Qátomo=pfóton — m.∆Vátomo=h/λ — ∆Vátomo=h/λm=6,6.10-34/6,6.10-7x
5.10-26=0,92 — ∆Vátomo=2,0.10-2m/s
50- As duas leis estabelecidas por Phillip Lenard para o efeito fotoelétrico são:
1ª Lei: para determinada frequência, o número de elétrons emitidos (conhecidos como fotoelétrons) pela placa iluminada (emissora) é proporcional à intensidade da luz nela incidente.
2ª Lei: a energia cinética dos fotoelétrons depende da frequência da radiação incidente na placa emissora, não dependendo da intensidade dessa radiação.
Como, na situação b, a intensidade da luz incidente na placa emissora é o dobro em relação à situação a, de acordo com a 1ª lei, o número de elétrons liberados também é o dobro, provocando corrente elétrica também duas vezes maior — ib = 2 ia — como se trata da mesma radiação nas duas situações (mesma frequência), a 2ª lei garante que energia cinética dos fotoelétrons também é a mesma, exigindo o mesmo potencial elétrico de frenamento (-Vo) — R- C
51-
01- 01.Correta — A figura abaixo mostra o gráfico da energia cinética do elétron extraído em função da frequência da radiação (fóton, cor) incidente, para uma mesma placa metálica (célula fotoelétrica).
fo é a freqüência mínima (frequência de corte) necessária para produzir o efeito fotoelétrico. Se f=fo o elétron é liberado, mas sua energia cinética é nula. Para freqüências inferiores a fo o fenômeno não ocorre. Porém, para valores superiores a fo, o número de elétrons arrancados é diretamente proporcional à intensidade da radiação eletromagnética incidente, ou seja, aumentando a intensidade da radiação (freqüência, cor) incidente no metal, aumenta-se o nível energético dos fótons incidentes, aumentando assim número de elétrons arrancados.
02. Correta — veja 01.
04. Falsa — à medida que a freqüência (cor, nível energético) da radiação incidente aumenta, a energia cinética dos elétrons emitidos também aumenta. Mas, para a mesma freqüência f (cor, nível energético) a energia cinética dos elétrons emitidos é sempre a mesma.
08. Correta — Foi Albert Einstein que explicou corretamente o efeito fotoelétrico em 1921, recebendo por isso o prêmio Nobel da Física. Segundo Einstein a energia de qualquer radiação luminosa (inclusive luz) não se espalha uniforme e continuamente pelo espaço mas, sim, concentrada em pequenos “pacotes”que carregam uma quantidade bem definida de energia. Cada um desses pacotes é denominado quantum de energia e esse modelo construído por Einstein recebeu o nome de teoria dos quanta. Quanta, em latim é plural de quantum, que significa “quantidade”.
Esses quanta de energia radiante foram denominados de fótons.
16. Falsa — Essa energia mínima para extrair um elétron da placa metálica é denominada função trabalho e está relacionada com o tipo de metal utilizado e depende da frequência da radiação incidente.
Corretas:01,02 e 08 — soma 11.
52-
A correta numeração dos parênteses, de cima para baixo, é
A) 1 – 2 – 3 – 4 – 5
B) 2 – 1 – 4 – 3 – 5
C) 3 – 2 – 5 – 4 – 1
D) 4 – 3 – 5 – 2 – 1
E) 5 – 2 – 1 – 4 – 3
A expressão E=h.f afirma que quanto maior a frequência maior é a energia do fóton — observe nas tabelas abaixo que a freqüência e consequentemente o nível de energia dos fótons aumenta do vermelho para
o violeta e das ondas de rádio para os raios gama — R- C.
53-
As duas leis estabelecidas por Phillip Lenard para o efeito fotoelétrico são:
1ª Lei: para determinada frequência, o número de elétrons emitidos (conhecidos como fotoelétrons) pela placa iluminada (emissora) é proporcional à intensidade da luz nela incidente.
2ª Lei: a energia cinética dos fotoelétrons depende da frequência da radiação incidente na placa emissora, não dependendo da intensidade dessa radiação.
Como, na situação b, a intensidade da luz incidente na placa emissora é o dobro em relação à situação a, de acordo com a 1ª lei, o número de elétrons liberados também é o dobro, provocando corrente elétrica também duas vezes maior — ib = 2 ia — como se trata da mesma radiação nas duas situações (mesma frequência), a 2ª lei garante que energia cinética dos fotoelétrons também é a mesma, exigindo o mesmo potencial elétrico de frenamento (-Vo) — R- C
54-
A) A emissão de elétrons devido à radiação incidente sobre o emissor surge quase que instantaneamente, independente se a radiação (luz) incidente tiver baixa intensidade — o atraso entre o tempo de incidência da iluminação e o tempo de emissão dos elétrons é da ordem de 10-9 s (praticamente instantâneo) — esse comportamento se justifica pelo modelo corpuscular da luz, proposto por Einstein — a radiação é formada por pequenos pacotes de energia (fótons) que, ao colidirem diretamente com um dos elétrons da superfície, transmite instantaneamente toda sua energia para o elétron — então, ele é arrancando-o, imediatamente da superfície.
B) O efeito fotoelétrico só surge se o metal receber um feixe de radiação com energia superior à energia mínima de remoção dos elétrons do metal, provocando a sua saída das órbitas o que pode ocorrer sem energia cinética (se a energia da radiação for igual à energia de remoção) ou com energia cinética, se a energia da radiação exceder a energia de remoção dos elétrons.
Essa energia mínima para extrair um elétron da placa metálica é denominada função trabalho e está relacionada com o tipo de metal utilizado. Se a energia do fóton que incide (h.f) for maior que a função trabalho (W) a energia em excesso será energia cinética (Ec), de modo que — W=h.f – Ec — denominada equação fotoelétrica de Einstein..
C) A figura abaixo mostra o gráfico da energia cinética do elétron extraído em função da frequência da radiação (fóton, cor) incidente, para uma mesma placa metálica (célula fotoelétrica).
Fo é a freqüência mínima (frequência de corte) necessária para produzir o efeito fotoelétrico. Se f=fo o elétron é liberado, mas sua energia cinética é nula. Para freqüências inferiores a fo o fenômeno não ocorre. Porém, para valores superiores a fo, o número de elétrons arrancados é diretamente proporcional à intensidade da radiação eletromagnética incidente, ou seja, aumentando a intensidade da radiação (freqüência, cor) incidente no metal, aumenta-se o nível energético dos fótons incidentes, aumentando assim número de elétrons arrancados.
55-
I. Correta — Quando a luz interage com a matéria através de absorção, emissão, choques, etc., ela se comporta como partícula (modelo corpuscular), mas para os fenômenos referentes à sua propagação, reflexão, refração, interferência, etc., ela se comporta como onda.
II. Correta — A figura abaixo mostra o gráfico da energia cinética do elétron extraído em função da frequência da radiação (fóton, cor) incidente, para uma mesma placa metálica (célula fotoelétrica).
Fo é a freqüência mínima (frequência de corte) necessária para produzir o efeito fotoelétrico. Se f=fo o elétron é liberado, mas sua energia cinética é nula. Para freqüências inferiores a fo o fenômeno não ocorre. Porém, para valores superiores a fo, o número de elétrons arrancados é diretamente proporcional à intensidade da radiação eletromagnética incidente, ou seja, aumentando a intensidade da radiação (freqüência, cor) incidente no metal, aumenta-se o nível energético dos fótons incidentes, aumentando assim número de elétrons arrancados.
III. Falsa — A emissão e a energia dos elétrons arrancados dependem da freqüência e não da intensidade da radiação eletromagnética incidente.
R- D
56-
As duas leis estabelecidas por Phillip Lenard para o efeito fotoelétrico são:
1ª Lei: para determinada frequência, o número de elétrons emitidos (conhecidos como fotoelétrons) pela placa iluminada (emissora) é proporcional à intensidade da luz nela incidente.
2ª Lei: a energia cinética dos fotoelétrons depende da frequência da radiação incidente na placa emissora, não dependendo da intensidade dessa radiação.
Como, na situação b, a intensidade da luz incidente na placa emissora é o dobro em relação à situação a, de acordo com a 1ª lei, o número de elétrons liberados também é o dobro, provocando corrente elétrica também duas vezes maior — ib = 2 ia — como se trata da mesma radiação nas duas situações (mesma frequência), a 2ª lei garante que energia cinética dos fotoelétrons também é a mesma, exigindo o mesmo potencial elétrico de frenamento (-Vo) — R- C