Resolução Comentada da UEM 2015
RESOLUÇÕES
01- 01) Pressão é uma grandeza vetorial, portanto tem módulo, direção e sentido definidos
01. Falsa 
Se a força 
estiver inclinada de um ângulo β em relação à horizontal, a parcela dessa
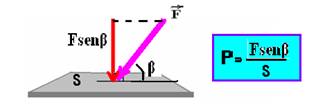
força que exerce a pressão é a componente vertical de 
, ou seja, é Fsenβ, conforme a figura acima.
A pressão sempre vai estar relacionada ao módulo da força que age perpendicularmente à superfície. Então não importa a direção que a força é aplicada, ela não muda a direção da pressão, que é sempre perpendicular a superfície.
Só o que leva em conta na pressão, portanto, é a intensidade.
02) A diferença de pressão entre dois pontos no interior de um líquido homogêneo e em equilíbrio é
proporcional à diferença de profundidade entre esses dois pontos.
02. Correta Teorema de Stevin Observe a figura abaixo onde, quem varia é apenas a pressão vertical, onde o líquido que é homogêneo e incompressível está em equilíbrio.
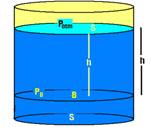
Na superfície livre superior (A) desse líquido age a pressão atmosférica (Patm), exercida pela coluna de ar que está sobre ele. Num ponto qualquer B do interior do líquido, a pressão (PB) que age é a soma da pressão atmosférica com a pressão exercida pela coluna líquida acima dele, devido à seu peso.
PB=Patm + Plíquido — PB=Patm + F/S — PB= Patm + peso do líquido/S — PB=Patm + (mlíquido.g)/S — dlíquido=mlíquido/Vlíquido — dlíquido=mlíquido/S.h — mlíquido=dlíquido.S.h — PB=Patm + (dlíquido.S.h)/S — PB=Patm+ dlíquido.g.h — esta expressão é chamada de Teorema Fundamental da Hidrostática ou de Teorema de Stevin
04) No sistema internacional de medidas (SI) a unidade de pressão é o Pascal (Pa).
04. Correta Pa = N/m2.
08) Quando um dado ponto de um líquido em equilíbrio no interior de um recipiente sofre uma variação de pressão, essa variação de pressão é transmitida a todos os pontos do líquido e das paredes do recipiente.
08. Correta Considere um fluido (líquidos e gases que fluem para as regiões inferiores de um recipiente até preenchê-los totalmente) em equilíbrio (vertical e horizontal) no interior de um recipiente.
Esse líquido exerce sobre as paredes do recipiente que o contem forças que se tornam de maior intensidade à medida que a profundidade aumenta.
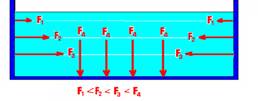
Observe que as forças, na mesma horizontal, em ambos os extremos, tem a mesma intensidade, pois o líquido está em equilíbrio horizontal, caso contrário, ele se moveria nessa direção.
16) Estando um líquido em um recipiente aberto, a pressão na superfície do líquido é nula.
16. Falsa veja 02.
R- (02 + 04 + 08) = 14
02- Toda a teoria que envolve as fórmulas fornecidas encontram-se em fisicaevestibular.com.br – Mecânica – Dinâmica – MHS – Sistema massa-mola.
01) A amplitude máxima de oscilação do sistema massa-mola é de 20 cm.
01. Falsa a amplitude A é fornecida pelo enunciado Quando o sistema é trazido para a posição +10 cm em relação à posição de equilíbrio A = 10 cm.
02) A velocidade angular de oscilação do sistema massa-mola é de 20 rad/s.
02. Correta W = √(k/m = √(80/0,2) = √400 W = 20 rad/s.
04) O período de oscilação do sistema massa-mola é de π/10 s.
04. Correta T=2π√(m/k) = 2π√(0,2/80) = 2π√(0,2/80) = 2π√(0,0025) T = 2π(0,05) = π.0,01 = π/10 s.
08) A aceleração do bloco quando ele passa sobre o ponto x = -0,2 cm é de 2 m/s2.
08. Falsa a= -k/m.x = – 80/0,2.(-0,02) a = 8 m/s2.
16) A frequência de oscilação do sistema massa-mola é de aproximadamente 6,28 Hz.
16. Falsa f = 1/T = 1/(π/10) f = 10/π = 10/3,14 = 3,184 Hz.
R- (02 + 04) = 06
03- 01) A variação da energia interna de um sistema físico é dada pela diferença entre o calor trocado com o meio externo ao sistema e o trabalho realizado no processo termodinâmico.
01. Correta O Primeiro Princípio da Termodinâmica (Princípio da Conservação da Energia) afirma que: “A energia não pode ser criada nem destruída, mas apenas transformada”
Suponha que um sistema isolado receba 300J de calor. Se, por exemplo, 50J dessa energia forem absorvidos pelo sistema, então a parte restante, 250J, será fornecida ao ambiente sob a forma de trabalho.
Então, Q= W + ΔU ou,
A expressão acima é a representação matemática do primeiro princípio da termodinâmica.
02) A energia interna de uma dada quantidade de gás perfeito é função exclusiva da temperatura desse gás.
02. Correta Energia interna de um gás perfeito
A energia interna (U) de um gás perfeito monoatômico corresponde a soma das energias cinéticas médias (Ec) de todas as suas moléculas e, pela lei de Joule é fornecida por:
A afirmação acima indica que a temperatura de um gás é a medida da energia cinética média de suas moléculas.
04) As transformações termodinâmicas naturais sempre levam à conservação da quantidade de movimento e da entropia do Universo.
04. Falsa.
08) Dois corpos, em equilíbrio térmico, possuem a mesma temperatura e, nessa condição, não há troca de calor entre eles.
08. Correta só existe troca de calor entre dois corpos quando eles estiverem à temperaturas diferentes e essa transferência ocorre sempre do corpo de maior para o de menor temperatura.
16) Se dois ou mais corpos trocam calor entre si até atingirem o equilíbrio termodinâmico, a soma
algébrica das quantidades de calor trocada é sempre positiva e será tanto maior quanto maior a
temperatura inicial desses corpos.
16. Falsa a quantidade de calor é negativa para o corpo que cede calor e positiva para o que recebe calor.
R- (01 + 02 + 08) = 11
04- 01) Condutores elétricos paralelos percorridos por correntes elétricas que fluem no mesmo sentido
repelem-se.
01. Falsa Força de interação entre dois fios condutores paralelos
Considere dois condutores retilíneos 1 e 2 percorridos, respectivamente por correntes elétricas i1 e i2, e separados por uma distância d. Tem-se duas situações:
As correntes elétricas tem mesmo sentido
Utilizando a regra da mão direita, você determina 
que é o vetor indução magnética que o condutor 1 produz onde está o condutor 2.
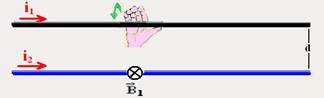
O condutor 2, imerso no campo magnético de ficará sujeito a uma força magnética 
, fornecida pela regra da mão esquerda.
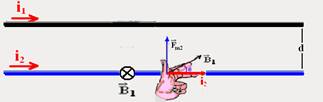
Assim, o condutor 2 fica sujeito a uma força magnética 
vertical e para cima.
Analogamente, o condutor 2 origina, onde está o condutor 1, um campo magnético 
, que, fornecido pela regra da mão direita estará saindo da folha de papel. Então surgirá sobre o condutor 1 uma força vertical e para baixo, fornecida pela regra da mão esquerda.
Situação final:
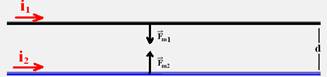
Dois fios condutores retilíneos, paralelos e próximos um do outro, sofrem forças de atração se as correntes que os percorrem tiverem mesmo sentido.
Se as correntes elétricas tiverem sentidos contrários, procedendo da mesma forma que no item anterior, você observará que os dois fios sofrem força de repulsão.
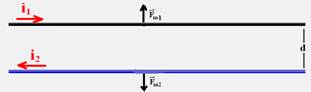
Dois fios condutores retilíneos, paralelos e próximos um do outro, sofrem forças de repulsão se as correntes que os percorrem tiverem sentidos contrários.
02) A força eletromotriz induzida em uma espira condutora é diretamente proporcional à variação
temporal do fluxo magnético que atravessa essa espira.
02. Correta “ O módulo da força eletromotriz induzida num circuito é igual à razão entre a variação do fluxo magnético nesse circuito, pelo intervalo de tempo em que essa variação ocorre”
Eventualmente, devido à lei de Lenz, que afirma que a força eletromotriz induzida se opõe à variação de fluxo, costuma-se escrever a lei de Lenz da seguinte forma:
04) A força eletromotriz induzida em uma espira condutora é inversamente proporcional ao intervalo
de tempo em que ocorre a variação do fluxo magnético que atravessa a espira.
04. Correta observe na expressão ε = ∆Ф/∆t que ε é inversamente proporcional a ∆t.
08) A corrente elétrica induzida em um circuito elétrico produz um campo magnético que permite o aumento do fluxo magnético que a induz.
08. Falsa Poe produzir também uma diminuição do fluxo magnético.
16) A variação temporal do campo magnético em uma determinada região do espaço provoca o
aparecimento de um campo elétrico variável nessa mesma região.
16. Correta
R- (02 + 04 + 16) = 22
05- 01) No gráfico da intensidade da força em função do tempo, a área sob a curva é numericamente igual ao impulso da força.
01. Correta Em todo gráfico força X tempo, a intensidade do impulso é fornecida pela área
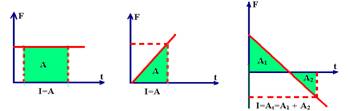
compreendida entre a reta representativa e o eixo do tempo, no intervalo pedido.
02) A variação do momento linear de um ponto material é igual ao impulso da força resultante que atua sobre ele
02. Correta Teorema do Impulso “O impulso da força resultante de um sistema de forças que age
sobre um corpo é igual à variação da quantidade de movimento do corpo”
04) Em um sistema isolado, no qual a resultante das forças que atuam sobre esse sistema é nula, o
momento linear permanece constante.
04. Correta Quando um sistema é isolado de forças externas, sua força resultante tem intensidade nula e consequentemente o impulso dessa força é nulo, pois I=FR.∆t=0. ∆t=0. Como I = Qdepois – Qantes — 0= Qdepois – Qantes — Qantes = Qdepois. Sendo a quantidade de movimento grandeza vetorial, a relação abaixo representa o princípio da conservação da quantidade de movimento (momento linear):
08) Quando dois automóveis colidem e se deslocam juntos após a colisão, temos uma colisão
perfeitamente elástica na qual o momento linear total diminui.
08. Falsa Independente do tipo de choque, a quantidade de movimento (momento linear) sempre se conserva em módulo, direção e sentido.
16) Em qualquer tipo de colisão, o momento linear é conservado, mantendo-se constantes seu módulo, sua direção e seu sentido.
16. Correta veja 08.
R- (01 + 02 + 04 + 16) = 23
06- 01) Os resistores equivalentes nos dois ramos do circuito possuem, respectivamente, resistência elétrica de 30 Ω e de 5 Ω.
01. Correta ramo A série Req = 10 + 10 + 10 = 30 Ω ramo B paralelo Req = 10.10/(10 + 10) = 100/20 Req = 5 Ω.
02) A corrente elétrica que flui no ramo A é de 2 A.
02. Falsa Req = U/i 30/7 = 10/i i = 2,33 A iA = 10/30 = 0,33 A iB = 10/5 = 2 A.
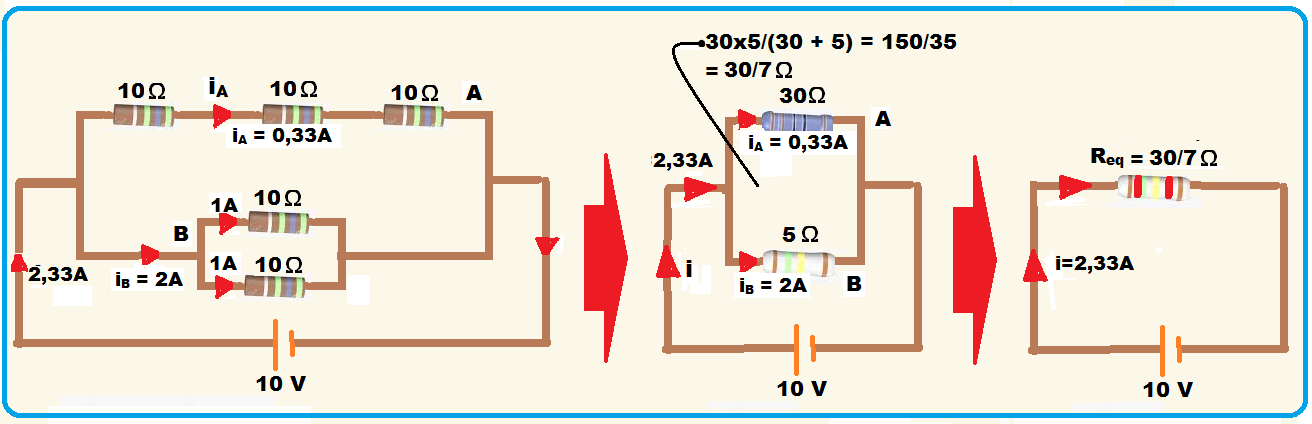
Veja acima que iA = 0,33 A.
04) A potência dissipada no ramo B é de 20 W.
04. Correta P = R.iB2 = 5.22 = 20 W.
08) A potência dissipada e a corrente elétrica no ramo B são maiores que as observadas no ramo A.
08. Correta de 04, PB = 20W PA = R.iA2 = 30.0,33 = 9,9 W.
16) A diferença de potencial entre os terminais do segundo resistor do ramo A é de aproximadamente 3,3 V
16. Correta R = U/iA 10 = U/0,33 U = 3,3 V.
R- (01 + 04 + 08 + 16) = 29
07- 01) A velocidade com que o bloco percorre a superfície delgada, plana e horizontal é A √(2ghA) , sendo g a aceleração da gravidade.
01. Correta cálculo da velocidade com que o bloco chega à base C pela conservação da energia mecânica já que não existe atrito e o sistema é conservativo.
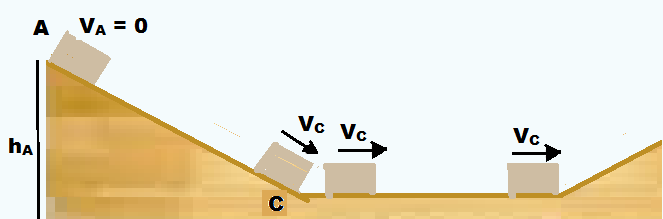
EmA = MVA2/2 + MghA = M.02/2 + Mgh = Mgh.
EmC = MVC2/2 + MghC = M.VC2/2 + Mg.0 = MVC2/2.
EmA = EmC MghA = MVC2/2 VC =√(2ghA). Essa é a velocidade com que ele chega à base do plano inclinado e, como não existe atrito, é a mesma com que ele percorre o plano horizontal.
02) O trabalho realizado pela força peso sobre o bloco, durante seu movimento na superfície do plano inclinado A, é A mgh .
02. Correta Wpeso = P.d.cos90o = P.d.0 = 0
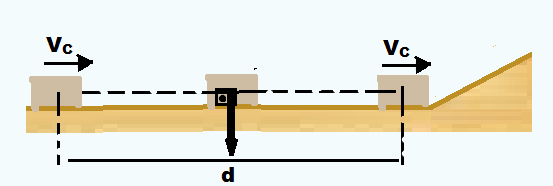
04) O trabalho realizado pela força peso sobre o bloco, durante seu movimento na superfície do plano inclinado B, é B mghB.
04. Falsa EmC = MVc2/2 + MghC = M.(√(2ghA)2/2 + M.g.0 = MghA.
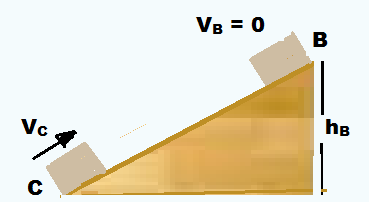
EmB = MVB2/2 + MghB = M.02/2 + MghB = MghB.
WCB = EmB – EmC = MghB – MghA = Mg(hB – hA)
08) A quantidade de movimento do bloco é conservada somente quando o bloco se movimenta na superfície horizontal, onde a somatória de forças sobre o mesmo é nula.
08. Correta Q = M.V e, como M e V nesse trecho são os mesmos a quantidade de movimento Q também é a mesma.
16) O trabalho líquido realizado pela somatória de forças que agem sobre o bloco durante seu deslocamento sobre o plano inclinado B é –dB.(FatB + Mgsenθ), sendo θ o ângulo de inclinação do plano inclinado B, g a aceleração da gravidade e FatB a força de atrito entre a superfície do bloco e a
superfície do plano inclinado B.
16. Correta
R- (01 + 02 + 08 + 16) = 27
08- 01) No instante t = 3 s, a velocidade do móvel B é nula.
01. Correta equação da velocidade do móvel B VoB = 12 m/s e aB = – 4 m/s2 VB = VoB + aBt = 12 – 4t quando t = 3 s, VB = 12 – 4.3 = 12 – 12 = 0.
02) No instante t = 4 s, os dois móveis se encontram
02. Correta no encontro XA = XB 25 – 3t + 3t2 = 45 + 12t – 2t2 5t2 – 15t – 20 = 0 ∆ = 225 – 4.5.(-20) ∆ = 625 √∆ = 25 t = 15 ± 25/10 t1 = 40/10 = 4s e t2 < 0.
04) A distância percorrida pelo móvel B, do instante t = 0 s até quando ele se encontra com o móvel A, é de 25 m
04. Falsa substituindo t = 4s em XB = 45 + 12.3 + 2.16 = 113 m ∆XA = 113 – 45 = 68 m
08) Entre os instantes t = 0 s até quando o móvel B se encontra com o móvel A, a velocidade média desse móvel é de 4 m/s.
08. Correta
16) A função horária da velocidade relativa entre os móveis A e B é dada por VAB (t) = – 15 + 10t , em que VAB = VA – VB, sendo VA e VB as velocidades dos móveis A e B, respectivamente.
16. Correta VA = – 3 + 6t VB = 12 + 4t VAB = VA – VB = -3 + 6t – 12 + 4t = -15 + 10t.
R- (01 + 02 + 08 + 16) = 27