VECTORS – VECTOR KINEMATICS – RESOLUTION
Commented Resolution
Vectors – Vector Kinematics
01- The graphic scale states that each centimeter of the map is equivalent to 250 kilometers of terrain,
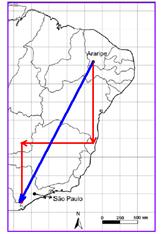
which makes it easier to represent the path taken by the traveler in vector form and even to represent his vector displacement (in blue). In this way, he walked 1000 km to the South (an easy direction to identify, since the North is indicated on the map), leaving Ceará and passing through Pernambuco and Bahia. In this state, he changed course and traveled 1,000 km to the West, arriving in Goiás, from where he headed another 750 km to the South, arriving in the state of São Paulo. On this route, the traveler saw the ecosystems of the Caatinga, the Cerrado and the Atlantic Forest.
R- And
02- Observe the sequence below:
R-D
03- Adding all vectors using the polygonal line method
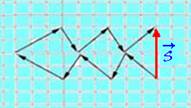
S=4.0,50=2.0cm — R- E
04-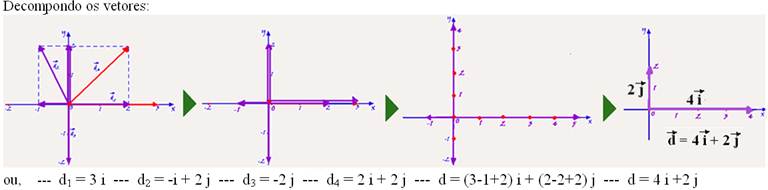
or even, adding the vectors using the polygonal line method — note that they are in the sequence 0,1,2, 3 and 4.
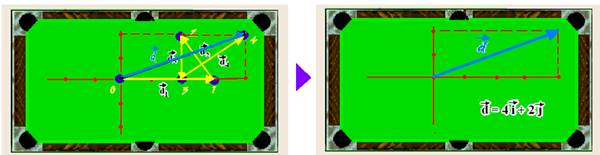
R-D
05- Since the distance between the two buoys does not vary, they are stationary in relation to each other. So, the boy must swim directly from one to the other — A- A
06- As the ocean liner moves in a straight line at constant speed, it is in dynamic equilibrium and behaves as if it were at rest (static equilibrium), not affecting the movement of the ball — R- D
07- Data: v car = 80 km/h; senθ = 0.8 and cosθ = 0.6 — the figure below shows the car and the
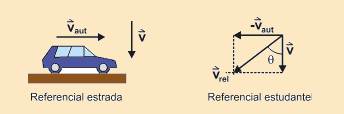
speeds of the car ( 
) and the rain ( 
), for the person standing on the side of the road. The vector diagram shows the composition of these speeds for the student — tanθ =V car /V — senθ/cosθ=V car /V — 0.8/0.6=80/V car — V car =60km/h — R- B
08- The crossing time depends only on the width of the river (L) and the speed of the boat in relation to the banks (u) — u=L/t — t=L/u — the higher the speed of the water, the greater the displacement of the boat to the right — R- B
09- When the car is moving to the right, the raindrops that would fall vertically if the car was stopped, are tilted to the left — R- B