Energia Mecânica – Resolução
Resolução Comentada
Transformações de Energia – Energia Mecânica
01- Observe que na figura I ele está correndo (energia cinética) no solo horizontal sem utilizar a vara (energia elástica) e nem subir (energia gravitacional), então, em I você identifica apenas energia cinética — na figura II ele está se movendo (energia cinética),
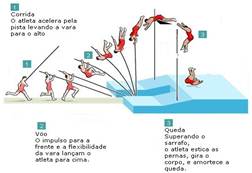
a flexibilidade da vara o impulsiona para cima (energia elástica) e ele está ganhando altura (energia gravitacional) — na figura 3 ele está se movendo para baixo (energia cinética), perdendo altura (energia gravitacional) e não havendo energia elástica (abandonou a vara) — R- C
02- Observe pelo enunciado que não há perda de energia mecânica por atrito, então o sistema é conservativo — no instante em que o carrinho deixa a mola com velocidade v, toda sua energia potencial elástica armazenada (kx2/2) se transforma em energia cinética (mv2/2) — kx2/2=mV2/2 — 8000.(2.10-2)2/2=0,2.V2/2 — V2=32.10-1/2.10-1=16 — V=4,0m/s
Ao iniciar a subida da rampa o carrinho tem energia cinética Ec=mv2/2=0,2.42/2=1,6J — essa energia na altura h onde a velocidade é de 2,0m/s se transforma em cinética e potencial gravitacional — 1,6=mv2/2 + mgh — 1,6=0,2.22/2 + 0,2.10.h — 1,6 – 0,4=2h — h=0,6m — R- E
03- Antes do salto a única energia existente é a energia cinética (com o nível zero de altura no ponto 0,8m) — Emsolo=m.V2/2 — na altura máxima só tem energia potencial gravitacional — Emhmáx=m.g.h=m.10.3,2=32m — como não há dissipação de energia elas são idênticas — Emsolo= Emhmáx — m.V2/2=32m — V2/2=32 — V=8m/s — R- D
04- A energia total do corpo na altura de 10m, que é só a gravitacional (a cinética é zero, abandonado do repouso) vale Em=mgh=2.10.10 — Em=200J — ao chegar ao solo (a gravitacional é nula, altura nula), a parte de energia que é transformada em cinética vale — Em=200 – 4 — Em= 196J — Em=mV2/2 — 196=2V2/2 — V=√196 — V=14m/s — R- B
05- Dados: r = 80 cm = 0,8 m; h = 2 m; m = 36 kg; H = 6 m e g = 10 m/s2 — como na descida o atrito é desprezível, o sistema pode ser considerado conservativo — então, tomando como referência o plano que contém o final do toboágua, pela conservação da energia mecânica — na altura de 6m quando a criança parte do repouso (V=0, Ec=0), só existe energia potencial gravitacional — Emi=mgH — quando ela chega à altura de 2m ela terá energia cinética e energia potencial — Emf=mgh + mV2/2 — Emi=Emf — m g H = m g h + mV2/2 — 10.(6) = 10.(2) + V2/2 — v2 = 80 — a
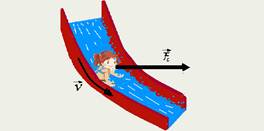
força horizontal de intensidade Fh sobre a criança na altura de 2m, quando V2=80 é a força resultante centrípeta — Fc=Fh=mV2/R=36×80/0,8 — Fh=3.600N
Fx = Fc = mV2/R= 36×80/08 — Fx = 3.600 N.
R- C
06- Vamos supor que seja no ponto X que a formiga perca contato com a bola — nesse ponto, a reação normal 
deixa de existir agindo sobre a formiga somente seu peso 
, que tem como componente a força resultante centrípeta, dirigida para o centro da circunferência e de intensidade FRC=m.Vx2/R — observe no triângulo menor — cosα=FRC/P — FRC=Pcosα=mgcosα —
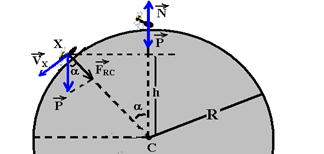
mgcosα=mVx2/R — gcosα=Vx2/R (I) — observe no triângulo maior – cosα=h/R, que substituído em (I) — g.h/R=Vx2/R — Vx2=g.h — Vx=√(gh).
Chamando a posição inicial da formiga de Y e considerando a horizontal que passa por X como nível zero de altura (figura abaixo):
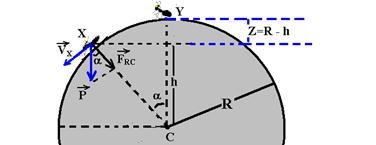
EmY=Ecy + Epy =0 + mg.(R-h) — Emy=m.g.(R-h) — Emx=Ecx + Epx=m.Vx2/2 + 0 — Emx=m.Vx2/2 — Emy=Emx — m.g.(R-h)=m.Vx2/2 — Vx2=2.g.(R-h) — que substituído em Vx2=g.h — g.h=2.g.R – 2.g.h — 3h=2R — h=2R/3.
R- A
07- Como o sistema é conservativo a energia mecânica total é constante e diferente de zero (gráfico III) — se a energia total é constante quando a energia potencial diminui a cinética deve aumentar ou quando Ep = máxima, Ec =0 (gráfico I).
R- B
08- Observe a figura abaixo que mostra os pontos de velocidade nula (A) e de velocidade máxima
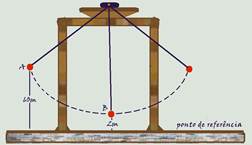
(B) — pela conservação da energia mecânica — EmA=EmB — 3mghA=3mghB + 3mV2/2 — g(hA – hB)=V2/2 — V2=20.(60 – 2)=1.160 — V=√(1.160) — v ≈ 34 m/s — a energia cinética máxima a que eles ficam submetidos é a energia cinética do sistema formado pelos três jovens, no ponto de velocidade máxima (B) — Ec=3mV2/2=3x50x1.160/2 — Ec=87.000J=87kJ — R- D
09- Sendo o sistema é conservativo, em todos os casos a velocidade em B é vB, que pode ser calculada pelo Teorema da Energia Mecânica — fazendo AB = h — EmA=EmB — mgh=mVB2/2 — VB=√(2gh) — sendo H a altura do solo até B, o tempo de queda (tq) é obtido pela expressão: H = gtq2/2 — tq=√(2H/g) — na direção horizontal, o movimento é uniforme com velocidade vB — a distância horizontal percorrida durante o tempo de queda é: d = vB tq — d =(√2gh).(√2H/g) — d=2√hH — sendo h e H iguais em todos os casos, a distância de B ao solo também é a mesma para todos eles — R- D
10- Nos dois casos, a deformação da mola é a mesma (x), armazenando as duas molas mesma energia potencial elástica — EPel=kx2/2 — energia potencial gravitacional em relação à linha da
mola não deformada — Epg= = m g x — pela conservação da energia, a velocidade vo de lançamento de um dardo é — Ec=Epel+ Epg — mVo2/2=mgx + kx2/2 — Vo2=2/m(mgx + kx2/2) — Vo=√(mgx + kx2/2) — observe que, como a massa m aparece no denominador, o dardo de maior massa é o que tem menor velocidade inicial, ou seja, o dardo I, que tem um pedaço de chumbo grudado nele.
Após sair dos canos dos brinquedos, desprezando a resistência do ar, os dados ficam sujeitos exclusivamente à força peso, tendo, portanto, a mesma aceleração g — por isso os gráficos são retas paralelas, como mostrado na opção A — R- A
11- Cálculo da energia mecânica em A que é só a energia potencial gravitacional — EmA=mgh=25.10.2,4=600J — energia mecânica em B, só a energia cinética — EmB =mV2/2=25.V2/2=12,5V2 — força de atrito — Fat=μN=μPp=μPcos37o —
Fat=μmgcos37o=0,5x250x0,8 — Fat=100N — sen37o=h/d — 0,6=2,4/d — d=4m — trabalho da força
de atrito — WFat=Fat.d.cos180o=100.4.(-1) — WFat= – 400J — WFat=EmB – EmA — -400=12,5V2 – 600 — V=4m/s — R- D