Transformações de Energia – Exercícios de ENEM
Transformações de Energia – Energia Mecânica
Exercícios com características de ENEM
01-(UFFRJ-RJ)

O salto com vara é, sem dúvida, uma das disciplinas mais exigentes do atletismo. Em um único salto, o atleta executa cerca de 23 movimentos em menos de 2 segundos. Na última Olimpíada de Atenas a atleta russa, Svetlana Feofanova, bateu o recorde feminino, saltando 4,88 m.
A figura a seguir representa um atleta durante um salto com vara, em três instantes distintos.

Assinale a opção que melhor identifica os tipos de energia envolvidos em cada uma das situações I, II, e III, respectivamente.
a) – cinética – cinética e gravitacional – cinética e gravitacional
b) – cinética e elástica – cinética, gravitacional e elástica – cinética e gravitacional
c) – cinética – cinética, gravitacional e elástica – cinética e gravitacional
d) – cinética e elástica – cinética e elástica – gravitacional
e) – cinética e elástica – cinética e gravitacional – gravitacional
02-(UNICAMP-SP)

Um brinquedo que muito agrada às crianças são os lançadores de objetos em uma pista. Considere que a mola da figura a seguir possui uma constante elástica k = 8 000 N/m e massa desprezível.

Inicialmente, a mola está comprimida de 2,0 cm e, ao ser
liberada, empurra um carrinho de massa igual a 0,20 kg. O carrinho abandona a mola quando esta atinge o seu comprimento relaxado, e percorre uma pista que termina em uma rampa. Considere que não há perda de energia mecânica por atrito no movimento do carrinho. A velocidade do carrinho quando ele abandona a mola e a altura da rampa no instante em que o carrinho tem velocidade de 2,0m/s, valem, respectivamente: (considere g=10N/kg)
a) 2,0m/s e 0,3m
b) 6,0m/s e 0,4m
c) 8,0m/s e 0,6m
d) 1,2,0m/s e 1,2m
e) 4,0m/s e 0,6m
03-(FUVEST-SP)

No ”salto com vara”, um atleta corre segurando uma vara e, com perícia e treino, consegue projetar
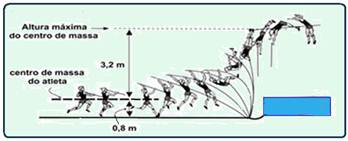
seu corpo por cima de uma barra. Para uma estimativa da altura alcançada nesses saltos, é possível considerar que a vara sirva apenas para converter o movimento horizontal do atleta (corrida) em movimento vertical, sem perdas ou acréscimos de energia. Na análise de um desses saltos, foi obtida a sequência de imagens reproduzida acima.
Nesse caso, é possível estimar que a velocidade máxima atingida pelo atleta, antes do salto, foi de, aproximadamente,
Desconsidere os efeitos do trabalho muscular após o início do salto e considere g=10m/s2.
![]()
04-(UFSM-RS)

Não se percebe a existência do ar num dia sem vento; contudo, isso não significa que ele não existe.
Um corpo com massa de 2kg é abandonado de uma altura de 10m, caindo verticalmente num

referencial fixo no solo. Por efeito da resistência do ar, 4J da energia mecânica do sistema corpo-Terra se transformam em energia interna do ar e do corpo. Considerando o módulo de aceleração da gravidade como g= 10m/s2, o corpo atinge o solo com velocidade de módulo,
em m/s, de
![]()
05-(UNIFESP-SP)

Um dos brinquedos prediletos de crianças no verão é o toboágua. A emoção do brinquedo está associada à grande velocidade atingida durante a descida, uma vez que o atrito pode ser desprezado devido à presença da água em todo o percurso do brinquedo, bem como à existência das curvas fechadas na horizontal, de forma que a criança percorra esses trechos encostada na parede

lateral (vertical) do toboágua.
Sabendo que a criança de 36 kg parte do repouso, de uma altura de 6,0 m acima da base do toboágua, colocado à beira de uma piscina, calcule: Dado: g = 10,0 m/s2
A força normal, na horizontal, exercida sobre a criança pela parede lateral do toboágua, no ponto

indicado na figura (curva do toboágua situada a 2,0 m da sua base) onde o raio de curvatura é igual a 80 cm., vale:
a) 1.200N
b) 2.400N
c) 3.600N
d) 4.800N
e) 6.000N
06-(UFSCAR-SP)

Uma formiga de massa m encontra-se no topo de uma bola de bilhar rigidamente presa ao solo.

A bola possui raio R e superfície altamente polida. Considere g a aceleração da gravidade e despreze os possíveis efeitos dissipativos.
A formiga começa a deslizar na bola com velocidade inicial nula.
O módulo da velocidade da formiga na altura do solo em que ela perde contato com a bola e o valor dessa altura, são, respectivamente:
a) Vx=√(gh) e h=2R/3
b) Vx=√(2gh) e h=R/3
c) Vx=√(g/h) e h=2R
d) Vx=gh e h=R
e) Vx=√(g/2h) e h=2R/3
07-(FGV-RJ)

O gráfico abaixo representa a energia potencial EP, em função do tempo, de uma pequena esfera em movimento oscilatório, presa
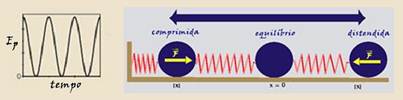
na extremidade de uma mola. Dentre os gráficos I, II, III e IV, aqueles que representam a energia cinética e a energia total do sistema, quando não há efeitos dissipativos, são, respectivamente,

a) I e II.
b) I e III.
c) II e III.
d) II e IV.
e) III e I.
08-(UNESP-SP)

O Skycoaster é uma atração existente em grandes parques de diversão, representado nas figuras a seguir. Considere que em um desses brinquedos, três aventureiros são presos a cabos de aço e içados a grande altura. Os jovens, que se movem juntos no

brinquedo, têm massas iguais a 50 kg cada um. Depois de solto um dos cabos, passam a oscilar tal como um pêndulo simples, atingindo uma altura máxima de 60 metros e chegando a uma altura mínima do chão de apenas 2 metros. Nessas condições e desprezando a ação de forças de resistências, o valor da maior energia cinética, em kJ, a que eles ficam submetidos, é, aproximadamente de:
![]()
09-(UERJ-RJ)

Os esquemas a seguir mostram quatro rampas AB, de mesma altura AC e perfis distintos, fixadas em mesas idênticas, nas quais uma pequena pedra é abandonada, do ponto A, a partir do repouso.

Após deslizar sem atrito pelas rampas I, II, III e IV, a pedra toca o solo, pela primeira vez, a uma distância do ponto B respectivamente igual a dI, dII, dIII e dIV.
A relação entre essas distâncias está indicada na seguinte alternativa:
a) dI > dII = dIII > dIV
b) dIII > dII > dIV > dI
c) dII > dIV = dI > dIII
d) dI = dII = dIII = dIV
10-(UFF-RJ)

Dois brinquedos idênticos, que lançam dardos usando molas, são disparados simultaneamente na vertical para baixo.
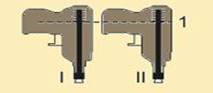
As molas com os respectivos dardos foram inicialmente comprimidas até a posição 1 e, então, liberadas. A única diferença entre os dardos I e II, conforme mostra a figura, é que I tem um pedaço de chumbo grudado nele, o que não existe em II.
Escolha o gráfico que representa as velocidades dos dardos I e II, como função do tempo, a partir do instante em que eles saem dos canos dos brinquedos.

11-(PUC-SP)

Uma criança de massa 25 kg, inicialmente no ponto A, distante 2,4 m do solo, percorre, a partir do repouso, o escorregador esquematizado na figura. O escorregador pode ser considerado um plano inclinado cujo ângulo com a horizontal é de 37°. Supondo o coeficiente de atrito cinético entre a roupa da criança e o escorregador igual a 0,5, a velocidade com que a criança chega à base do escorregador (ponto B) é, em m/s, (g=10m/s2)

Dados: sen 37° = 0,6; cos 37° = 0,8; tg 37° = 0,75
a) 4√3 b) 4√5 c) 16 d) 4 e) 6√3
Confira a resolução comentada
