Trabalho como variação de Energia – EN
Commented Resolution
Work as a variation of Energy
01- Data — E = 94,684,781 MWh ≈ 9.5. 10 7 MWh = 9.5 . 10 13 Wh — L = 0.45. 10 8 J/kg — transforming this amount of energy in joules — E = 9.5. 10 13 Wh = (9.5. 10 13 W).(3.6. 10 3 s) = 3.4. 10 17 J — for oil — E = m L — m = E/L — m = 3.4. 10 17 /0.45 . 10 8 = 7.5. 10 9 kg = 7.5. 10 6 tons — m = 7.5 million tons — R- D
02- The table shows the energy spent in each of the activities, within the time specified in each of the propositions — note that the one that comes closest to the expenditure of 304 kilocalories corresponds to alternative A.
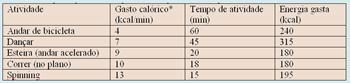
A- A
03- Data — F = 30 N — ∆S = 800 m — the work (W) of a constant force is given by the expression — W F = Fdcosα — the force being parallel to the displacement — α = 0°, cos α = 1 — W F = 30.(800) = 24,000 J = 24 kJ — R- D ![]()
04- Two forces act on the fish — pulling force (which the fisherman applies to lift the fish, vertically and upwards) and the weight of the fish (vertically and downwards) — as the displacement is upwards and the weight of the fish is downwards, they have opposite directions and the work of the weight force is resistant (opposite to the displacement) — A- A
05- a) product density = product mass / product volume — d = 1,000 / (1,312.5 – 62.5) — d = 0.8 g / cm 3
b) total mass of each box – m=10 + 1,000 + 100=1,110g=1.11kg — weight of each box – P=mg=1.11.10 — P=11.1N
W=Ph — W=11.1.1.5 — W=16.65J
06- The work done (energy transferred) to raise the same bucket to the same height at constant speed is the same for Oscarito and Ankito (W=FV=PV), but the minimum force exerted by Oscarito is smaller, since the displacement is greater.
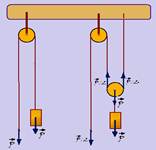
(in this case, the movable pulley doubles the displacement and halves the force) — R- D
07- Force F 1 — W F1 =F 1 .d.cosθ — W F1 =0,4.2,5.cosθ — W F1 =cosθ=k.
Force F 2 — W F2 =F 2 .d.cos2θ — W F2 =0,4.2,5.cos2θ — W F2 =cos2θ — cos2θ =cos2θ – sin2θ — cos2θ=cos(θ + θ ) – sin(θ + θ )=cosθ.cosθ – sinθ.senθ — W F2 =cos 2 θ – sin 2 θ — W F2 = k 2 – (1 – cos 2 θ) — W F2 =cos2θ= k 2 – 1 + k 2 — cos2θ = 2k 2 – 1 — W F2 =cos2θ =2k 2 – 1 — RD
08- Data — m=50g=50.10 -3 =5.10 -2 kg — ∆S=0.5cm=5.10 -1 .10 -2 =5.10 -3 kg — V o =2.10 2 m/s — V=0 — The work done by the kevlar fiber is equal to the work done by the resulting resistive force of the fiber that opposes the bullet, stopping it.
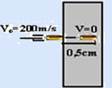
Calculation of work (W) as a variation of kinetic energy — W FR =E cf – E ci =mV 2 /2 – mV o 2 /2 — W FR =0 – 5.10 -2 2.(2.10 2 ) 2 /2 =5.10 -2 .4.10 4 /2=20.10 2 /2 — W FR =1.10 3 J — but, the work of the resulting force also by — W FR =F R .d.cosaα — 10 3 =F.5.10 -3 .cos180 o — 10 3 =F.5.10 -3 .(-1) — F= – 10 3 /5.10 -3 — W FR = – 10.10 2 .10 3 /5 — F= – 2.10 5 N — R- A
09- The variation of potential energy, in the gravitational case, corresponds to the work of the weight force which, being a conservative force, is independent of the trajectory, depending only on the initial and final positions which, in this case, are the same for the three trajectories — only III is correct —
R-C
10- Since the work of the weight force is neglected, you can consider, in the braking process, only the work of the friction force — work of the friction force ( W fat ) = variation of kinetic energy (∆E c ) — W fat = F at .d.cosα=∆E c -E cf – E ci — F at .1.5.10 3 .(-1)= 0 – 4.5.10 4 — F at =30N — R- E
11- d=1g/cm3 = 103 kg /m3 — V=50m3 per second — d=m/V — 103 = m/50 — m=5.104 kg per second — gravitational potential energy stored by m=5.104 kg of water at a height of 160m in 1s, at a place where g=10m/s2 is given by — E p =mgh=5.104 .10.160 — Ep=8.107 J — R- A
12- Calculation to raise the tube using the variation of gravitational potential energy — W=E pi – E f =mgh i – mgh f — W= 0 – 450.10.3.2= – 2.5.10 4 J — R- C
