Resolução Comentada
Óptica Geométrica
Reflexão Total – Dioptro Plano
01- As ondas eletromagnéticas emitidas na região litorânea do Brasil atingem a região amazônica após sofrer reflexão total na ionosfera — R- A
Observação: as ondas de rádio partem da antena emissora e sobem até a parte da atmosfera denominada ionosfera, sofrem reflexão total na mesma, descem e atingem o mar ou a terra, se
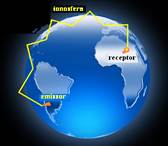
refletem como num espelho, sobem novamente, sofrem nova reflexão total
na ionosfera, retornam com o ciclo se repetindo até atingirem uma ou mais antenas receptoras que, se estiverem na mesma frequência das ondas irradiadas pela antena emissora, recebem o som por ela emitidos — se nos pontos onde as ondas atingem o mar ou a terra tivesse antenas receptoras (rádio) ele também receberia os sinais emitidos (desde que as ondas irradiadas pelo emissor fossem da mesma frequência que as recebidas pelo receptor).
02- senL=nmenor/nmaior — senL=1/2 — L=30o — sofrerá refração se incidir com ângulo inferior ao ângulo limite (30o).
R- C
Observação: Se você não domina a teoria leia atentamente as informações a seguir — condições para que ocorra reflexão total — considere um raio de luz se refratando de um meio mais refringente (maior índice de refração), por exemplo, água, para outro meio menos refringente (menor índice de refração), por exemplo, ar — observe na sequência de figuras que, à medida que o ângulo que o raio incidente (na água) vai aumentando, o ângulo do raio
refratado (no ar) aumenta em proporção maior — isso ocorre até que, quando a luz incide na superfície da água com ângulo r’’ (figura 3), ela se refrata no ar praticamente paralelo à superfície da água (emergência rasante) — nesse caso específico, denominamos r’’ de ângulo limite L.
A partir daí começa o que se denomina de reflexão total.
Para qualquer ângulo de incidência maior que o ângulo limite L ( i > L), o raio de luz sofre reflexão total ou reflexão interna retornando à água tal que i=r.
Considere dois meios homogêneos e transparentes A e B, tal que nA>nB e com a luz se refratando de A para B.
Aplicando a lei de Snell-Descartes na figura acima — nA.senL = nB.sen90o — nA.senL = nB.1 —
1a – A luz deve se propagar do meio mais refringente (maior índice) para o meio menos refringente (menor índice)
2a – A luz deve incidir com ângulo sempre maior que o ângulo limite L.
03- Para que o raio de luz sofra reflexão total ele deve incidir do meio mais refringente (maior índice de refração) para o meio menos refringente (menor índice de refração) e deve incidir com ângulo menor que 90o, pois se fosse maior que 90o, ele passaria a incidir pelo outro meio — R- D
Fibras ópticas — usadas como meio de transmissão de ondas eletromagnéticas (como a luz). Feitas de plástico ou de vidro e tem diâmetros variáveis (mais finos que um fio de cabelo até vários milímetros). Em relação aos cabos metálicos de cobre tem a vantagem de serem imunes às interferências eletromagnéticas além de não serem afetados com problemas decorrentes da eletricidade.
A luz se propaga no interior do núcleo num caminho totalmente espelhado devido ao fenômeno da reflexão total que ocorrerá no interior do núcleo desde que o índice de refração do núcleo (nn) seja maior que o índice de refração da casca (nc) e que o ângulo de incidência em relação à normal ao incidir na casca seja maior que o ângulo limite L.
Utilizados em comunicações (rede telefônica, televisão por cabo, distribuição de energia elétrica), em medicina (sistemas de monitoração interna do corpo humano e instrumentação cirúrgica), etc. — não importa a distância, levam a informação quase instantaneamente, ou seja, à velocidade próxima à da luz.
04- R- B — Miragens – Devido à variação da densidade do ar com a temperatura, temos a ilusão em dias quentes e secos, de poças de água, imagens de carros, de nuvens, etc., de miragens em desertos , pois o Sol em contato com o solo deixa o ar mais quente e consequentemente menos refringente que o ar das camadas superiores. Isso faz com que os raios de luz sofram reflexão total
em camadas próximas ao solo,, subam e atinjam os olhos de um observador, que terá a impressão de que no solo existe um espelho fornecendo a imagem do objeto. O fenômeno também pode acontecer embora menos frequentemente, nos mares.
05- I) Correta — como a atmosfera é transparente, mas não homogênea, os raios solares sofrem desvio ao atravessá-la, fazendo com que o pôr do sol seja uma miragem — como, na refração, as radiações de menor frequência (vermelha, amarela e alaranjada) sofrem menor desvio, o observador vê a imagem do Sol com predominância dessas cores, daí, aquele tom roseado — como mostra a figura ilustra (de maneira exagerada).
(II) Falsa — o ar é menos refringente que a água — ao passar do meio menos para o mais refringente, a luz aproxima da normal, não ocorrendo reflexão total — esse fenômeno só ocorre quando o sentido de propagação da luz é do meio mais para o menos refringente, quando o ângulo de incidência é maior que o ângulo limite.
(III) Falsa — na refração não há alteração da frequência que é a característica da onda (cor) — cada
cor tem a mesma frequência independente do meio onde esteja se propagando.
R- D
06- Observe a figura abaixo — o asfalto se aquece, aquecendo as camadas de ar próximas a ele — quanto mais baixa a camada, maior a sua temperatura — assim, a temperatura do ar diminui com a altura da camada — o ar quente sobe, fazendo com que as camadas mais baixas se tornem mais rarefeitas provocando um aumento da densidade com a altura da camada — consequentemente, o índice de refração também sofre um aumento, sendo as camadas inferiores menos refringentes — a passagem de um raio de uma camada (+) refringente para outra (–) refringente faz com que o raio se afaste da normal na trajetória descendente, fazendo aumentar o ângulo de refração, até atingir o ângulo limite e a reflexão total, acontecendo o inversão na trajetória ascendente.
R- C
07- Estude com atenção a teoria abaixo e, em seguida aplique-a ao exercício:
Na figura I o ponto objeto real P está dentro da água e emitindo dois raios de luz, um vertical que não sofre desvio e o outro oblíquo que, ao se refratar para o ar, afasta-se da normal atingindo os olhos do observador e determina a imagem virtual (P’), acima do objeto real P.
Na figura II o ponto objeto real P está no ar e emitindo dois raios de luz, um vertical que não sofre desvio e o outro oblíquo que, ao refratar-se para a água, aproxima-se da normal atingindo os olhos do observador e determina a imagem virtual P’, acima do objeto real P.
Observe que, em qualquer das duas situações a imagem está sempre acima do objeto.
Aplicando a lei de Snell-Descartes, em ambos os casos, temos:
N1.seni=n2. senr (I) — considerando os ângulos muito pequenos de modo que o observador esteja bem próximo da normal —≈ seni ≈ tgi≈ a/do (II) e senr ≈ tgr ≈ a/di (III) — substituindo II e III em I — n1.do=n2. Di
Adaptando a equação de acordo com a figura abaixo:
Onde:
di—- distância vertical da imagem à superfície de separação (interface) água-ar (distância aparente, em que o observador enxerga a imagem)
do—- distância vertical do objeto, até a superfície de separação (interface) água-ar.
no—- índice de refração do meio onde está o observador (no caso, ar)
ni—- índice de refração do meio onde está o objeto a imagem (no caso, água)
Resolução do exercício: Observe a figura abaixo e veja que a imagem está sempre acima do objeto e na mesma reta vertical:
do=10m — di=? — no=1,3 — ni=1 — di.ni=do.no — di.1=10.1,3 — di=13m — R- C
08- Continuará vendo os 12 azulejos, mas mais curtos, de altura (lado vertical) menor e valendo
di.ni==do.no — do=12.12 — do=144cm — no=1 — ni=4/3 — di.ni==do.no — di.3/3=144.1 — di=108cm/12=9cm — R- A
Observação: Imagem e objeto no ar e na água tem sempre as mesmas dimensões. A água não aumenta o tamanho de um objeto mergulhado nela, mas como aproxima-o de quem está olhando, dando a impressão de que está mais curto verticalmente.
Observe na figura acima que a refração diminui as dimensões verticais, mas não as horizontais, fazendo o azulejo parecer mais curto. Então, se a piscina tiver 10 azulejos você continuará vendo os 10, mas mais curtos (de lado vertical menor).
Assim, um espelho esférico ou uma lente, no ar ou na água, mantém sua distancia focal e seu centro de curvatura, que são retas e nesses meios seu comprimento é o mesmo.
Observe na figura acima que a refração diminui as dimensões verticais, mas não as horizontais, fazendo o azulejo parecer mais curto. Então, se a piscina tiver 10 azulejos você continuará vendo os 10, mas mais curtos (de lado vertical menor).
Assim, um espelho esférico ou uma lente, no ar ou na água, mantém sua distancia focal e seu centro de curvatura, que são retas e nesses meios seu comprimento é o mesmo.
09- Leia a teoria a seguir: Um gato que observa um peixe dentro de um aquário enxerga-o mais
próximo da parede do aquário (observador no ar). Ao mesmo tempo, o peixe observa o gato mais distante do aquário (observador na água) — isso ocorre porque a luz ao passar de um meio mais refringente (água) para outro meio menos refringente (ar), ele se afasta da normal e, em caminho inverso ele se aproxima da normal — R- A
10- A resposta deve estar entre as alternativas A, D ou C, pois D1 capta a luz emitida na vertical
onde não sofre desvio (incidência normal), assim o indicador só pode estar na vertical. Quando se refrata da lâmina de tecido biológico (água) para o ar a luz sofre desvio, se aproximando da normal, até atingir D2. A única alternativa que satisfaz é a C — R- C
11- Veja a figura abaixo:
Se o raio de luz sofrer reflexão e refração em ambas as faces e, nelas, retornar ao ar, os seguintes
ângulos serão iguais —a=b=g=h — c=d=e=f — observe que os raios incidente e emergente são paralelos.
R- A
12- Como a imagem está acima do observador, ela estará mais próxima do mesmo e, devido ao campo visual maior dará ao observador a impressão de ser maior que o objeto — R- B
13- Nar=1 — nvidro = √3 — e = √3 cm — como o ângulo entre o raio e a lâmina é de 30°, o ângulo de incidência é: i = 60° — o raio provem do ar, atravessa a lâmina e volta para o ar, o raio emergente é paralelo ao incidente — i’ = i = 60° — observe a
figura — lei de Snell na primeira face — nar sen i = nvidro sen r — (1) sen 60° = √3 sen r — √3/2 = √3sen r — sem r = 1/2 — r = 30o — no ponto C — os ângulos BCA e r são alternos-internos — BCA= 30° — os ângulos BCD e i’ são opostos pelo vértice — BCD= 60° — BCD=BCA + ACD — 60° = 30° + ACD— ACD= 30° — no triângulo ABC — cos 30o=BC/AC — √3/2 = √3/AC — AC=2cm — no triângulo ACD — sen30o=AD/AC — 1/2=x/2 — x=1cm — R- B