Geometric Optics – Total Reflection – Flat Diopter – Resolution – EN
Commented Resolution
Geometric Optics
Total Reflection – Flat Diopter
01- Electromagnetic waves emitted in the coastal region of Brazil reach the Amazon region after undergoing total reflection in the ionosphere — A- A
Note: radio waves leave the transmitting antenna and rise to the part of the atmosphere called the ionosphere, undergo total reflection in it, descend and reach the sea or land, if
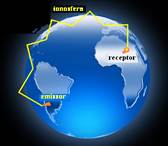
reflect as in a mirror, rise again, undergo new total reflection
in the ionosphere, they return with the cycle repeating until they reach one or more receiving antennas which, if they are at the same frequency as the waves radiated by the transmitting antenna, receive the sound emitted by it — if at the points where the waves reach the sea or land there were receiving antennas (radio) it would also receive the signals emitted (as long as the waves radiated by the transmitter were of the same frequency as those received by the receiver).
02- senL=n smaller /n larger — senL=1/2 — L=30 o — will undergo refraction if it hits at an angle smaller than the limiting angle (30 o ).
R-C
Note : If you do not master the theory, read the following information carefully — conditions for total reflection to occur — consider a ray of light refracting from a more refractive medium (higher refractive index), for example, water, to another less refractive medium (lower refractive index), for example, air — note in the sequence of figures that, as the angle at which the incident ray (in the water) increases, the angle of the ray
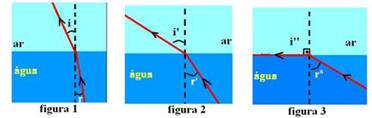
refracted (in the air) increases in a greater proportion – this occurs until, when the light hits the surface of the water at an angle r” (figure 3), it refracts in the air practically parallel to the surface of the water (grazing emergence) – in this specific case, we call r” the limiting angle L.
From there begins what is called total reflection .
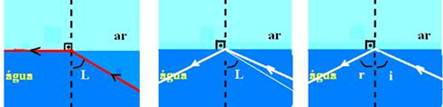
For any angle of incidence greater than the limiting angle L (i > L), the light ray undergoes total reflection or internal reflection returning to the water such that i = r.
![]() Calculation of the limit angle.
Calculation of the limit angle.
Consider two homogeneous and transparent media A and B, such that n A >n B and with light refracting from A to B.
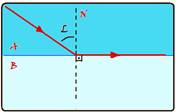
Applying the Snell-Descartes law in the figure above — n A .senL = n B .sen90 o — n A .senL = n B .1 —
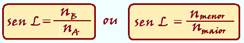
![]() Conditions for total reflection to occur:
Conditions for total reflection to occur:
1 a – Light must propagate from the most refractive medium (highest index) to the least refractive medium (lowest index)
2 a – The light must always fall at an angle greater than the limit angle L.
03- For the light ray to undergo total reflection, it must fall from the most refractive medium (highest refractive index) to the least refractive medium (lowest refractive index) and must fall at an angle less than 90 ° , because if it were greater than 90 ° , it would fall through the other medium — R- D
Optical fibers — used as a means of transmitting electromagnetic waves (such as light). Made of plastic or glass and have variable diameters (from thinner than a strand of hair to several millimeters). Compared to copper metal cables, they have the advantage of being immune to electromagnetic interference and are not affected by problems arising from electricity.

Light propagates inside the core in a completely mirrored path due to the phenomenon of total reflection that will occur inside the core as long as the refractive index of the core (n n ) is greater than the refractive index of the cladding (n c ) and the angle of incidence in relation to the normal when incident on the cladding is greater than the limiting angle L.
Used in communications (telephone network, cable television, electricity distribution), in medicine (internal monitoring systems of the human body and surgical instrumentation), etc. — regardless of the distance, they carry information almost instantly, that is, at a speed close to that of light.
04- R- B — Mirages – Due to the variation in air density with temperature, on hot and dry days we have the illusion of puddles of water, images of cars, clouds, etc., of mirages in deserts, because the Sun in contact with the ground makes the air hotter and consequently less refractive than the air in the upper layers. This causes the light rays to undergo total reflection.
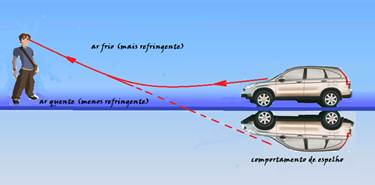
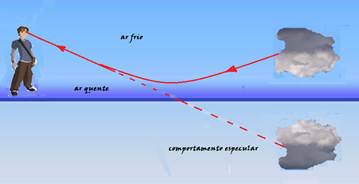
in layers close to the ground, rise and reach the eyes of an observer, who will have the impression that there is a mirror on the ground providing the image of the object. The phenomenon can also occur, although less frequently, in the seas.
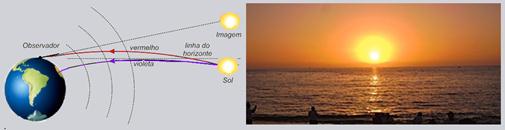
05- I) Correct — as the atmosphere is transparent, but not homogeneous, the sun’s rays are deflected when passing through it, making the sunset a mirage — as, in refraction, the lower frequency radiations (red, yellow and orange) are less deflected, the observer sees the image of the Sun with a predominance of these colors, hence, that pinkish tone — as shown in the figure (in an exaggerated manner).
(II) False — air is less refractive than water — when passing from the less refractive medium to the more refractive medium, the light approaches the normal, with no total reflection occurring — this phenomenon only occurs when the direction of propagation of the light is from the more refractive medium to the less refractive medium, when the angle of incidence is greater than the limiting angle.
(III) False — in refraction there is no change in frequency which is the characteristic of the wave (color) — each

color has the same frequency regardless of the medium in which it is propagating.
R-D
06- Observe the figure below — the asphalt heats up, heating the layers of air close to it — the lower the layer, the higher its temperature — thus, the air temperature decreases with the height of the layer — the hot air rises, causing the lower layers to become more rarefied, causing an increase in density with the height of the layer — consequently, the refractive index also increases, with the lower layers being less refractive — the passage of a ray from a (+) refractive layer to another (–) refractive layer causes the ray to move away from the normal on the downward trajectory, increasing the angle of refraction, until it reaches the limit angle and total reflection, with the inversion occurring on the upward trajectory. 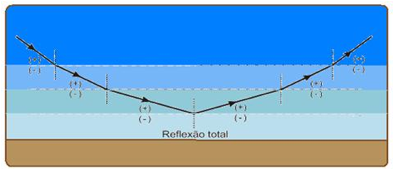
R-C
07- Study the theory below carefully and then apply it to the exercise:
In figure I, the real object point P is inside the water and emitting two rays of light, one vertical that does not undergo deviation and the other oblique that, when refracted into the air, moves away from the normal, reaching the observer’s eyes and determining the virtual image (P’), above the real object P.
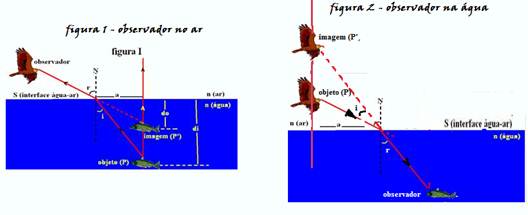
In figure II, the real object point P is in the air and emitting two rays of light, one vertical that does not undergo deviation and the other oblique that, when refracted towards the water, approaches the normal, reaching the observer’s eyes and determining the virtual image P’, above the real object P.
Note that in either situation the image is always above the object.
![]() Deduction of the plane diopter equation
Deduction of the plane diopter equation
Applying the Snell-Descartes law, in both cases, we have:
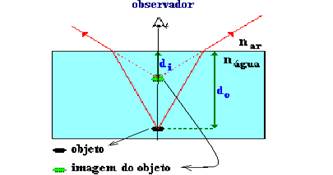
N 1 . seni=n 2 . senr (I) — considering the angles very small so that the observer is very close to the normal —≈ seni ≈ tgi≈ a/d o (II) and senr ≈ tgr ≈ a/d i (III) — substituting II and III in I — n 1 .d o =n 2 . D i
Adapting the equation according to the figure below:
![]()
Where:
di—- vertical distance from the image to the water-air separation surface (interface) (apparent distance, at which the observer sees the image)
do—- vertical distance from the object to the water-air separation surface (interface).
no—- refractive index of the medium where the observer is (in this case, air)
ni—- refractive index of the medium where the object and image are located (in this case, water)
Exercise resolution: Observe the figure below and see that the image is always above the object and on the same vertical line:
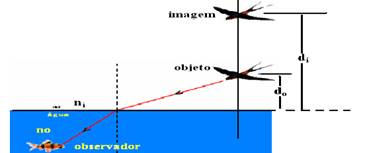
do=10m — di=? — no=1,3 — ni=1 — di.ni=do.no — di.1=10.1,3 — di=13m — R- C
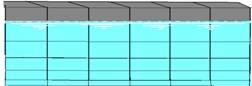
08- You will continue to see the 12 tiles, but shorter, with a lower height (vertical side) and worth
d i .n i ==d o .n o — d o =12.12 — d o =144cm — n o =1 — n i =4/3 — d i .n i ==d o .n o — di. 3/3=144.1 — d i =108cm/12=9cm — R- A
Note: Images and objects in air and water always have the same dimensions. Water does not increase the size of an object immersed in it, but rather brings it closer to the viewer, giving the impression that it is shorter vertically.
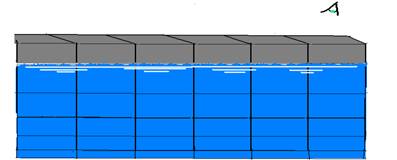
Note in the figure above that refraction reduces the vertical dimensions, but not the horizontal ones, making the tile appear shorter. So, if the pool has 10 tiles, you will still see all 10, but shorter (with a shorter vertical side).
Thus, a spherical mirror or a lens, in air or water, maintains its focal distance and its center of curvature, which are straight lines and in these media its length is the same.
Note in the figure above that refraction reduces the vertical dimensions, but not the horizontal ones, making the tile appear shorter. So, if the pool has 10 tiles, you will still see all 10, but shorter (with a shorter vertical side).
Thus, a spherical mirror or a lens, in air or water, maintains its focal distance and its center of curvature, which are straight lines and in these media its length is the same.
09- Read the following theory: A cat that observes a fish inside an aquarium sees it more clearly.
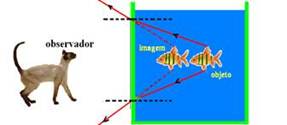
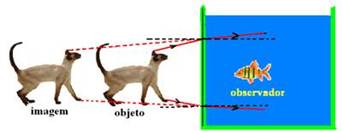
close to the aquarium wall (observer in the air). At the same time, the fish observes the cat further away from the aquarium (observer in the water) — this occurs because when light passes from a more refractive medium (water) to a less refractive medium (air), it moves away from the normal and, in the opposite direction, it approaches the normal — R- A
10- The answer must be among alternatives A, D or C, since D 1 captures the light emitted vertically
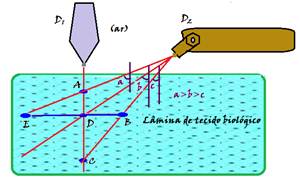
where it does not undergo deviation (normal incidence), so the indicator can only be vertical. When it refracts from the biological tissue slide (water) to the air, the light undergoes deviation, approaching the normal, until it reaches D 2 . The only satisfactory alternative is C — R- C
11- See the figure below:
If the light ray undergoes reflection and refraction on both faces and, from them, returns to the air, the following
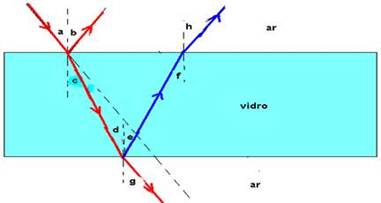
angles will be equal —a=b=g=h — c=d=e=f — note that the incident and emerging rays are parallel.
A- A
12- As the image is above the observer, it will be closer to him and, due to the larger visual field, it will give the observer the impression of being larger than the object — R- B
13- N air = 1 — n glass = √3 — e = √3 cm — as the angle between the ray and the blade is 30°, the angle of incidence is: i = 60° — the ray comes from the air, passes through the blade and returns to the air, the emerging ray is parallel to the incident one — i’ = i = 60° — observe the
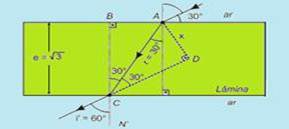
figure — Snell’s law on the first face — n ar sin i = n glass sin r — (1) sin 60° = √3 sin r — √3/2 = √3sin r — without r = 1/2 — r = 30 o — at point C — angles BCA and r are alternate interior — BCA= 30° — angles BCD and i’ are opposite by the vertex — BCD= 60° — BCD=BCA + ACD — 60° = 30° + ACD— ACD= 30° — in triangle ABC — cos 30 o =BC/AC — √3/2 = √3/AC — AC=2cm — in triangle ACD — sin 30 o =AD/AC — 1/2=x/2 — x=1cm — R- B
