Resolução Comentada – Óptica Geométrica – Espelhos Esféricos
Resolução Comentada
Óptica Geométrica
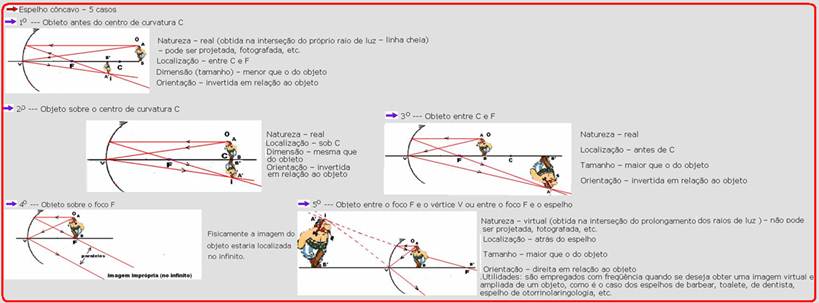
Espelhos Esféricos
01- Características de um espelho convexo — Para qualquer localização do objeto, a imagem terá sempre:
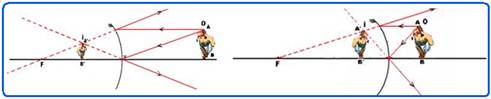
Natureza – virtual
Localização – atrás do espelho e entre V e F e observe que à medida que o objeto se aproxima do espelho, a imagem também se aproxima e aumenta de tamanho, mas está sempre entre V e F..
Tamanho – menor que o do objeto
Orientação – direita em relação ao objeto
Utilidades: Os espelhos convexos são empregados como retrovisores em veículos, cabines de segurança, elevadores, etc. Sua vantagem sobre o espelho plano, nesse particular, é ter maior campo visual. Têm, entretanto, o inconveniente de não darem noção da distância.
Nossos olhos estão acostumados com imagens em espelhos planos, onde imagens de objetos mais distantes nos parecem cada vez menores — esse condicionamento é levado para o espelho convexo — o fato de a imagem ser menor que o objeto é interpretado pelo cérebro como se o objeto estivesse mais distante do que realmente está — essa falsa impressão é desfeita quando o motorista está, por exemplo, dando marcha a ré em uma garagem, vendo apenas a imagem dessa parede pelo espelho convexo — ele para o carro quando percebe pela imagem do espelho convexo que está quase batendo na parede — ao olhar para trás, por visão direta, ele percebe que não estava tão próximo assim da parede —– R- C
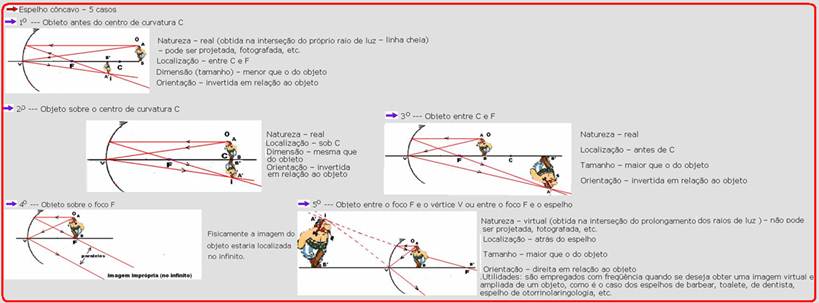
02- R- A — estude atentamente a tabela abaixo e observe que se trata do 5o caso.
03- Num espelho esférico côncavo gaussiano a distância focal (f) é metade do raio de curvatura (R),
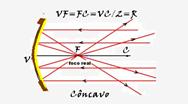
que, por sua vez, é metade do diâmetro (d) — f=R/2=(d/2)/2 — f=d/4 — d=4f — R- D
04- Observe na figura fornecida, que a imagem do objeto real está invertida e ampliada — esse caso só acontece para um espelho esférico côncavo, quando o objeto está entre o centro de curvatura (C) e o foco (F) — observe na tabela abaixo — é o terceiro caso —
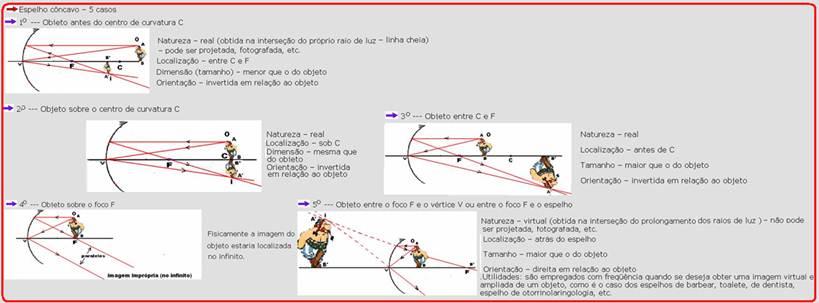
R- D
05- Para que os raios retornem paralelos a lâmpada L deve estar no foco de E’ (todo raio de luz que incide passando pelo foco retorna paralelamente ao eixo principal) e no centro de curvatura de E’’ (
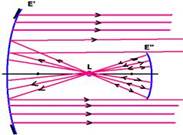
todo raio de luz que incide passando pelo centro de curvatura retorna sobre ele mesmo) — assim, todo raio de luz que emerge à esquerda de L e incide sobre E’’ retorna sobre si mesmo, passa pelo foco de E’ e retorna novamente de forma paralela — R- E
06- Só imagem virtual não pode ser projetada o que, nos espelhos côncavos, só acontece quando o objeto estiver a uma distância inferior à distancia focal f (40cm) — trata-se do caso no 5 da tabela abaixo:
R- A
07- Observe na figura abaixo que P’ está exatamente abaixo de P e com o mesmo tamanho (sob e
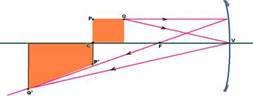
sobre C) e usando os dois raios notáveis foi localizado Q’ — R- D
08- O objeto (lâmpada) está sob a caixa e sobre o foco do espelho e nessas condições a imagem será real, do mesmo tamanho que o objeto e estará sobre ele (segundo caso da tabela abaixo):
— como objeto e imagem são idênticos e terão o mesmo brilho (mesma potência de 40W) — R- A
09- Situação inicial (t=0) — distância do objeto ao espelho – P=50cm — distância focal do espelho – f=10cm — equação dos pontos conjugados – 1/f=1/P+1/P’ — 1/10=1/50+1/P’ — 1/10 – 1/50=1/P’ — 4/50=1/P’ — P’=12,5cm (posição inicial da imagem – distância inicial da imagem ao espelho) — situação final (t=5s) — V=ΔS/Δt — 4= ΔS/5 — ΔS=20cm — como ele se aproxima do espelho sua nova distância do vértice do espelho será — P=50 – 20 — P=30cm — f=10cm — 1/10 = 1/30 + 1/P’ — P’= 15cm (nova posição da imagem distância final da imagem ao espelho) — A imagem percorreu ΔS=15 – 12,5 — ΔS=2,5cm — R- E
10- Espelho convexo — f=-10cm — P=6cm — 1/-10=1/6 + 1/P’ — P’= -3,75cm (distância da imagem ao vértice do espelho) — i/O=-P’/P — 1,5/O=-(-3,75)/6 — O=2,4cm (altura do objeto) — veja a figura I — espelho côncavo — f=10cm
— i=-1,5cm (imagem invertida) — O=2,4cm — i/O=-P’/P — -1,5/2,4=-P’/P — P’=0,625P — 1/10=1/P + 1/0,625P — P=16,25/0,625 — P=26cm —(veja figura II) — R- C
11- O espelho só pode ser côncavo, pois a imagem é direita (virtual) e maior — distância da pessoa ao espelho — p = 10 cm — aumento linear transversal (positivo porque a imagem é direita) — A = 5 — A= – P’/P — 5= – P’/10 — P’=-50cm ( a imagem é virtual P’<0 e está 50cm atrás do espelho) — equação dos pontos conjugados — 1/f=1/P + 1/P’ — 1/f=1/10 + 1/(-50) — 1/f=(5 – 1)/50 — f=50/4 — f=12,5cm — R- A