(MUV) Uniformly Varied Motion – EN
(MUV) UNIFORMLY VARIED MOTION
Uniformly Varied Motion (MUV)
01-(ENEM-MEC)

In a 100m race, the typical performance of a standard runner is represented by the following graph:
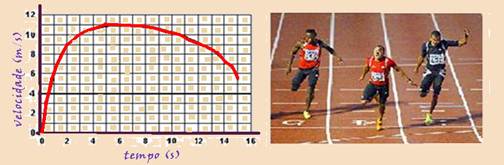
In what time interval does the runner show maximum acceleration?
a) Between 0 and 1 second.
b) Between 1 and 5 seconds.
c) Between 5 and 8 seconds.
d) Between 8 and 11 seconds.
e) Between 9 and 15 seconds.
02–(ENEM-MEC)

Superman and the laws of motion
One reason to think about the physics of superheroes is, above all, that it is a fun way to explore many interesting physical phenomena, from everyday phenomena to events considered fantastic. The following figure shows Superman launching himself into space to reach the top of a building of height H. It would be possible to assume that with his superpowers he would be flying under his own power, but consider that he made a great leap.

In this case, his final velocity at the highest point of the jump must be zero, otherwise he would continue to rise. Since g is the acceleration of gravity, the relationship between Superman’s initial velocity and the height reached is given by: v2 = 2gh.
The height Superman reaches in his jump depends on the square of his initial velocity because
(A) the height of his jump is proportional to his average speed multiplied by the time he remains in the air squared.
(B) the time it remains in the air is directly proportional to the acceleration of gravity and this is directly proportional to the speed.
(C) the time it remains in the air is inversely proportional to the acceleration of gravity and this is inversely proportional to the average speed.
(D) the acceleration of the movement must be squared, as there are two accelerations involved: the acceleration of gravity and the acceleration of the jump.
(E) the height of the jump is proportional to its average speed multiplied by the time it remains in the air, and this time also depends on its initial speed.
Exercises with ENEM characteristics
03- (UNCISAL-AL)

João Gabriel, a UNCISAL entrance exam candidate, is preparing for the university entrance exams and is going to visit the exam location. He leaves his house by car and, starting from his rest, drives along a straight avenue that takes him directly to the desired location. The avenue has intersections with traffic lights and imposes a speed limit, which João Gabriel obeys. The graph that best describes the behavior of his car’s speed as a function of time, from the time he leaves his house until he arrives at the exam location, where he parks at time t’, is:
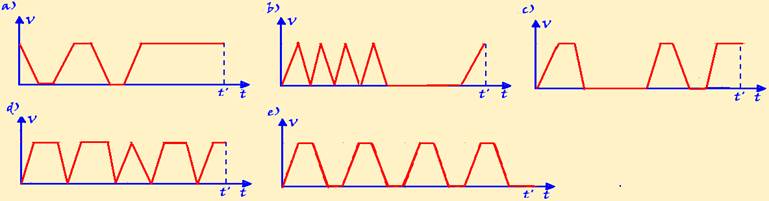
04-(PUC-MG)

AT THE TIME OF THE ACCIDENT, BRAZILIAN SLOWED DOWN
It was the final moments of the second block of qualifying for the Hungarian GP. Felipe Massa had the third best time, but decided to set a fast lap, trying to improve, looking for the ideal setup for Q3, the decisive part of the session, the fight for pole position. He was driving along the short straight between turns 3 and 4 of the Hungaroring track and was starting to slow down from almost 360 km/h.

to 270 km/h when it went out. With his feet firmly on both the brake and the accelerator, he did not turn the steering wheel to the left, passed through a strip of grass, returned to the track and went through the escape area until he hit the tire barrier head-on.
The racetrack watched the scenes in astonishment, unable to understand the driver’s lack of reaction. The mystery was only solved by the images from the onboard camera: a piece hit the left side of the helmet, causing the Ferrari driver to lose his reflexes.
As stated in the text and considering the approximations made, mark the option whose graph best represents the speed of Felipe Massa’s vehicle as a function of time.

05-(CEFET-CE)

Below is a table to compare the acceleration of some vehicles. In all cases, the test was carried out with the vehicles accelerating from 0 to 100 km/h. Note the time required for all vehicles to reach the same speed variation:
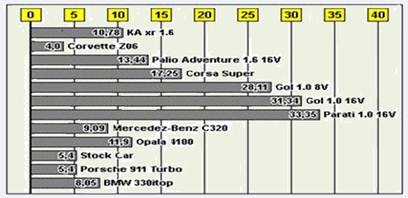
Taking the graph presented as a reference, mark the alternative that correctly indicates the vehicle with the greatest acceleration and indicate the approximate relationship between its acceleration and that of the vehicle with the lowest acceleration.
a) Parati is 8 times bigger
b) Parati is 8 times smaller
c) Corvette is 8 times bigger
d) Corvette is 8 times smaller
e) Corvette is 10 times bigger
06-(PUC-PR)

A car travels on a straight road. At time t = 0 s, the brakes are applied, causing a constant acceleration until the speed is zero, as shown in the figure.
The table shows the speed at certain times

Based on this information, some statements are made about the movement:
I. The car presents an acceleration in the direction of travel.
II. The displacement of the vehicle in the first 2 s is 34 m.
III. The acceleration of the vehicle is -1.5 m/s 2 .
IV. Speed varies inversely proportionally to elapsed time.
V. The vehicle’s speed is zero at 7.5 s.
The following is correct:
![]()
07-(UFPR-PR)

In an international cycling race, two of the cyclists, a Frenchman and, separated by a distance of 15 m in front of him, an Englishman, move at equal and constant speeds of module 22 m/s.

Now consider that the representative
The Brazilian cyclist in the race, when overtaking the French cyclist, has a constant speed of 24 m/s and begins a constant acceleration of 0.4 m/s2, with the objective of overtaking the English cyclist and winning the race. At the moment he overtakes the French cyclist, there are still 200 m to go to the finish line. Based on this data and assuming that the English cyclist, when overtaken by the Brazilian, maintains the characteristics of his movement constant, indicate the correct alternative for the time spent by the Brazilian cyclist to overtake the English cyclist and win the race.
![]()
08-(UFES-ES)

A predator, starting from rest, reaches its maximum speed of 54 km/h in 4 s and maintains that speed for 10 s. If it does not reach its prey in those 14 s, the predator gives up the hunt. The prey, starting from rest, reaches its maximum speed, which is 4/5 of the predator’s maximum speed, in 5 s and can maintain it for longer than the predator.

Assume that the accelerations are constant, that the start of the attack and the start of the flight are simultaneous and that the predator and prey start from rest. For the predator to be successful in its hunt, the maximum initial distance between it and the prey is:
![]()
