Resolução Comentada – Movimento Uniformemente Variado (MUV)

Resolução Comentada 

Movimento Uniformemente Variado (MUV)

01- Quanto mais inclinada reta representativa da velocidade maior será a aceleração, pois a=∆V/∆t,ou seja, quanto maior ∆V e menor ∆t, maior será a aceleração a  —  R- A

02- Trata-se da equação de Torricelli, V² = V_o² + 2.a.h  — com V=0  —  cuja dedução é feita a partir de Vm = ΔS/Δt  —  onde   —  Vm = (V + V0)/2=h/t  —  h=(V + Vo)t/2  —  h = Vm.t/2  —  observe nessa equação que h é proporcional a Vm e at  —  R- E

03-  Observe atentamente que o único gráfico coerente com o enunciado é o da alternativa E  —  em cada trecho, ele acelera, mantém velocidade constante, freia e para e assim por diante  —  R- E

04- Observe no enunciado que ele começou a reduzir a velocidade de 360kmh para 270kmh quando apagou  —  movimento retardado com velocidade diminuindo  —  R- C

05- Menor tempo – maior aceleração – Corvette  —   a_m=100/4=25(km/h)/s  —  maior tempo – menor aceleração – Parati  —-  a_m=100/33,35=3(km/h)/s  —  R- C

06- I – Falsa – é no sentido contrário ao do movimento – a velocidade está diminuindo

II –

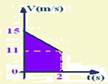
ΔS=(15 + 11).2/2=26m  —  Falsa

III – a=(9 – 15)/3=-2m/s²  —  Falsa

IV – Correta – observe que à medida que a velocidade diminui o tempo aumenta

V – V= V_o + at  —  0=15 – 2t  —  t=7,5s  —  Correta

R- D

07-  Observe a figura abaixo que ilustra a situação descrita no instante t = 0  —  o ciclista inglês (I)

executa movimento uniforme e o ciclista brasileiro (B) executa movimento uniformemente variado  —  a partir do instante mostrado (t = 0), as respectivas funções horárias dos espaços são  —  SI = 15 + 22 t  e  SB = 24 t  + 0,4.t²/2  —  no encontro, essas equações são igualadas  —   

24 t + 0,2 t²  = 15 + 22 t  —   0,2 t² + 2 t – 15 = 0  —  Resolvendo essa equação do 2º grau  —  t₁ = -15 s  e  t₂ = 5 s  —   t = 5 s  —  o ciclista brasileiro alcança o ciclista inglês no instante t = 5 s  —  R- E

08- Cálculo da distância percorrida pelo predador  —  entre 0 e 4s  —  acelerado com a=(54/3,6 – 0)/(4 – 0)=3,75m/s²  —  ΔS₁=V_ot + at²/2=0.4 +3,75.16/2  —  ΔS₁=90m  —  entre 4s e 10s é um MU com V=15ms  —  V= ΔS/Δt  —  15= ΔS₂/6  —  ΔS₂=90m  — ΔS_predador=90 + 90  —  ΔS_predador=180m

Cálculo da distância percorrida pela presa  —  entre 0 e 5s  —  acelerado com a=(12 – 0)/(5 – 0)=2,4m/s²  —  ΔS₁=V_ot + at²/2=0.5 +2,4.25/2  —  ΔS₁=30m  —  entre 5s e 10=14s é um MU com V=12ms  —  V= ΔS/Δt  —  12= ΔS₂/9  —  ΔS₂=108m  —  ΔS_predador=30 + 108  —  ΔS_presa=138m

Resposta  —  ΔS=180 – 138  —  ΔS=42m  —  R- C

 

Voltar para os exercícios