Movimento Circular – Resolução
Resolução Comentada
Movimento Circular (MC)
01- I- Correta — 2 coroas dianteiras x 5 coroas traseiras=10 marchas

II- Falsa — elas estão ligadas por uma corrente cuja velocidade é a mesma que as velocidades da coroa (no pedal) e da catraca (na roda) — quanto maior a coroa (no pedal) e menor a catraca (na roda), a corrente se move com velocidade maior fazendo a
roda efetuar mais voltas, a bicicleta anda mais depressa e você efetua mais força no pedal.
III- Correta — quanto menor a coroa (no pedal) e maior a catraca (na roda), a corrente se move com velocidade menor fazendo a roda efetuar menos voltas, a bicicleta anda mais devagar e você efetua menos força no pedal.
R- A
02- A velocidade tangencial de qualquer ponto da periferia da engrenagem da roda é a mesma que a de qualquer ponto da periferia da engrenagem dos pedais que por sua vez ´a mesma que de qualquer ponto da corrente — Vepedais=Veroda — 2πRepedais.fepedais=2πReroda.feroda — (30/2).1=(10/2).feroda — feroda=3 voltas — ao efetuar uma volta completa a roda de raio 80cm percorre — ∆S’=2πR=2.3.40 — ∆S’=240cm — como ela efetua 3 voltas — ∆S=3.240=720cm=7,2m — R- C
03- Para que a roda traseira efetue o maior número de voltas por cada pedalada, a diferença entre os diâmetros das coroas dianteira e traseira tem que ser o maior possível — R- A
04- Nos pontos de contato entre a prancha e os pontos da periferia de cada polia, a velocidade
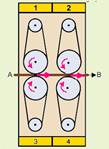
tangencial é a mesma tendo, em cada polia, o sentido em que a prancha está se movendo — R- C
05- Lembre-se que cos(0,06t) varia entre -1 e 1 — observe na expressão r(t)=5.865/[1 + 0,15.cos(0,06t)] que, terá valor máximo para um denominador menor e mínimo para um denominador maior — o valor máximo de r(t) ocorre quando cós(0,6t) for mínimo, ou seja, valer -1 — r(t)máximo=5.865/[1 + 0,15.cos(0,06t)]=5.865/[1 + 0,15.(-1)] — r(t)máximo=5.865/(1 – 0,15)=5.865/0,85 — r(t)máximo=6.900km (mais afastado da Terra) — o valor mínimo de r(t) ocorre
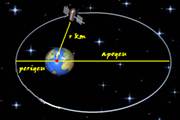
quando cos(0,6t) for máximo,ou seja, valer 1 — r(t)mínimo=5.865/[1 + 0,15.cos(0,06t)]=5.865/[1 + 0,15.(1)] — r(t)mínimo=5.865/(1 + 0,15)=5.865/1,15 — r(t)mínimo=5.100m (mais próximo da Terra) — o enunciado afirma que ele quer calcular a soma desses valores — S=rperigeu + rapogeu=5.100 + 6.900 — S=12.000km — R- B
06- O tempo em que a Lua demora para dar uma volta em torno da Terra (período de translação da Lua em torno da Terra), é o mesmo que ela demora para sofrer rotação em torno de si mesma (período de rotação da Lua) — R- C
07- Observe a figura abaixo:
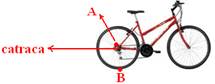
I- falsa — o ponto B está mais afastado do centro e VB > VA
II- correta — descrevem o mesmo ângulo no mesmo tempo
III- correta — demoram o mesmo tempo para efetuar uma volta completa
R-E
08- As velocidades escalares das periferias das rodas das bicicletas do pai e do filho são as mesmas — Vp=Vf — fpRp=ffRf — Rp=2Rf — fp.2Rf =ffRf — fp=ff/2 — R- A
09- Veja na expressão W=V/R, que W é constante (o eixo do carro gira com a mesma velocidade angular) e, assim, V é diretamente proporcional a R — como o diâmetro e consequentemente o raio teve um aumento de 10%, a velocidade também deverá ter o mesmo aumento, passando de 100km/h para 110km/h — R- C
10- Em um corpo em rotação todos os pontos apresentam mesmo período (T), frequência (f) e
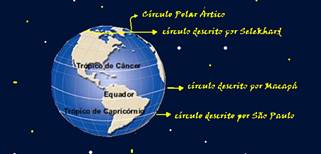
velocidade angular (ω), que são os mesmos que da Terra — TMacapá = TSão Paulo = T Selekhard — f Macapá = fSão Paulo = fSelekhard — W Macapá =WSão Paulo=W Selekhard — a velocidade escalar de um ponto é dado pela expressão v = W.r — como a velocidade angular é a mesma para todos os pontos, a velocidade escalar (intensidade da tangencial) será maior quanto maior for o raio (r) em relação ao eixo de rotação — VMacapá > VSão Paulo > VSelekhard — R- A
11- Observe que entre o primeiro e o segundo pentagrama a pá de cor diferente girou 3π/2 rad em t=1/24s — num período T ela gira 2π rad — regra de três — 3π/2 rad – t=1/24 s — 2π rad – T s — 3πT/2=2π/24 — T=4/72 — T=1/18s — f=1/T — f=18Hz — R- B
