Resolução Comentada – Hidrostática – Pressão Hidrostática

 Resolução Comentada

Hidrostática

Pressão Hidrostática

 

 

 01- A pressão no fundo do reservatório devida apenas à coluna líquida P_líquido=d_líquido.g.h é chamada depressão hidrostática e P=P_atm + d_líquido.g.h é chamada de pressão total, pressão absoluta ou simplesmente pressão  —  a pressão exercida por uma coluna líquida não depende das dimensões do recipiente que a contém, mas apenas da natureza do líquido, fornecida pela sua densidade (d), do local (g) e da altura da coluna (h)  —  o gráfico da pressão total P em função da altura “profundidade” h, (P=P_atm+ d.g.h, “ esta expressão é chamada de Teorema Fundamental da Hidrostática ou de Teorema de Stevin), que é uma função do primeiro  grau), é uma reta inclinada  —  portanto, a pressão

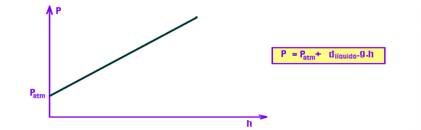
no fundo do recipiente varia linearmente com a altura e independe da área de seção reta de cada cilindro  —  R- A

02- Quando você abre a válvula, a água flui da caixa da esquerda para a da direita até que elas tenham a mesma altura  —  a altura da água na caixa da esquerda diminui e consequentemente a pressão na base da mesma também diminui  —  R- A

03- Teorema de Stevin  —  P= P_atm + dgh  —  4.10⁵ = 10⁵ + 10³.10.h  —  h=3.10⁵/10⁴  —  h=30m  —  para sofrer na subida vertical uma variação de pressão ΔP=10⁴N/m², em Δt=1s, ele deve se deslocar  —  ΔP=d.g.h  —  10⁴=10³.10.h  —  h=1m  —  V= ∆S/∆t  —  V=Δh/Δt  —  V=1/1  —  V=1m/s  —  R- D

04-  A  pressão do ar aprisionado no barco à profundidade h=(2,20 – 1,70)=0,5m é dada por P= P_atm + d.g.h  —  P – P_atm = d.g.h = 10³.10.0,5  —  P – P_atm=5,0.10³N/m²  —  R- A

05- A força  do jato de água da descarga faz com que a água da mesma flua rapidamente pelo sifão, levando os detritos embora  —  depois, a água volta a ficar na mesma altura no sifão e no vaso, pois os dois ficam sujeitos à mesma pressão (mesmo princípio dos vasos comunicantes), mantendo o nível da água constante e impedindo que o cheiro do esgoto invada o banheiro  —  

R- A

06- De acordo com Teorema de Stevin, pontos de mesmo líquido em repouso que estão na mesma horizontal estão sob mesma pressão — então, no ponto A da horizontal que passa pela interface entre a água e o líquido mais denso, a pressão deve ser a mesma que no ponto B

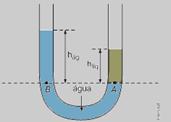
situado na água, na mesma horizontal  —  p_A = p_B  — d_água.g.h_água=d_líquido.g_..h_líquido  —  como d_líquido > d_água (dado do exercício)  —h_líquido < h_água  —  R- D

07-  Dados  —  d_água = 1 g/cm³ = 10³ kg/m³;  —  d_glic = 1,3 g/cm³ = 1,3.10³ kg/m³  —   h_água = 10 cm = 10^-1 m; h_glic = 1 m  —   g = 10 m/s²  —  p_atm = 1,01.10⁵ Pa  —  pressão da coluna de água  —  P_água=d_água.g.h_água=(10³).10.(10^-1)  —  P_água=1,0.10³Pa=0,01.10⁵Pa  —  pressão da coluna de glicerina  —  P_glic=d_glic.g.h_glic=(1,3.10³).(10).(1)  —  P_glic=1,3.10⁴Pa=0,13.10⁵Pa  —  na superfície que separa água-glicerina a pressão a pressão é P₁=P_atm+ P_água=1,01.10⁵ + 0,01.10⁵  —  P₁=1,02.10⁵Pa  —  no fundo do recipiente, a pressão é (p₂) e vale  —  P₂=P_atm + P_água + P_glic  —  P₂=1,01.10⁵ + 0,01.10⁵+ 0,13.10⁵   —  P₂=1,15.10⁵ Pa.  —  R- E

Obs: segundo o Sistema Internacional de Unidades o plural das unidades é feito apenas acrescentando a letra s no final, quando não terminada em s. Caso seja terminada em s, não sofre flexão, e quando grafadas por extenso, deve ser em letras minúsculas. Exemplos: pascal – pascals; decibel – decibels; newton – newtons.

08-  Dados: m = 900 kg; A₁ = 2.500 cm² = 25.10^-2 m² ; A₂= 25 cm² = 25.10^-4 m²; d_óleo = 900 kg/m³; h = 4m  —  de acordo com o teorema de Stevin, pontos de um mesmo líquido em repouso que estão na

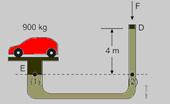
mesma horizontal suportam a mesma pressão  — a pressão no ponto (1) provocada pelo peso do carro é igual à pressão no ponto (2) provocada pela força  , somada à pressão da coluna líquida  —  P_r1=P_r2  —  P_esocarro/A₁=F/A₂ + d_´oleo.g.h  —  9000/25.10^-2=F/25.10^-4 + 900.10.4  —  36.000 – 36.000=F/25.10^-4  —  F=0  —  R- A

09- A diferença de pressão hidrostática (ΔP) entre dois pontos de desnível h, para um líquido de densidade d_líq, é dada pelo teorema de Stevin  —  ΔP = d_líq.g.h  —  assim,, essa diferença só depende da densidade do líquido, do desnível h e da gravidade local g  —   R- B

10- Dados  —  h = 2.000 m  —  g = 10 m/s²  —  ρ = 0,9 g/cm³ = 0,9.10³=9.10² kg/m³  —  teorema de Stevin  —  ∆P = ρ g h =9.10².10.2.10³  —  ∆P = 180.10⁵  —   ∆P = 1,8.10⁷ Pa  —  R- B

 Voltar para os exercícios