Experiência de Torricelli – Princípio de Pascal – Resolução
Resolução Comentada
Hidrostática
Experiência de Torricelli – Princípio de Pascal
01- Observe atentamente a figura que representa a experiência de Torricelli realizada ao nível do mar e leia com atenção o texto que a segue:
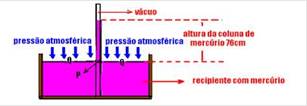
– Torricelli concluiu que a atmosfera exerce pressão sobre a superfície do mercúrio dentro do recipiente e como o mercúrio está em equilíbrio, a pressão no tubo ao nível P, (figura acima), é igual à pressão atmosférica no nível Q da superfície do líquido contido no recipiente.. Como na parte superior do tubo não há ar, a pressão no ponto P (pressão devida à coluna de mercúrio dentro do tubo) é igual à pressão no ponto Q (pressão atmosférica ao nível do mar). Portanto, a pressão atmosférica ao nível do ar corresponde à pressão que mantém uma coluna de mercúrio a uma altura de 76cm, ou 760mm ou ainda 0,76m. Lembrando que g=9,8m/s2 e que dmercúrio=13.600kg/m3, tem-se — PQ=PP — Patm=dmercúrio.g.h — Patm=13.600.9,8.0,76 — Patm=1,01N/m2 (Pa)
I. Falsa — como a pressão atmosférica é devido ao peso da coluna de ar, quanto maior a altitude
menor será esse peso e,consequentemente, menor será a altura da coluna que o equilibrará — a pressão atmosférica diminui com a altitude.
II. Correta — Se a experiência de Torricelli for realizada ao nível do mar, mas com água, cuja densidade é 13,6 vezes menor que a do mercúrio, a altura da coluna de água será aproximadamente igual a 10,3m, pois — Pmercúrio=dmercúrio.g.hmercúrio — Págua=dágua.g .hágua —
Pmercúrio= Págua — 13,6dágua.g.hmercúrio=dágua.g .hágua — 13,6.hmercúrio=hágua.
III. Correta — Torricelli fixou uma escala vertical graduada no tubo de mercúrio utilizado nesta experiência, obtendo desta forma o
aparelho de medição da pressão atmosférica, o barómetro de mercúrio — assim, barômetro é um
aparelho que mede pressão atmosférica,mas também serve para medir a altitude de um lugar, pois P=d.g.h é uma função também da altura h.
R- D
02- À medida que os sacos sobem sobe seu volume vai aumentando porque a diferença entre a pressão do ar dentro dos sacos e a pressão cada vez mais reduzida fora dela gera uma força resultante que empurra o plástico do saco de salgadinhos para fora —
R- B
03- Quanto maior a altitude, menor é a pressão e quanto menor a pressão menor é a temperatura de ebulição da água — R- A
Observação — a água, em pressões muito baixas, ferve à temperaturas bem inferiores à 100 °C — no princípio do funcionamento de uma panela de pressão, há o aumento da pressão atmosférica dentro da panela e isso faz com que o seu ponto de ebulição seja maior , podendo atingir temperaturas de até 120° da água e haja um cozimento mais rápido do alimento.
04- Qualquer que seja a natureza ou densidade do líquido, a superfície livre do mesmo fica a uma mesma altura h, nos dois compartimentos do bule (corpo principal e bico), em relação à linha de referência do sistema — isso ocorre porque a pressão exercida na superfície dos dois ramos do sistema de vasos comunicantes é a pressão atmosférica — R- C
05- Observe que os pontos M e N da figura abaixo estão numa mesma horizontal, suportando assim
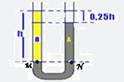
a mesma pressão — PM=PN — Patm +ρB.g.h = Patm + ρA.g.0,75h — ρB=0,75ρA — ρB/ρA=0,75 — R- A
06- Dados — h=10cm=0,1m — dA=5.103kg/m3 — dB=0,5.103kg/m3 — sendo a seção reta circular (S=1cm2=1,0.10-4m2) no diafragma a mesma nos dois lados, e como a densidade do líquido A é maior que a do líquido B, a intensidade da força resultante sobre o diafragma vale — FR=FA – FB — PA=FA/S — FA=PA.S — FB=PB.S — FR=PA.S – PB.S=S(PA – PB) — FR=S.(dA.g.h – dB.g.h) —
FR=1,0.10-4.(5.103.10.0,1 – 0,5.103.10.0,1) — FR=1.0.10-4.4,5.103 — FR=4,5.10-1N — FR=4.500.10-4N —R- D
07- Observe na figura abaixo que os pontos M e N na mesma horizontal suportam a mesma pressão –
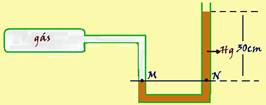
— PM=Pgás=PN — PN=Patm +d.g.h —Pgás=76cmHg + 30cmHg — Pgás=106cmHg — R- D
08- Princípio enunciado por Pascal, físico e matemático francês (1623 – 1663), conhecido como princípio de Pascal: “ O acréscimo de pressão exercido num ponto de um líquido ideal em equilíbrio é transmitida integralmente a todos os pontos desse líquido e também às paredes do recipiente onde está contido” — R- E
09- Princípio de Pascal: “ O acréscimo de pressão exercido num ponto de um líquido ideal em equilíbrio é transmitida integralmente a todos os pontos desse líquido e também às paredes do recipiente onde está contido” — então, a pressão em cada êmbolo a mesma — F1/A1=F2/A2 — F2/F1=A2/A1 — R- E
10- Princípio de Pascal — F2/A2=F1/A1 — F2/πR22=F1/πR12 — 2/π(5.10-3)2=F2/π(1.10-2)2 — F2=2.10-4/25.10-6 — F2=0,08.102 — F2=8N — essa força equilibra uma massa — p=Mg — 8=M.10 — M=0,8kg=800g — R- B
11- Pelo princípio de Pascal — PA=PB — FA/SA=FB/SB — FA/πD2=FB/π(4D)2 — FA/1=FB/16 — FA/FB=16 — R- A
12- Dados — F1 = 4.000 N — A1 = 10π cm2 — A2 = 0,05π cm2 — L = 1 m — m = 1 g = 10-3 kg —
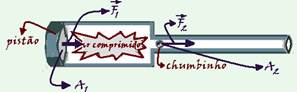
quando você aplica a força 
sobre o pistão de área A1, através do ar comprimido, transmite-se sobre o chumbinho de área A2, a força 
— a relação entre essas grandezas é dada pelo princípio de Pascal — F1/A1=F2/A2 — 4.000/10=F2/0,05 — F2=20N — essa força , também suposta constante, realiza trabalho sobre o chumbinho ao longo do cano da espingarda, aumentando sua velocidade a partir do repouso (vo = 0) — pelo teorema da energia cinética, considerando como a força resultante sobre o chumbinho — WF2=ΔEcinética — F2.d.cosα= Ecf – Eci — F2.L.1=mVf2/2 – 0 — 20.1=10-3.Vf2/2 — Vf=√(40 000) — Vf=200m/s — R- B
13- Dados: V = 1.200 L; h = 30 m; L = 200 m — seguindo as instruções do fabricante, entremos com os dados na tabela para obtermos o valor de H.
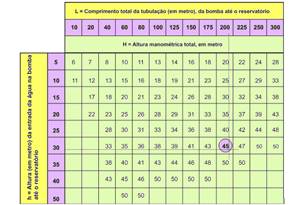
Como mostrado, obtemos H = 45 m — analisando o gráfico dado, temos os valores mostrados: H = 45 m — Q = 900 L/h.
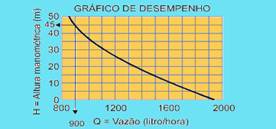
Calculando o tempo para encher o reservatório — Q=V/t — 900=1.200/t — t=1.200/900 — t=4/3h — t=80min — t=1h e 20min — R- E