Torricelli Experiment – Pascal’s Principle – Resolution – EN
Commented Resolution
Hydrostatics
Torricelli’s Experiment – Pascal’s Principle
01- Look carefully at the figure that represents Torricelli’s experiment carried out at sea level and read the text that follows it carefully:
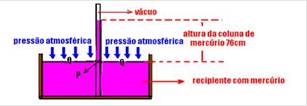
– Torricelli concluded that the atmosphere exerts pressure on the surface of the mercury inside the container and, as the mercury is in equilibrium, the pressure in the tube at level P (figure above) is equal to the atmospheric pressure at level Q of the surface of the liquid contained in the container. As there is no air in the upper part of the tube, the pressure at point P (pressure due to the column of mercury inside the tube) is equal to the pressure at point Q (atmospheric pressure at sea level). Therefore, the atmospheric pressure at air level corresponds to the pressure that maintains a column of mercury at a height of 76 cm, or 760 mm or 0.76 m. Remembering that g = 9.8 m/s 2 and that d mercury = 13,600 kg/m 3 , we have — P Q = P P — P atm = d mercury .gh — P atm = 13,600.9.8.0.76 — P atm = 1.01 N/m 2 (Pa)
I. False — since atmospheric pressure is due to the weight of the air column, the higher the altitude
the smaller this weight will be and, consequently, the smaller the height of the column that will balance it will be — atmospheric pressure decreases with altitude.
II. Correct — If Torricelli’s experiment is carried out at sea level, but with water, whose density is 13.6 times less than that of mercury, the height of the water column will be approximately equal to 10.3 m, since — P mercury = d mercury .gh mercury — P water = d water .g .h water —
P mercury = P water — 13.6d water .gh mercury =d water .g .h water — 13.6.h mercury =h water .
III. Correct — Torricelli fixed a graduated vertical scale to the mercury tube used in this experiment, thus obtaining the
atmospheric pressure measuring device, the mercury barometer — thus, a barometer is a
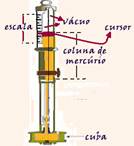
device that measures atmospheric pressure, but also serves to measure the altitude of a place, since P=dgh is also a function of the height h.
R-D
02- As the bags rise, their volume increases because the difference between the air pressure inside the bags and the increasingly reduced pressure outside generates a resulting force that pushes the plastic of the snack bag outwards —
R-B
03- The higher the altitude, the lower the pressure and the lower the pressure, the lower the boiling temperature of water — A- A
Note — water, at very low pressures, boils at temperatures well below 100 °C — when a pressure cooker starts to work, there is an increase in atmospheric pressure inside the pan and this causes its boiling point to be higher, reaching temperatures of up to 120 °C than water and cooking food more quickly.
04- Whatever the nature or density of the liquid, its free surface remains at the same height h, in both compartments of the teapot (main body and spout), in relation to the reference line of the system — this occurs because the pressure exerted on the surface of the two branches of the system of communicating vessels is atmospheric pressure — R- C
05- Note that points M and N in the figure below are on the same horizontal, thus supporting
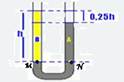
the same pressure — P M =P N — P atm +ρ B .gh = P atm + ρ A .g.0.75h — ρ B =0.75ρ A — ρ B /ρ A =0.75 — R- THE
06- Data — h=10cm=0.1m — d A =5.10 3 kg/m 3 — d B =0.5.10 3 kg/m 3 — the circular cross-section (S=1cm 2 =1.0.10 -4 m 2 ) in the diaphragm being the same on both sides, and since the density of liquid A is greater than that of liquid B, the intensity of the resulting force on the diaphragm is — F R =F A – F B — P A =F A /S — F A =P A .S — F B =P B .S — F R =P A .S – P B .S=S(P A – P B ) — F R =S.(d A .gh – d B .gh) —
F R =1,0.10 -4 .(5.10 3 .10.0,1 – 0.5.10 3 .10.0,1) — F R =1.0.10 -4 .4,5.10 3 — F R =4,5.10 -1 N — F R =4,500.10 -4 N — R- D
07- Observe in the figure below that points M and N on the same horizontal support the same pressure –
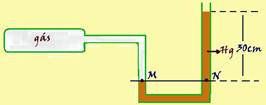
— P M =P gas =P N — P N =P atm +dgh —P gas =76cmHg + 30cmHg — P gas =106cmHg — R- D
08- Principle stated by Pascal, French physicist and mathematician (1623 – 1663), known as Pascal’s principle: “The increase in pressure exerted at one point of an ideal liquid in equilibrium is transmitted in full to all points of that liquid and also to the walls of the container where it is contained” — R- E
09- Pascal’s Principle: “The increase in pressure exerted at a point of an ideal liquid in equilibrium is transmitted in full to all points of that liquid and also to the walls of the container where it is contained” — therefore, the pressure on each piston is the same — F 1 / A 1 = F 2 / A 2 — F 2 / F 1 = A 2 / A 1 — R- E
10- Pascal’s Principle — F 2 /A 2 =F 1 /A 1 — F 2 /πR 2 2 =F 1 /πR 1 2 — 2/π(5.10 -3 ) 2 =F 2 /π(1.10 -2 ) 2 — F 2 =2.10 -4 /25.10 -6 — F 2 =0.08.10 2 — F 2 =8N — this force balances a mass — p=Mg — 8=M.10 — M=0.8kg=800g — R-B
11- By Pascal’s principle — P A =P B — F A /S A =F B /S B — F A /πD 2 =F B /π(4D) 2 — F A /1=F B /16 — F A /F B =16 — R- A
12- Data — F 1 = 4,000 N — A 1 = 10π cm 2 — A 2 = 0.05π cm 2 — L = 1 m — m = 1 g = 10 -3 kg —
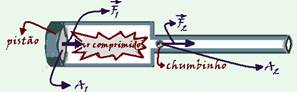
when you apply the force 
on the piston of area A 1 , through the compressed air, the force is transmitted to the pellet of area A 2 , the relationship between these quantities is given by Pascal’s principle — F 1 / A 1 = F 2 / A 2 — 4,000/10=F 2 /0.05 — F 2 = 20 N — this force , also assumed constant, does work on the pellet along the barrel of the shotgun, increasing its speed from rest (v o = 0) — by the kinetic energy theorem, considering the resulting force on the pellet — W F 2 =ΔE kinetic — F 2 .d.cosα= E cf – E ci — F 2 .L.1=mV f 2 /2 – 0 — 20.1=10 -3 .V f 2 /2 — V f =√(40,000) — V f =200m/s — R- B
13- Data: V = 1,200 L; h = 30 m; L = 200 m — following the manufacturer’s instructions, enter the data in the table to obtain the value of H.
As shown, we obtain H = 45 m — analyzing the given graph, we have the values shown: H = 45 m — Q = 900 L/h.
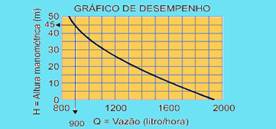
Calculating the time to fill the reservoir — Q=V/t — 900=1,200/t — t=1,200/900 — t=4/3h — t=80min — t=1h and 20min — R- E