Resolução Comentada – Gravitação Universal – Velocidade de escape e Aceleração da Gravidade

Resolução Comentada

Gravitação Universal

Velocidade de escape e Aceleração da Gravidade

 

 01- As leis de Kepler não justificam a afirmação do astronauta porque elas versam sobre forma da órbita, período da órbita e área varrida na órbita  —  a afirmação explica-se pelo Princípio Fundamental da Dinâmica, pois o que está em questão são a massa e o peso do telescópio  —  como o astronauta e o telescópio estão em órbita, estão sujeitos apenas à força peso, e, consequentemente, à mesma aceleração (centrípeta), que é a da gravidade local, tendo peso APARENTE nulo  —  F_R=P  —   m a = m g  —  a = g.

É pelo mesmo motivo que os objetos flutuam dentro de uma nave e diz-se nesse caso que os corpos estão em estado de  imponderabilidade (sensação de ausência de peso)  —  todavia, a sensação de “levitar” ocorre não por “ausência de peso, ou seja, falta de gravidade”, mas, sim, porque a nave e tudo o que se encontra no seu interior caem com a mesma velocidade vetorial e estão submetidos à mesma aceleração durante a queda    — isto significa que astronauta e nave ficam em repouso um em relação ao outro  —   R- D

Observação  —  considerando R = 6.400 km o raio da Terra, à altura h = 540 km, o raio da órbita do telescópio é r = R + h = 6.400 + 540 = 6.940 km  —  de acordo com a lei de Newton da gravitação, a intensidade do campo gravitacional num ponto da órbita é   —  g = g_o.(R/r)², sendo g_o= 10 m/s² (aceleração da gravidade na superfície da Terra)  —  g=10.(6.400/6.940)2² —  g=8,5m/s²  —  ou seja, o peso REAL do telescópio na órbita não é pequeno, é 85% do seu peso na superfície terrestre. 

02- A massa de qualquer corpo é a mesma na Terra, na Lua ou em qualquer outro planeta  —  peso do corpo na Lua  —  P_Lua=m_corpo.g_Lua  —  a intensidade da força de atração gravitacional, na superfície da Lua de raio R, entre esse corpo e a Lua é fornecida por F_G=G.M_Lua.m_corpo/R²  —  P=F_G  —  m_corpo.g_Lua = G.M_Lua.m_corpo/R²  —  g_Lua=G.M_Lua/R²=7.10^-11.7.10²²/(2.10⁶)²  —  g_Lua=1,2m/s²  — peso na Lua  —   P_Lua=m_corpo.g_Lua=80.1,2  —  P_{astronauta-Lua}= 96N  —  R- C

03- Na superfície da Terra  —  g_o=GM/R²  —  na altura h=2R + r=3R  —  g_h=GM/(3R)²  —  gh=GM/9R²  —  g_h=g_o/9 

R- E 

04- Velocidade de escape V_e  — velocidade mínima necessária para que um objeto, sem propulsão própria, saia da superfície da Terra ou de qualquer planeta, ou ainda, saia da altura R em relação ao centro da Terra ou do planeta  e chegue no infinito com velocidade zero  —  V_e=√(2GM/R)  —  M é a massa da Terra ou do planeta e R é a distância do centro da Terra ou do planeta até o ponto onde ele é lançado  —  substituindo os valores de G, M, e R (para a Terra) que conhecemos, obtemos:V_e≈11,3km/s que é a velocidade com que um corpo, sem propulsão própria deve sair da superfície da Terra para “libertar-se” de seu campo gravitacional  —  o valor da velocidade de escape não depende da massa do corpo que está sendo lançado mas apenas da massa do corpo central, no caso, a Terra e também não depende do ângulo de lançamento  —   em função da aceleração da gravidade g, a velocidade de escape será dada por:

g=GM/R²   e  V_e=√(2GM/R)  —   V_e=√(2gR²/R)  —  V_e=√(2gR)  —  V_e=√(2.3.500.10³)=√(30.10⁵)  —  V_e=√(3.10⁶)=√(3).10³m/s  –V_e=√3 km/h  —  R- 5

05- Devido ao movimento de rotação da Terra e ao fato da Terra ser achatada nos pólos e dilatada no equador, o valor de g e, consequentemente do peso de um corpo, é máximo nos  pólos (9,823m/s²) onde não há influência da rotação da Terra e mínimo no equador (g=9,789m/s²) onde essa influência é máxima  —   como a massa de um corpo é invariável, o mesmo ocorre com o peso. Anote que o peso é o mesmo no Polo Norte e no Polo Sul  —  latitude é definida como sendo a medida angular ao longo de um

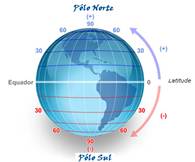
meridiano, do equador até os polos da Terra, na direção norte ou sul, variando de latitude zero (no equador) a latitude 90^o (nos polos)  —  R- C

06- Leia atentamente as informações abaixo  —   imponderabilidade é a sensação de ausência de peso  —  um astronauta dentro da nave espacial e a própria nave tem a mesma velocidade orbital  V  e a mesma aceleração de queda g (queda livre), pois as órbitas são de mesmo raio  —  assim, astronauta, nave, e tudo mais no veículo ficam em repouso uns em relação aos outros e o

é apenas sensação, pois ali existem  e , caso contrário eles não estariam em órbita circular, mas sim em MRU, fora do campo gravitacional terrestre  —  observe pela figura abaixo que eles

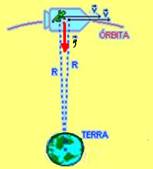
(astronauta e nave) estão sempre caindo sobre a Terra  mas não a atingem por causa da velocidade tangencial .

R- C

07- Do enunciado  —  M_G=3M_T  —  r_G=0,2r_T  —  T=37 dias  —  V_G=0,5V_T  —  r (raio da órbita)  —  R (raio do planeta)

I. Falsa  —  você deve calcular a aceleração da gravidade de cada planeta e depois iguala-las  —  g_G=GM_G/R²_G=G3M_T/R²_G  —  g_T=GM_T/R²_T  —  g_G=g­_T  —  3GM_T/R²_G=GM_T/R²_T  —  3/R²_G=1/R²_T  —  R_G=√(3.R_T)  — R_G=1,73R_T (deve ser 1,73 vezes maior).

II. Verdadeira  —  velocidade orbital  —  V=√(GM/r)  —  V²=GM/r  —  r_G – distância de Gleese 581g à estrela  —  r_T  —  distância da Terra ao Sol  —  velocidade orbital de Gleese 581g  —  V²_G=GM_estrela/r_G  —  (0,5V_T)2=GM_estrela/0,2r_T  —  0,25VT2=GM_estrela/0,2r_T  —  V²_T=GM_estrela/0,05r_T (I)  — velocidade orbital da Terra  —  V²_T=GM_Sol/r_T (II)  —  igualando (I) com (II)  —  GM_estrela/0,05r_T=GM_Sol/r_T  —  M_estrela=0,05M_Sol=5%M_Sol (menos que a metade).

(III) Correta  —  uma face é sempre clara e a outra sempre escura  —  o tempo que Gleese demora para efetuar uma volta completa em torno de si mesma (mesmo período, mesma velocidade angular) é o mesmo que Gleese demora para efetuar uma volta completa ao redor de sua estrela.

(IV) Falsa  —  W=V/r  —  W_G=V_G/r_G=0,5V_T/0,2r_T  —  W_G=2,5V_T/r_T  —  W_G=2,5W_T (é maior)

 R- C

08- Relação entre as alturas  —  sendo g_L a aceleração da gravidade na Lua e g_T a aceleração da gravidade na Terra  —  aplicando a equação de Torricelli  —  V²=V_o² + 2gh  —  V_o=0 (partem do repouso)  —  V²=2gh  —  na Lua  —  V_L²=2g_Lh  —  na Terra  — 

V_T²=2g_Th  —  observe nessas duas expressões que, como a altura h é a mesma, as velocidades na Lua e na Terra são diferentes e, consequentemente as energias cinéticas também  —  sendo g_L<g_T, isso implica em que V_L<V_T  —  assim, ele chegará com energia cinética menor na Lua   —  relação entre os tempos de queda  —  na queda livre  — h =gt²/2  —  t=√(2h/g)  —  observe que o tempo de queda é inversamente proporcional a √g  —  como g_L < g_T, o tempo de queda na Lua é menor do que na Terra  —  R- A

09- I) Falsa – a força que age sobre ele é a força resultante centrípeta que é igual à força gravitacional  —    II) Correta – vide I  — III) Falsa – exerce sim, pelo princípio da ação e reação  —   IV) Verdadeira  —  V=√(GM/R) – V e R são inversamente proporcionais, ou seja, à medida que a velocidade V vai diminuindo, a altura R também vai diminuindo e ele irá caindo.

R- D

10- Enunciado da lei da gravitação universal de Newton  —  “matéria atrai matéria com forças cujas intensidades são diretamente proporcionais ao produto de suas massas e inversamente proporcionais ao quadrado da distância que os separa”

a) Falsa  —  essa constante, representada por G, pode ser chamada de constante de gravitação universal ou de constante de Gauss  —  G é não é dependente dos corpos que se atraem, nem da distância ou até mesmo do meio interposto entre os dois corpos, sendo assim uma constante universal.
b) Falsa  —  ambos se atraem,  mas a intensidade dessa força consegue atrair apenas o objeto e não a Terra por causa da

diferença de massa entre eles.

c) Falsa  —  o satélite só fica em órbita se estiver dentro da campo gravitacional terrestre e, nesse caso, a força gravitacional é a própria força resultante centrípeta.

d) Falsa  —  diminui sim, mas não linearmente,pois, é inversamente proporcional ao quadrado da distância (função do segundo grau)

e) Correta  — o peso de um corpo é resultado da força de atração entre ele e o centro da Terra e P=m.g

R- E

 

Voltar para os exercícios