Resolução Comentada – Leis de Kepler
Resolução Comentada
Leis de Kepler
01-

Observe na expressão acima que as áreas “varridas” são diretamente proporcionais aos intervalos de tempo gastos para “varre-las” — o tempo gasto pela Terra para “varrer” a área inteira (S) da elipse, ou seja, para efetuar uma volta completa é de 1 ano terrestre (12 meses) — o tempo gasto para “varrer” um quarto dessa área (S/4) será 12/4=3 meses — R- D
02- Pela representação fornecida você não consegue se basear no tamanho (diâmetro) dos satélites, pois são todos do mesmo tamanho — então você deve se basear na distância entre Júpiter e esses satélites — de acordo com a terceira lei de Kepler (lei dos períodos): “ Os quadrados dos períodos T de revolução dos planetas (tempo que demora para efetuar uma volta completa em torno do Sol) são proporcionais aos cubos das suas distâncias médias R ao Sol” — T2/R3=constante=K’ — observe que a medida que R aumenta, T também aumenta, o que significa que quanto mais afastado o planeta estiver do Sol maior será seu ano (tempo que demora para dar um volta completa ao redor do Sol), o que é fornecido pela tabela — observe também pela tabela que a reta que corresponde as medidas das distâncias dos satélites ao centro do planeta Júpite indicam que as distâncias da menor para a maior são, respectivamente — 2 corresponde a Io; 3 corresponde a Europa; 1 corresponde a Ganimedes; 4 corresponde a Calisto — 2,3,1,4 — como a sequência pedida no exercício é 1, 2, 3 e 4, a resposta correta é dada por — 1 = Ganimedes; 2 = Io; 3= Europa e 4 = Calisto — as possibilidades fornecidas indicam que a resposta correta corresponde a alternativa b — R- B
03-

Observe na expressão acima que as áreas “varridas” são diretamente proporcionais aos intervalos de tempo gastos para “varre-las” — De 1o de Abril a 30 de Maio = 60dias — regra de três — 365 dias – 6,98.1022 m2 — 60 dias – A — A=60 x 6,98.1022/365 — A≈1,14.1022m2 — R- A
04- Pela segunda lei de Kepler: “ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas proporcionais aos tempos gastos para percorrê-las” você conclui que tOP = tMN — observe que, como A1=A2, ∆tOP= ∆tMN, ou seja, para o arco maior OP, ser percorrido no mesmo intervalo de tempo que o arco menor MN, a velocidade em OP (mais perto do Sol – periélio) deve ser maior que a velocidade em MN (mais afastado do Sol – afélio) — VOP > VMN — R- B
05- a) Falsa — a expressão T2/R3=K, observamos que a medida que a distância R do planeta ao Sol aumenta, seu período T (tempo que demora para efetuar uma volta completa ao redor do Sol) também aumenta, o que significa que quanto mais afastado o planeta estiver do Sol maior será seu ano (tempo que demora para dar um volta completa ao redor do Sol — observe também que, nessa expressão o período independe da massa do Sol ou do planeta.
b) Falsa — o correto é — a razão entre o quadrado do seu período e o cubo do raio médio da órbita é uma constante de movimento.
c) Falsa — no Afélio, onde está mais afastado do Sol sua velocidade é menor que no Periélio onde está mais próximo do Sol.
d) Falsa — no Afélio, o planeta está mais afastado do Sol e, portanto tem menor velocidade e consequentemente menor energia cinética.
e) Correta — no Afélio, onde está mais afastado do Sol sua velocidade é menor que no Periélio onde está mais próximo do Sol.
d) Falsa — no Periélio ou Perigeu, o planeta está mais próximo do Sol e, portanto tem maior velocidade e consequentemente maior energia cinética.
R- E
06- I. Falsa — o verão não ocorre quando a Terra está no periélio (mais próxima do Sol) e nem o inverno quando ela está no afélio (mais afastada do Sol). As estações ocorrem devido ao fato de áreas da Terra, devido à inclinação da mesma, receberem mais ou menos luz do Sol durante seu movimento de translação.
II. Correta — ao efetuar um volta completa ao redor do Sol num período (ano) T um planeta percorre a distância ∆S=2πR e o seu perído (tempo que demora para efetuar uma volta completa é T — sua velocidade orbital vale V=∆S/T — T=2πR/V, que substituída em T2/R3=K nos fornece 4π2R2/V2R3=K — V2=4π2/KR — V=constante/R –observe nessa expressão que a velocidade V é inversamente proporcional à distância R ou seja, quanto mais afastado o satélite ou planeta estiver, menor será sua velocidade orbital.
III- Falsa — a terceira lei de Kepler (lei dos períodos) afirma: “ Os quadrados dos períodos T de revolução dos planetas (tempo que demora para efetuar uma volta completa em torno do Sol) são proporcionais aos cubos das suas distâncias médias R ao Sol” — este enunciado não se refere ao período de rotação (em torno de si mesmo, dia do planeta) — atualmente comprova-se que cada planeta tem um dia de duração própria, que dependerá de sua velocidade de rotação e de seu diâmetro.
R- C
07- Da 3ª lei de Kepler: o quadrado do período de translação (ano do planeta) é diretamente proporcional ao cubo do raio médio da órbita — T2 = k r3, podemos concluir que quanto mais distante do Sol orbitar o planeta, mais longo é seu ano — portanto, os chamados planetas internos, Mercúrio e Vênus, têm anos mais curtos do que o ano terrestre — R- D
08- Observe pela figura abaixo que, se o efeito da gravitação deixasse de existir, o planeta sairia
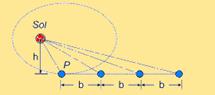
pela tangente entrando em movimento retilíneo uniforme, percorrendo sempre a mesma distância b em temos iguais, portanto varrendo a mesma área A, tal que — A = b.h/2 (I) — como o movimento é uniforme (ele se move por inércia, com velocidade constante V) — b=V.∆t (II)
— substituindo (II) em (I) — A=V.∆t.h/2 — A/∆t=V.h/2 — como V e h são constantes — A/∆t=constante, ou seja, ele continua varrendo áreas iguais em tempos iguais — R- A
09- O ano terrestre é o período de translação da Terra em torno do Sol (tempo que a Terra demora para efetuar uma volta completa ao redor do Sol) — se a nova órbita fica mais perto do Sol — r’ < r — usando a 3ª lei de Kepler — (T’/T)2=(r’/r)2 — observe nessa expressão que se r’< r — T’< T — o que torna o ano terrestre mais curto — o período aproximado do ciclo lunar é T = 27 dias — o novo período é T’ = 80 dias — usando novamente a 3ª lei de Kepler — (r’/r)3=(80/27)2 — r’≈![]() — r’≈2r — R- B
— r’≈2r — R- B
