FORÇAS NO MOVIMENTO CIRCULAR – Resolução

Resolução Comentada

FORÇAS NO MOVIMENTO CIRCULAR

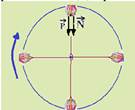
01- Observe na figura da direita que o pequeno bloco preso à extremidade do fio, chamado de “peso” descreve uma circunferência em um plano horizontal  —  nesse caso, surge sobre ele uma força resultante centrípeta  —  a força que faz a garrafa subir é a tração que age sobre a garrafa produzindo seu deslocamento vertical para cima e, ela pode ser considerada como uma parcela da força resultante centrípeta  —  R- D

02-  Tanto no ponto mais alto (A) como no ponto mais baixo (B) as forças que agem sobre o carvão  são, seu peso  constante, vertical e para baixo e a força de compressão  que o carvão troca com a superfície interna da lata para baixo em (A) e para cima em (B).

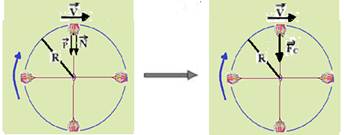
Em (A), ponto mais alto, a força resultante centrípeta  , que é dirigida sempre para o centro da circunferência, no caso, para baixo, é a soma vetorial de  com , de intensidade  —  F_c=P + N  —  m.V²/R=m.g + N  —  N=m(g + V²/R). É o mesmo resultado obtido quando um veículo passa por uma lombada ou quando um piloto de avião se encontra na parte mais alta de um looping vertical.

Substituindo os dados do exercício na expressão V=√(Rg)=√(0,8.10)  —  V=√8  —  V=2√2m/s  —  R- C

03- Na parte mais baixa da trajetória as forças que agem sobre a lata são seu peso  (vertical e para baixo) e a força de tração na

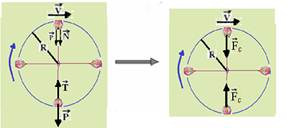
corda  (vertical e para cima)  — a intensidade de  deve ser maior que a intensidade de , pois a força resultante centrípeta  deve ser vertical e para cima, ou seja, dirigida para o centro da circunferência  —  R- A

04- Dados  —  n=4 rotações  —  ∆t=1s  —  W=n.360/∆t  —  W=4.360/2  —  W=720 ^o/s  —  R- B

05-  Dados  —  v_o = 0  —   m = 1.000 kg  —   H = 30 m  —   d = 20 m  —  r = 10 m  —  observe a figura

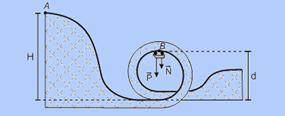
abaixo  —  cálculo da velocidade no ponto B pela conservação de energia mecânica  —  E_MA=E_MB  —mgH=mgd + mV²/2  —  V²=2h(H – d)  —  V²=20.(30 – 20)  —  V²=200  —  no ponto B, a resultante das forças que agem sobre o carro são radiais, portanto a aceleração é centrípeta  —  a=ac=V²/R=200/10  — a=20m/s².

No ponto B, a resultante é centrípeta e a força vertical que o trilho exerce no carro é a normal   —  no ponto B a força resultante centrípeta tem direção vertical e sentido para baixo (centro da circunferência)  —  F_c=N + P=ma  —  N + P=ma  —  N=ma – mg  —  N=1.000(20 – 10)  —  N=10.000N  — R- C

06- Conforme o diagrama anexo, as forças que agem no carro são o peso  e a normal . Como o movimento é circular e uniforme, a resultante dessas forças é centrípeta (radial), .

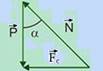
tgα = F_c/P=m.a_c/mg  —  a_c=g.tgα  —  como a e g são constantes, a aceleração centrípeta (radial, dirigida para o centro) tem módulo constante  —  R- D

07- O objeto solto bem como o próprio satélite está sujeito à força gravitacional terrestre e logo ambos têm peso  —  admitindo que o movimento do satélite e do corpo são circulares e uniformes, a aceleração centrípeta será a aceleração gravitacional  —  a alternativa c é falsa, pois se uma pessoa estiver solta dentro da nave ela não experimenta sensação de peso, mas está sujeito à aceleração gravitacional  —  R- B

08- O dinamômetro indica a intensidade da força de tração  no fio em cada caso  —  na figura (I),

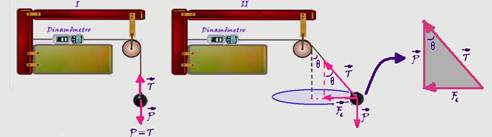
supondo o corpo em equilíbrio, a intensidade da força de tração  será a mesma que a do peso   — na figura (II), pêndulo cônico com o corpo girando com velocidade angular constante  —  colocando as forças do lado direito, a soma vetorial de  com  fornecerá a força resultante centrípeta   —   =  +   —  observe na figura (II) no triângulo hachurado da direita que T=P/cosθ —  como cosθ<1  —  T>P  —  a intensidade de , que representa a indicação do dinamômetro é maior que o peso do corpo  —  R- C

09- Para que o astronauta permaneça na mesma posição “colado” à nave, ele deve ter a mesma velocidade angular W que ela e também o mesmo período T (tempo que ela demora para efetuar uma volta completa), que é de 20s.

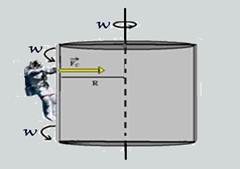
T=20s  —  W=2π /T  —  W=2π /20= π /10  —  W= π /10rad/s  —  F_c=m.W².R  —  F_c=70.( π /10)².10  —  F_c=7π² N  —  R- E

10- A força resultante centrípeta  , que é dirigida sempre para o centro da circunferência, no caso,

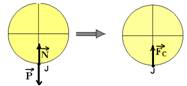
para cima, é a diferença vetorial entre  e  , de intensidade  —  F_c=N – P  —   m.V²/R= N – m.g  —  N=m.g + mV²/R  —  N=50.10 + 50.100/2  —N=3.000N  —  N= 3,0.10³ N  —  R- A

11-  Sendo o movimento circular a força resultante sobre a mosca é a centrípeta de direção radial, sentido para o centro da circunferência e intensidade F_c=m.V²/R  —  como m e V são constantes, F_c e R são inversamente proporcionais, ou seja, quanto menor é o raio R, maior será a intensidade da força resultante centrípeta   —   R- D 

Voltar para os exercícios