Resolução Comentada
Estático de um corpo extenso
01- Observe na figura abaixo que a força peso
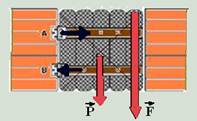
vertical e para baixo) tendem a fazer o portão girar no sentido horário, fazendo-o puxar a dobradiça em A (tentando arrancá-la) e comprimi-la em B — R- A
02- bandeja – b mb=0,4kg — prato -A – – mA=0,5kg — copo – B – mB=0,1kg — garrafa – C – mC=1,0kg — cálculo da abscissa do centro de massa — XCG=(mb.Xb + mA.XAA + mBXB + mCXC)/(mb + mA + mB + mC)= (0,4..0 + 0,5.(-2). + 0,1.(-10) + 1.(+4+)/(0,4 + 0,5 + 0,1 + 1,0)=2/2 — XCG=1cm — cálculo do centro de massa da ordenada — YCG=(mb.Yb + mA.YA +
mBYB + mcYc)/(mb + mA + mB + mC)=(0,4.0 + 0,5.(-5) + 0,1.5 + 1.4)/2 — YCM=2/2 — YCM=1cm — CG (1,1) — R- E
03- A figura mostra as abscissas x1; x2; x3 e x4 e as ordenadas y1; y2; y3 e y4 dos quatro corpos; a abscissa X e a ordenada Y do centro de massa:
R – C
04- Sem as moedas o centro de gravidade do sapinho está em seu próprio corpo — quando você
coloca as moedas em suas patas dianteiras e o apoia no lápis, essas duas moedas deslocam seu centro de gravidade para baixo de seu corpo e ele fica em equilíbrio estável — R- D
Observação: No boneco “João Bobo”, existe uma grande massa (contrapeso, normalmente chumbo), na parte inferior do brinquedo, fazendo com que seu centro de gravidade esteja bem
embaixo e ele fique em equilíbrio estável — quando você o retira da posição de equilíbrio estável, a tendência do contrapeso é retornar novamente ao equilíbrio, oscilando até que o contrapeso fique novamente em sua parte inferior.
05- Como o centro de gravidade CG está sempre no ponto médio e à medida que o cigarro vai queimando ele se desloca para a esquerda, quando o cigarro estiver na iminência de cair, você terá a situação da figura abaixo, onde você deve
observar que o cigarro queimou d=80 – 50=30mm com velocidade de 5mm/min — V=d/t — 5=30/t — t=6 min
R- C
06- Trata-se de corpos apoiados — situação I — como os três ângulos são de 120o o centro de gravidade CG está na junção – indiferente — situação II — o centro de gravidade CG está acima da
junção – instável — situação III — o CG centro de gravidade está abaixo da junção – estável —
R- E
07- A porta gira no sentido daquele que aplicar o maior momento na mesma — momento da força aplicada pelo homem — Mh=+Fh.d =80.10 — Mh=800N.cm — momento da força aplicada pelo menino — Mm=-Fm.d= -5.200 — Mm= – 1.000N.cm — ganha o menino — R- B
08- O jovem consegue soltar o parafuso, fazendo a chave girar quando o momento da força por ele
aplicada (Fj=75.10=750N)valer — MFj=F.d=750.20 — MFj=15.000N.cm — momento da força (F=51.10=510N) aplicada pela namorada — MFn=F.d=510.30 — MFn=15.300N — observe que o momento (torque) da força aplicada pela namorada é maior que o momento da força aplicada pelo jovem — sim, ela consegue soltar o parafuso.
09- Observe a figura abaixo — equilíbrio de translação do andaime (corpo extenso) — a resultante
das forças na vertical deve ser nula,e, para que isso ocorra — TE + TD=P — equilíbrio de rotação ( o andaime não deve girar) — a soma dos momentos de cada força deve ser nula — pólo em P — +TE.(x) – TD.(y)=0 — TE.(x)=TD.(y) — observe que, como x>y, TE deve ser menor que TD — TE<TD — R- C
10- Como é uma situação de equilíbrio de um corpo extenso, temos que considerar equilíbrio de translação (a resultante das forças deve ser nula) e equilíbrio de rotação (o momento resultante deve ser nulo). Analisando cada uma das opções:
a) Falsa — a resultante das forças na direção horizontal é não nula, não havendo, portanto, equilíbrio.
b) Falsa — a resultante das forças na direção vertical é não nula.
c) Correta — a força resultante pode ser nula bem como o momento resultante — trata-se de uma situação de possível equilíbrio
d) Falsa — o momento resultante é não nulo, provocando rotação no sentido horário.
R- C
11- Colocando as forças que agem sobre a trave — equilíbrio de rotação — a somatória dos
momentos de todas as forças deve ser nula — pólo em C — – F1.d1 + F.d – F2.d2 + F3.d3 = 0 — – 400.(0,2 + 0,1 + 0,3) + F.(0,1 + 0,3) – 400.(0,3) + 400.(0,3) = 0 —- 400.0,6 + F.0,4 – 400.0,3 + 400.0,3 = 0 — F=240/0,4 — F= 600N — R- E
12- Para que a escada não escorregue e caia, no apoio inferior tem que ter atrito, o que não precisa ocorrer no apoio superior — como a parede é lisa, ou seja, no ponto M não existe atrito — a figura abaixo mostra as três forças que agem sobre a escada que
está em equilíbrio —
13- Observe a figura abaixo — colocando o polo em N2 — a soma dos momentos em relação ao
polo deve ser nula — MN2=— MP=+P.4 — MN1=-N1.6 — MN1=-6.105N.m — +4P – 6.105=0 — P=6.104/4 — P=1,5.105N — a resultante das forças verticais deve ser nula — N1 + N2=1,5.105 — 1,0.105 + N2=1,5.105 — N2=0,5.105 — N2=5,0.104N — R- A
14- Observe o comprimento das hastes em relação ao ponto de apoio e verifique que o lado de comprimento 5cm deve equilibrar o dobro da massa que o lado de comprimento 10cm (figura abaixo)
R- C
15- Colocando o polo em N e calculando, calculando o momento de cada força, somando-os e
igualando-os a zero — -200.2 + F.0,5 + 350.1=0 — -400 + 0,5F + 350=0 — F=100N — R- D
16- Observe a relação F2/F1=d1/d2 — se d1 > d2 — F2 > F1 — R- C