Estática de um Ponto Material – Resolução

Resolução Comentada

Estática de um Ponto Material

01- Observe nas figuras abaixo  —  (1)  —  2T₁=P  —  T₁=P/2  —  (2) 2T₂sen60^o=P  —  T₂=P/2sen60^o  — 

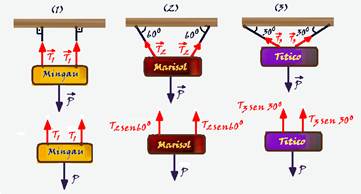
—  T₂=0,58P  —  (3) 2T₃sen30^o=P  —  T₃=P/2sen30^o  —  T₃=2P/2=P  —  R- B

Observação: Note que quanto menor for o ângulo com o teto, maior será a força de tração no fio.

02- Colocando as forças em cada fio e decompondo-as  —  equilíbrio na horizontal  — 

     

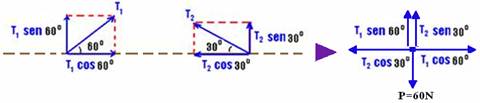
T₁cos60^o=T₂cos30^o  —  T₁.1/2=T₂.√3/2  — T₁=√3.T₂  —  equilíbrio na vertical  —  T₁sen60^o + T₂sen30^o=P  —  T₁.√3/2 + T₂.1/2=6.10  —  (√3.T₂.√3)/2 + T₂/2=60  —  3T₂ + T₂=120  —  T₂=30N  —  T₁=√3.T₂  —  T₁=√3.30  — T₁=30√3N

R- B

03- Observe a figura abaixo  —  P=mg=60.10  —  P=600N  —  como ele está em equilíbrio a intensidade da força resultante deve

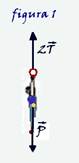
ser nula  —  F_R=0  —  2T₁=P  —  2T₁=600  —  T₁=300N.

Observe a figura abaixo onde as duas cordas foram prolongadas até se encontrarem:

R- E

04- Para que as placas fiquem em equilíbrio estático, resultante das forças que agem sobre elas devem ter componentes na horizontal e na vertical para que possam se anular  —  observe que a única alternativa que não tem componentes que possam se anular na horizontal é a V  —  R- E

05- Considere: sen 45º = 0,7; cos 45º = 0,7; sen 37º = 0,6 e  cos 37º = 0,8

Observe a figura abaixo onde foram decompostas as força T₁ e T₂  —  Equilíbrio na horizontal

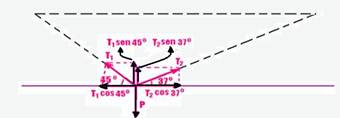
 T₁cos45^o=T2cos37^o  — T₁.0,7=T₂.0,8  —  T₁=8T₂/7  —  equilíbrio na vertical  —  T₁sen45^o + T₂sen37^o =P  —  T₁.0,7 + T₂.0,6=280  —  (8T₂/7).0,7 + 0,6T₂=280  —  0,8T₂ + 0,6T₂=280  —  T₂=280/1,4  —  T₂=200N  —  R- C

06- Observe a figura abaixo onde as forças de tração foram decomposta na vertical  — no equilíbrio a força resultante é nula  —  F_R=0

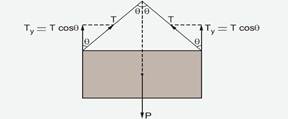
P=2Tcosθ  —  T=P/2cosθ  —  observe nessa expressão que a tração T é inversamente proporcional a cosθ, ou seja, quanto menor cosθ, maior será T e isso acontece quanto maior for o ângulo α  —  R- A

Observação  —  volte ao exercício 1 e veja que são situações diferentes.

07- Observe o diagrama abaixo que mostra as forças atuantes no terceiro elo  —  Dados  —   m = 200 g = 0,2 kg  —   g = 10 m/s² 

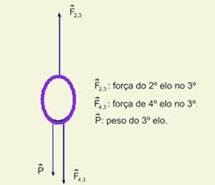
— P = m g = 0,2(10)  —  P = 2 N  (peso de cada elo) — F₄₃ = 2 P = 4 N  —  F₂₃ = 3 P = 6 N  —  R- B

08-  Observe nas figuras abaixo onde cada força de tração é decomposta na vertical (T_v=Tsen60^o) e na horizontal (T_h=Tcos60^o). 

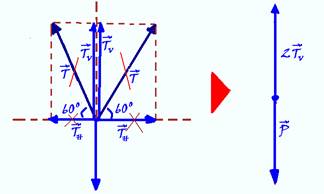
Como o sistema está em equilíbrio, as componentes horizontais se anulam e na vertical você terá  —  2T­_v=P  —  2Tsen60^o=P  —  2T.√3/2=50  —  T=50/√3N  —  R- C

 

Voltar para os exercícios