Resolução Comentada
Eletrostática
Campo Elétrico – Potencial Elétrico
01-(ENEM-MEC)
A despolarização ocorre na fase em que o potencial atinge o limiar (linha tracejada) e sobe, que é a fase 0 — repolarização ocorre quando o potencial está voltando ao potencial de repouso, o que ocorre na fase 3.
R- B
02- (ENEM-MEC)
Poder das pontas – se o campo elétrico que está próximo das pontas de certo condutor estiver muito intenso com uma quantidade maior de cargas elétricas, ele pode ionizar os átomos dos
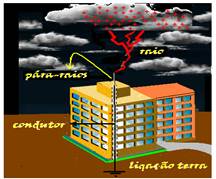
elementos que formam o ar, que passa a não ser mais um isolante, tornando-se assim um condutor elétrico, e o condutor se descarrega através das pontas. Esse fenômeno é chamado poder das pontas e é baseado nele o funcionamento dos pára-raios — portanto, nas pontas de um condutor eletrizado, encontramos uma quantidade maior de cargas por unidade de área — R- A.
03-(ENEM-MEC)
Blindagem eletrostática – Se, no interior de um condutor oco em equilíbrio eletrostático o campo elétrico
Foi adaptada para proteger instrumentos e aparelhos de grande sensibilidade colocados em seu interior. Observe na figura abaixo que a esfera do pêndulo eletrostático quando está no interior da gaiola, não sofre influências elétricas da esfera externa eletrizada.
A blindagem eletrostática (gaiola de Faraday) também é utilizada nos carros e aviões, oferecendo
proteção contra descargas elétricas. Construções também são feitas utilizando blindagem eletrostática, a fim de proteger seus equipamentos elétricos e eletrônicos
R- B
04-(UERJ-RJ)
A intensidade da força f entre duas cargas elétricas iguais q separadas por uma distância r é fornecida por f=k.q.q/r2 — entre as cargas 2q e 3q separadas pela mesma distância r será — f’=k.2q.3q/r2=6k.q.q/r2=6f — f’=6f — R- E.
05-(FGV-SP)
Força elétrica — Fe=KQq/d2 — força gravitacional — FG=GMm/d2 — igualando-as — KQq/d2 = GMm/d2 — KQ2/d2 = GM2/d2 — M2Q2=KG — MQ=√(KG) — R- C
06- (UFPE-PE)
Quando r=3m — F=2,5.10-4N — F=KQq/r2 — 2,5.10-4=9.109.Q.Q/32 — Q2=2,5.10-13=25.10-14 — Q=5.10-7C — R- E
07-(UFG-GO)
Observe as figuras abaixo:
R- D
08-(FGV-SP)
Em cada uma das extremidades das quatro diagonais que passam pelo centro do cubo há duas
cargas de mesmo módulo e de mesmo sinal. Elas exercem na carga central (também de mesmo sinal e mesmo módulo que as dos vértices) forças de mesma intensidade e de sentidos opostos. Portanto, essas forças se equilibram, sendo então nula a resultante dessas forças.
R- A
09-(FUVEST-SP)
I. Certo — só surge força sobre a carga se existir campo elétrico que origina essa força.
II. Certo — se não tiver carga, pode existir o campo elétrico sem existir força elétrica.
III. Errado — não surgirá força sobre a carga se não houver campo elétrico
R- D
10-(UCSal-BA)
O ponto P onde o campo elétrico resultante deve se anular deve estar à direita de Q (observe
figura) — a carga – 4Q cria campo de aproximação e a carga + Q, de afastamento — E1=K4Q/d2 — E2=KQ/(d – 3)2 — E1=E2 — 4KQ/d2=KQ/(d – 3)2 — (d – 3)2/d2=1/4 — (d – 3)/d=1/2 — d=6 unidades — é nulo no ponto 10.
R- A
11-(FUVEST-SP)
A única alternativa em que o objeto com carga positiva não é desviado (força resultante nula) durante a queda é a E (veja figura abaixo):
E (veja figura acima).
R- E
12-(FUVEST-SP)
Os nêutrons não sofrem desvio e o campo elétrico desvia os prótons para baixo (são repelidos pela placa positiva) R- E
13-(UFMS-MS)
R- C — os dipolos estão flutuando — as forças peso e elétrica se anulam — observe que os dipolos ficarão alinhados predominantemente na direção vertical com as cargas negativas voltadas para baixo (repulsão) e as positivas para cima (atração)
14-(FATEC-SP)
Comentário: materiais metálicos apresentam maior condutividade elétrica, por isso são mais facilmente polarizados e atraídos por campos elétricos externos.
R- B
15-(UFV-MG)
Saem da A e da C (positivas) e chegam a B (negativa) — R- E
16-(PUC-RS)
Os pontos devem estar equidistantes de Q — veja figura abaixo:
R- B
17-(UNIFESP-SP)
Todos os pontos de cada superfície equipotencial possuem o mesmo potencial elétrico — o trabalho realizado para levar a carga de um ponto ao outro independe da trajetória, dependendo apenas do potencial nos pontos inicial e final — W=q(VA – VB) — observe que a maior ddp (VA – VB) é a da trajetória V — R- E
18-(ITA-SP)
Kq1/d1 + Kq2/(6 – d1)=0 — K.1/d1 – K.2/(6 – d1)=0 — d1=2m — potencial é nulo a 2m de d1, ou seja,
nos pontos x=-4m e
x=4m e, em todos os pontos que constituem uma esfera de raio 4m (superfície equipotencial) —
R- A
19-(UFV-MG)
Blindagem eletrostática – Se, no interior de um condutor oco em equilíbrio eletrostático o campo elétrico
Esse fenômeno foi comprovado experimentalmente por Michael Faraday ao encerrar-se no interior de uma gaiola condutora, onde verificou não haver manifestação de fenômenos elétricos no seu interior. Essa gaiola deve ser feita de material condutor de eletricidade e não precisa ser contínua, podendo ser uma rede metálica, por isso recebeu o nome de gaiola.
A blindagem eletrostática (gaiola de Faraday) também é utilizada nos carros e aviões, oferecendo proteção contra descargas
elétricas. Construções também são feitas utilizando blindagem eletrostática, a fim de proteger seus equipamentos elétricos e eletrônicos.
R- D
20-(UFRGS)
Todo excesso de carga tenderá a repelir e ficarão concentrados na superfície da esfera externa —R- E
21-(UEG-GO)
Veja teoria em fisicaevestibular.com.br- eletricidade eletrostática- Condutor em equilíbrio eletrostático – Blindagem eletrostática — R- D
22-(UFMS-MS)
I. Correta — com S1 ligada, cargas elétricas negativas do gerador fluirão até a esfera condutora maciça eletrizando-a, que por sua vez induzirão cargas positivas na superfície externa da casca esférica condutora que também induzirão cargas no pêndulo, que continua neutro, atraindo-o por indução elétrica.
II. Correta — veja em fisicaevestibular o processo de eletrização por indução.
III. Falsa — a casca esférica eletrizada origina campo elétrico ao seu redor.
IV. Correta — veja 02
V. Falsa — veja 01
R- A