Electrodynamics – Equivalent Resistor in Series, Parallel and Mixed Associations – EN
ELECTRODYNAMICS – EQUIVALENT RESISTOR IN SERIES, PARALLEL AND MIXED ASSOCIATIONS
Electrodynamics
Equivalent Resistor in Series, Parallel and Mixed Associations
Exercises with ENEM characteristics
01-(UFMS-MS)

Equal electrical resistances (each with a value of 12 Ω) connect the vertices A, B and C of a triangle, as shown in the figure.
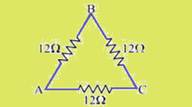
Regarding equivalent electrical resistance, it is correct to state that,
a) between vertices A and B, is 12 Ω
b) between vertices B and C, is 8Ω
c) between vertices A and C, is 36 Ω
d) between vertices A and B, is 24 Ω
e) between vertices A and B, is 36 Ω
02-(UESPI-PI)

The equivalent resistance between terminals A and B of the ideal battery in the following electrical circuit is equal to:
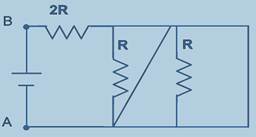
![]()
03-(MACKENZIE-SP)

The electrical resistance of the equivalent resistor of
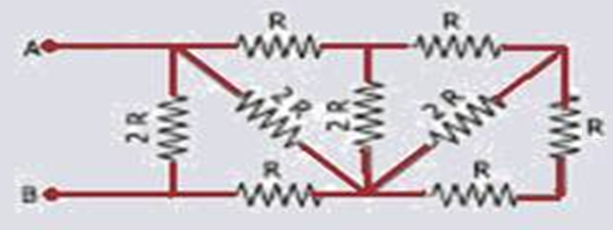
association below, between points A and B, is:
![]()
04-(PUC-SP)
For the circuit below, consider that all resistors are ohmic and of electrical resistance R.
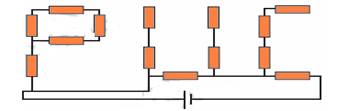
Calculate the value of the equivalent electrical resistance of the association.
![]()
05-(UF-PE)
In the circuit, what is the equivalent resistance between points A and B?
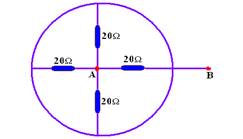
![]()
06-(FGV-SP)
Determine the resistance of the equivalent resistor of the combination below, between points x and y:
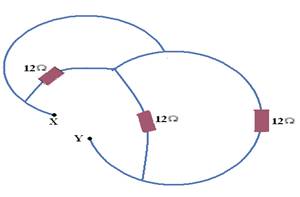
![]()
07-(FUVEST-SP)
A special conductive material becomes luminous when an electric current passes through it. Words were written on this material, and voltage sources were connected to terminals 1 and 2 in a dark room. The readable word is:

08-(UFRRJ-RJ)
The following figure shows a simple circuit that powers an electric shower C.
Among the following resistance systems, the one that will heat the water most quickly is:

09- (UNESP-SP)
As a result of the rapid development of electronic technology, it is now possible to carry out experiments in various areas of science using samples with dimensions of the order of nm (1 nm = 10 -9 m). New perspectives have been introduced and are being explored, such as investigations into the electrical properties of macromolecules and polymer chains, such as proteins.
Faced with this possibility, a researcher successfully verified his hypothesis that a certain protein, when stretched, satisfied Ohm’s law. After systematic measurements of its electrical resistance, he concluded that its value is R. Continuing his investigation, he divided this chain into two pieces, connecting them in parallel, and the effective resistance was measured to be 3R/16. Considering that the shorter piece has resistance R 1 and the longer piece has resistance R 2 , calculate these values expressed in terms of R.
a) R1 = R/4 and R2 = 3R/4
b) R1 = R/2 and R2 = 4R/3
c) R1 = 2R and R2 = 3R
d) R1 = R and R2 = 3R
e) R1 = R and R2 = 0
10- (CFT-MG)
FIG. 1 represents an association of identical resistors and FIG. 2, a battery and connecting wires.
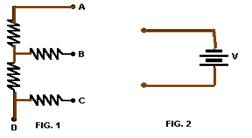
connection. To obtain the highest value of electric current, the wires must be connected at the points
![]()
