Eletrodinâmica – Primeira e Segunda lei de Ohm – Resolução

Resolução Comentada

Eletrodinâmica

Primeira e Segunda lei de Ohm

 

01-(ENEM-MEC)

Baseado nas  figuras:

(1) Mantendo-se a secção transversal constante e dobrando-se o comprimento (ℓ) do fi o, a resistência (R) dobra  —  então, a proporcionalidade entre ℓ e R é direta.

(2) Mantendo-se o comprimento constante e dobrando-se a área da secção transversal (A), a resistência (R) fica dividida por dois  —  então, a proporcionalidade entre A e R é inversa.

(3) Mantendo-se a resistência constante e dobrando-se o comprimento (ℓ) do fio, a área da secção transversal (A)

dobra. Assim, a proporcionalidade entre ℓ e A é direta.

R- C

 

02-UNESP-SP)

Para i=2 A  —  U=5.i2=5.22=5.4  —  U=20V  —  R=U/i=20/2  —  R=5 Ω  —  R- A

03-(UFG-GO)

 R=U/i  —  1.500=220/i  —  i=220/1.500  —  i=0,1466 A  —  i=146,6mA  —  R- D

 

04-(UFMS-MS)  

Verifique teoria a seguir: Primeira lei de Ohm – Se a resistência elétrica de um resistor for constante, a diferença de potencial aplicada nos seus extremos é diretamente proporcional à intensidade da corrente elétrica, ou seja,U₁/i₁=U₂/i₂= . . . =U/i=constante. Nesse caso eles são chamados de resistores (ou condutores) ôhmicos e, como a relação R=U/i é uma função do primeiro grau o gráfico U x i tem o aspecto do gráfico da esquerda da figura abaixo:

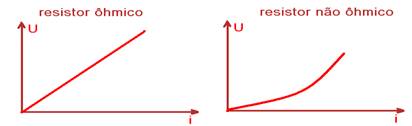
Qualquer gráfico U x i diferente do gráfico da esquerda da figura acima não representa um resistor ôhmico, como por exemplo, o gráfico da direita.

I- Falsa

II- Verdadeira

III- Falsa – veja cálculos abaixo

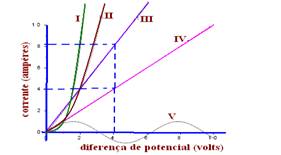
R_III=U/i=4/8=0,5Ω  —  R_IV=U/i=4/4=1Ω

 IV- Falsa – o condutor V não é ôhmico

V Falsa – acima de 1V, a resistência de I é a menor de todas as ôhmicas

R- A.

05-(CEFET-SC)

O chuveiro deve dissipar a mesma potência nos dois estados  —  P=U2/R  —  PSC=PPR  —   USC2/RSC= UPR2/RPR  —  USC=2UP­R  —  (2UPR)2/RSC= UPR2/RPR­  —  4UPR2/RSC= UPR2/RPR  —  RPR=RSC/4  —  R- C

 

06-(PUC-MG)

Água morna – média potência – resistência média  —  R- A

 

07-(UFAL-AL)

 Dados  —  U = 600 V  —   R1 = 2 kΩ = 2.103 Ω  —  R2 = 16 kΩ = 16.103 Ω  —  ao segurar as extremidades do peixe, a pessoa e o peixe se associam como resistores em série  —  aplicando a 1ª lei de Ohm  —  U = (R1 + R2) i  —  600 = 18 .10³ i  —  i = 600/18.10³  —  i=33,3.10^-3 A  —  i=33,3mA  —  19 mA < i < 100 mA  —   R- D

 

08-(FUVEST-SP) 

Observe o gráfico abaixo onde foram escolhidos dois pontos A e B: 

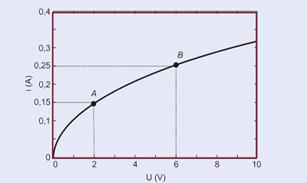
I. Falsa  —  quando a resistência é constante, tensão e corrente são diretamente proporcionais, portanto o gráfico é uma reta que passa pela origem.

II. Falsa  —  Calculando a resistência para os pontos, A e B, destacados na figura  —  R_A=U_A/i_A=2/0,15  —  R_A=13,3Ω  —  R_B=U_B/i_B  —  R_B=6/0,25  —  R_B=24Ω  —  a resistência aumenta com o aumento da corrente.

III. Correta  —   potências dissipadas para os valores dos pontos destacados  —  P_A = U_A. i_A = 2.(0,15) = 0,3 W  —  P_B=U_B.i_B  —  P_B=6.0,24=1,5W  —  P_B > P_A  —  a potência dissipada no filamento aumenta com o aumento da tensão aplicada. 

R- C

09-(PUC-MG)

Dados  —  D = 2 cm = 2.10^-2 m  —  L = 2.10³ m  —   i = 10³ A;  —   Δt = 1 h = 3,6.10³ s.

A resistência da linha é dada pela 2ª lei de Ohm  —  R=ρL/S  —   área da secção transversal  —   S= πr² =π(D/2)² —  S=πD²/4  —

R=ρL/S=4ρL/(πD²/4)=4(1,57.10^-8).(2.10³)/3,14.(2.10^-2)²  —  R=0,1Ω   —  P_o=R.i²  —  P_o=ΔW/Δt  —  ΔW=P_o.Δt  — 

ΔW=R.i².Δt  —  ΔW=0,1.(10³)².3,6.10³  —  ΔW=3,6.10⁸J.

R- A

 

10-(UNIFESP-SP)

Cálculo da resistência elétrica de cada fio  —  segunda lei de Ohm  —   R=ρL/S=1,6.10^-8.10/4.10^-6=1,6.10^-7/

4.10^-6  —  R=0,4.10^-1  —  R=0,04Ω  —  corrente que chega à residência  —  P_o=i.U  —  3.300=i.110  —  i=30 A  —  da caixa de relógio até a residência existem dois fios  —  R=2.0,04=8.10^-2Ω  —  P_o=R.i²=8.10^-2.900  —  P_o=72W  —  R- D.

 

11-(UDESC-SC)

Sendo R=ρ.L/S, pela tabela, o fio que possui menor resistência elétrica é o fio A  —  observe na expressão a seguir que, quanto maior a quantidade de energia consumida (W), maior será a potência dissipada (P_o) no fio  —  W=Po.Δt  —  observe também na expressão a seguir que  a potência elétrica dissipada no fio é inversamente proporcional à sua resistência elétrica R  —  Po=(U²/R).Δt  —  maior potência, menor resistência, consome mais energia  —  menor resistência – substituindo os valores de cada alternativa na equação R=ρ.L/S, chega-se à resposta  —  R- C

 

12-(UDESC-SC)

 I- Correta  —  P_o=R.i²  —  quanto maior i, maior P_o

II- Correta  —  R=ρL/S  —  quanto maior ρ, maior R e menor i

III- Falsa  —  é a razão U/i que é constante e não o produto U.i

IV- Correta  —  Falsa  —  depende do tipo de associação (série, paralelo ou mista)

R- D

 

Voltar para os exercícios